Frage58

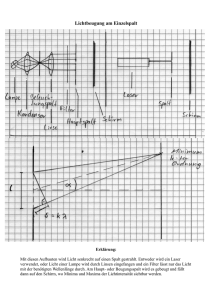
Themenbereich:
17 Welle-Teilchenproblematik, Phänomene der
Quantenphysik
Formeln:
𝑐
𝑓=𝜆
ℎ
𝜆=𝑝
(Louis de Broglie)
𝛥𝑥 ∗ 𝛥𝑝 ≥ ħ/2𝜋
𝛥𝐸 ∗ 𝛥𝑡 ≥ ħ/2𝜋
(Werner Heisenberg; ħ=h/2π)
FrNr:
58
f… Frequenz
c… Lichtgeschw.
λ… Wellenlänge
h… Plancksches
Wirkungsquantum
p… Impuls
x… Ort
E… Energie
t… Zeit
Wichtige Begriffe:
Beugung
Welle-Teilchen Dualismus
Heisenbergsche Unschärferelation
Wellenlänge
Wahrscheinlichkeitsfunktion als Lösung der Schrödingergleichung
Sonstige Anmerkungen:
Rechnen mit Wahrscheinlichkeiten anstatt mit exakten Werten (z.B. für einen
bestimmten Ort)
Ad a) Einzelspalt: Beugung erst möglich, wenn die Spaltbreite kleiner/gleich der
Wellenlänge λ ist; Wellenpaket: entsteht aus der Überlagerung mehrerer Wellen, die
beispielsweise den Impuls beschreiben (mehrere wegen der Unschärfe)
Ad b) Wäre es möglich, den Ort exakt zu wissen, wäre die Unschärfe gleich 0 – dann
wäre das Produkt aus Orts- und Impulsunschärfe auch 0 und somit nicht mehr größer
als ħ/2π! Es muss immer eine gewisse Unschärfe geben.
Ad c) Unschärferelation für Energie und Zeit, virtuelle Teilchen entstehen durch
Wechselwirkung der Teilchen außerhalb des leeren Raumes, kurze Zeit, hohe Energie
– damit der Energieerhaltungssatz nicht verletzt ist, muss ΔE*Δt kleiner (!) als ħ/2π
sein.
Ad d) Wie bei c muss ΔE*Δt kleiner oder gleich ħ/2π sein, man kann es ungefähr mit
ħ/2π abschätzen. E wird durch mc2 ersetzt, dann werden die Werte eingesetzt.
Bei d war meine Lösung immer 2,918*10-24s, in der Lösung des Beispiels ist die
Lösung mit 3*10-22s angegeben…
Katharina