Skalarprodukt Einführung

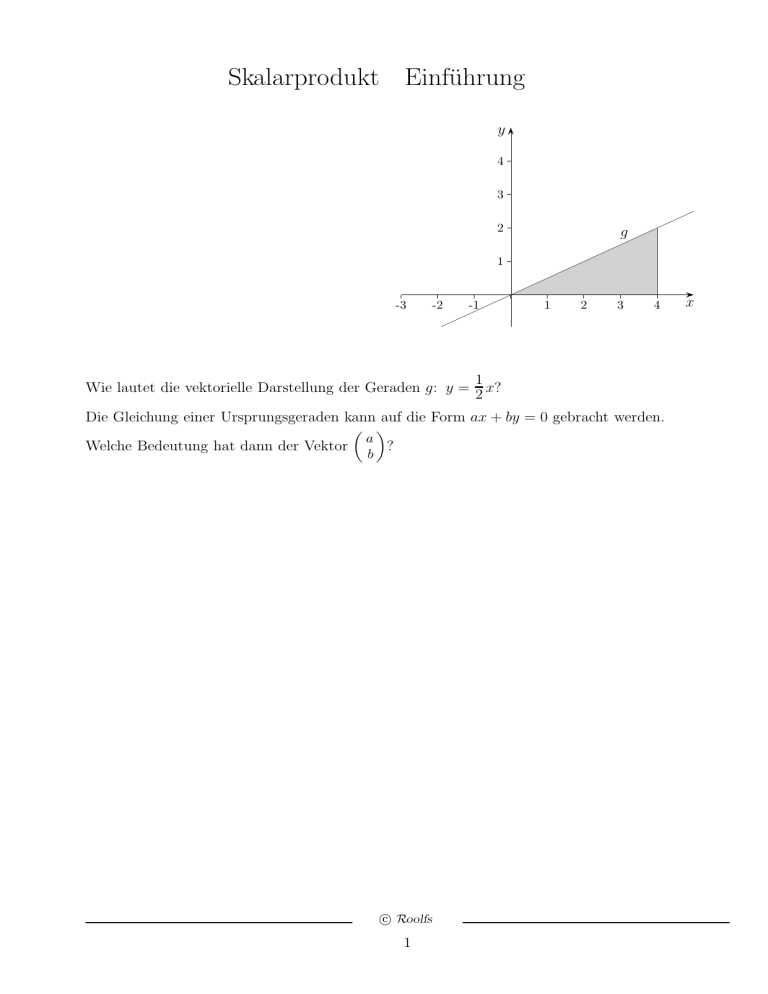
Skalarprodukt Einführung
y
4
3
2
g
1
-3
-2
-1
Wie lautet die vektorielle Darstellung der Geraden g: y =
1
2
3
4
1
x?
2
Die Gleichung einer Ursprungsgeraden kann auf die Form ax + by = 0 gebracht werden.
a
Welche Bedeutung hat dann der Vektor
?
b
c Roolfs
1
x
Skalarprodukt
y
3
−1
2
2
2
1
1
-3
g:
2
~x = λ
1
y=
1
x
2
⇐⇒
−x + 2y = 0
-2
-1
1
2
g
3
x
ax + by = 0
⇐⇒
a
−1
=
b
2
−1
2
2
⊥
1
Das eine Dreieck geht durch Drehung um 90◦ um den Ursprung aus dem anderen hervor.
−a
b
b
⊥
a
allgemeiner
−ra
rb
b
⊥
a
Mit der Definition des Skalarprodukts
a1
a2
b1
·
= a1 b1 + a2 b2
b2
erkennen wir:
~a ⊥ ~b
⇐⇒ ~a · ~b = 0
g kann durch
−1
x
−1
·
= 0 (Normalenform) beschrieben werden.
heißt Normalenvektor.
2
y
2
Welches geometrische Objekt wirdwohl
 durch x + 2y + z = 0 erfasst und
1
welche Bedeutung hat der Vektor  2 ?
1
c Roolfs
2
Ebene (z.B.)
x + 2y + z = 0
Um zu erkennen, dass die Lösungen der Gleichung x + 2y + z = 0 die Punkte einer Ebene
durch den Ursprung sind, stellen wir die Gleichung nach z um: z = −x − 2y
Für x = y = 0 erhalten wir z = 0. Wenn der x-Wert um 1 vergrößert wird,
verringert sich der z-Wert um 1, für x = 2 verringert sich der z-Wert um 2, usw.
Die Steigung in x-Achsenrichtung beträgt daher −1, und zwar unabhängig vom y-Wert.
In y-Achsenrichtung beträgt die Steigung −2.
z
6
5
4
3
-6
-5
2
-4
-3
1 -2
-1
-4
-3
-2
-1
1
1
2
-1
3
4
-2
5
6
-3
7
8
-4
9
10
-5
11
x
-6
-7
-8
c Roolfs
3
2
3
4
5
6
7
8
y