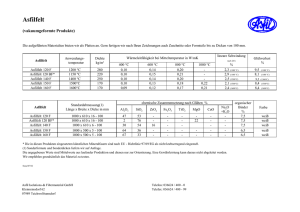
Betrachten Sie einen Monopolisten, der der einzige Produzent von

Betrachten Sie einen Monopolisten, der der einzige Produzent von Ingwerglühwein ist. Die
Grenzkosten für die Produktion eines Fasses dieses berühmten Glühweins betragen 40 Euro.
Die inverse Nachfragefunktion für diesen Wein ist
p=1600-q.
1. Betrachten Sie einen Einzelhändler, der der einzige Vertreiber dieses Weines ist. Er erhält den Wein direkt vom Produzenten, wobei keine Transportkosten anfallen.
a. Leiten Sie die Gewinnfunktionen für beide Unternehmen her.
Index P=Produzent und R=Einzelhändler
P = (w-40) * q
R = (1600-q) * q – w * q
b. Leiten Sie die optimale Mengen und den resultierenden Endverbraucherpreis in
Abhängigkeit vom Großhandelspreis her.
Das Problem wird durch Rückwärtsinduktion gelöst:1
∂R/∂q = 1600 – 2q - w = 0
 q*(w) = (1600 - w)/2
p*(w) = (1600 + w)/2
c.Berechnen Sie den optimalen Großhandelspreis.
P = (w - 40) (1600 - w) / 2)
dP/dw = (1600 - 2w + 40) /2 = 0

w * = 820
d. Berechnen Sie die optimale Mengen und den resultierenden Endverbraucherpreis.
q* = 390
p*(820) = (1600 + 820)/2 = 1210
e. Berechnen Sie den Gewinn für alle Unternehmen.
*P = 304.200
*R = 152.100
1
Da sowohl der Einzelhändler als auch der Produzent Monopolisten sind, ist es egal, ob der Einzelhändler den Ge-
winn nach der Menge oder nach dem Preis optimiert, das Ergebnis bleibt gleich. Dies gilt nur für diesen Spezialfall.
Prof. Dr. A. Sadrieh, Übung: Unternehmensinteraktion, WS 13/14
1
2. Betrachten Sie nun eine Situation in der zwei Einzelhändler den Glühwein vertreiben.
Diese beiden Einzelhändler stehen im Cournotwettbewerb und erhalten den Wein direkt
vom Produzenten. Auch hier fallen keine Transportkosten an.
a. Leiten Sie die Gewinnfunktionen für alle Unternehmen her.
P = (w-40) * (q1 + q2)
p = 1600 - Q und Q= q1 + q2
R1 = (1600 - q1 - q2)q1 – wq1
R2 = (1600 - q1 - q2)q2 – wq2
b. Leiten Sie die optimalen Mengen und den resultierenden Endverbraucherpreis in
Abhängigkeit vom Großhandelspreis her.
Rückwärtsinduktion:
Notwendige Bedingung:
∂R1/∂q1 = 1600 – 2q1 – q2 – w = 0
∂R2/∂q2 = 1600 – 2q2 – q1 – w = 0
Beste-Antwort-Funktion:
q1(q2) = (1600 – q2 – w )/2
q2(q1) = (1600 – q1 – w )/2.
Substitution führt zu:
q*1(w)= (1600 – w)/3
q*2 (w)= (1600 – w)/3
Gesamte Menge:
Q*(w) = (3200 – 2w)/3,
Resultierender Preis:
p*(w) = (1600 + 2w)/3
c. Berechnen Sie den optimalen Großhandelspreis.
P = (w-40) (3200 – 2w)/3
dP/dw = (3200 – 4w + 80) /3 = 0

w * = 820
d. Berechnen Sie die optimale Menge und den resultierenden Endverbraucherpreis.
p*(820) = (1600 + 1640)/3 = 1080
Q* = 520
e. Berechnen Sie den Gewinn für alle Unternehmen.
P = (820-40)520 = 405.600
R1 = R2 = (1080-820)260 = 67.600
Prof. Dr. A. Sadrieh, Übung: Unternehmensinteraktion, WS 13/14
2
3. Betrachten Sie nun den vertikal integrierten Fall, in dem der Produzent sein Produkt
ohne Einzelhändler direkt an den Endverbraucher verkauft. Leiten Sie den optimalen
Preis, die resultierende Menge und den Gewinn aller Marktteilnehmer her.
P = (w-40)(1600-w)
 w* = 820
Q* = 780
*P = 608.400
Das gleiche Ergebnis resultiert bei vollkommenem Wettbewerb unter den Einzelhändlern.
4. Vergleichen Sie die Ergebnisse aus Aufgaben 1-3.
Preise:
Der Produzent verlangt in allen Teilaufgaben den gleichen Preis (820). Der Preis, den
die Konsumenten zahlen, ist am niedrigsten im integrierten Fall, der gleich dem Fall
des vollkommenen Wettbewerbs unter den Einzelhändlern ist. Je stärker der Wettbewerb unter den Einzelhändlern ist, desto geringer ist der Endverbraucherpreis.
Mengen:
Mit steigendem Wettbewerb unter den Einzelhändlern steigt die Gesamtmenge die abgesetzt wird. Im Fall der vertikalen Integration ist die Gesamtmenge am größten.
Gewinne:
Der Monopolist hat den höchsten Gewinn, wenn er den Glühwein direkt vertreibt und
den niedrigsten Gewinn, wenn er über einen monopolistischen Einzelhändler vertreibt.
Je mehr Wettbewerb auf der Einzelhandelsebene herrscht, desto höher ist der Gewinn
des Produzenten. Bei vollkommenem Wettbewerb unter den Einzelhändlern erhält der
Produzent den höchsten Gewinn, der gleich dem Ergebnis bei vertikaler Integration ist.
Für einen Einzelhändler würde der Gewinn maximiert werden, wenn er der einzige Anbieter des Produktes ist. Je mehr Konkurrenz unter den Einzelhändlern herrscht, desto
geringer sind die Gewinne des einzelnen Einzelhändlers und die Summe der Gewinne
aller Einzelhändler.
Der Gesamtgewinn als Summe aller Einzelgewinne ist am höchsten bei vertikaler Integration und am niedrigsten in Fall 1.
Prof. Dr. A. Sadrieh, Übung: Unternehmensinteraktion, WS 13/14
3