Fehlerwahrscheinlichkeiten

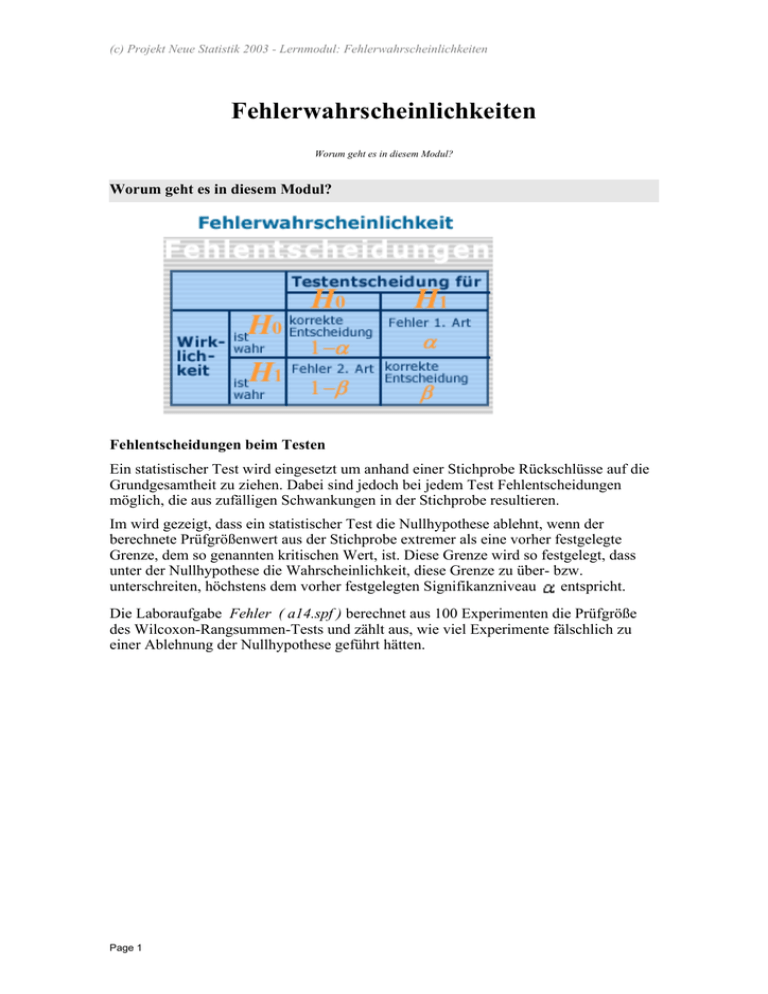
(c) Projekt Neue Statistik 2003 - Lernmodul: Fehlerwahrscheinlichkeiten
Fehlerwahrscheinlichkeiten
Worum geht es in diesem Modul?
Worum geht es in diesem Modul?
Fehlentscheidungen beim Testen
Ein statistischer Test wird eingesetzt um anhand einer Stichprobe Rückschlüsse auf die
Grundgesamtheit zu ziehen. Dabei sind jedoch bei jedem Test Fehlentscheidungen
möglich, die aus zufälligen Schwankungen in der Stichprobe resultieren.
Im wird gezeigt, dass ein statistischer Test die Nullhypothese ablehnt, wenn der
berechnete Prüfgrößenwert aus der Stichprobe extremer als eine vorher festgelegte
Grenze, dem so genannten kritischen Wert, ist. Diese Grenze wird so festgelegt, dass
unter der Nullhypothese die Wahrscheinlichkeit, diese Grenze zu über- bzw.
unterschreiten, höchstens dem vorher festgelegten Signifikanzniveau
entspricht.
Die Laboraufgabe Fehler ( a14.spf ) berechnet aus 100 Experimenten die Prüfgröße
des Wilcoxon-Rangsummen-Tests und zählt aus, wie viel Experimente fälschlich zu
einer Ablehnung der Nullhypothese geführt hätten.
Page 1
(c) Projekt Neue Statistik 2003 - Lernmodul: Fehlerwahrscheinlichkeiten
Drei Prüfgrößenwerte überschreiten den kritischen Wert, der in der Grafik als roter Strich dargestellt ist.
Verwirft der Test aufgrund eines extremen Prüfgrößenwertes die Nullhypothese,
obwohl diese wahr ist, wird ein Fehler bei der Testentscheidung begangen. Dieser
Fehler wird der Fehler 1. Art genannt.
Fehler 1. Art
Der Fehler 1. Art tritt auf, wenn
abgelehnt wird, obwohl
wahr ist.
Ein zweiter möglicher Fehler wird begangen, wenn an der Nullhypothese irrtümlich
festgehalten wird.
Fehler 2. Art
Der Fehler 2. Art tritt auf, wenn
beibehalten wird, obwohl
wahr ist.
Damit, wie in der folgenden Tabelle zusammengefasst, kann bei einem statistischen
Test einer von vier möglichen Ausgängen eintreten:
Nach Durchführung eines statistischen Tests kann jedoch nicht beurteilt werden, ob
dieser ein falsches oder ein korrektes Ergebnis geliefert hat. Es müsste daher versucht
Page 2
(c) Projekt Neue Statistik 2003 - Lernmodul: Fehlerwahrscheinlichkeiten
werden, zumindest die Wahrscheinlichkeit für ein fehlerhaftes Testergebnis
abzuschätzen oder zu begrenzen.
Fehler 1. Art
Im Beispiel für den Wilcoxon-Test haben wir gesehen, dass ein statistischer Test so
konstruiert ist, dass die Nullhypothese verworfen wird, wenn mit einer
Wahrscheinlichkeit von höchstens
die Prüfgröße den zugehörigen kritischen Wert
über- bzw. unterschreitet, also falls
Diesem Vorgehen liegt die Idee zugrunde, dass das Eintreten eines Ereignisses, das mit
so kleiner Wahrscheinlichkeit unter der Verteilung der Nullhypothese eintritt, eher die
Verteilung unter der Alternative verantwortlich ist. Bei der dann zutreffenden
Entscheidung für
wird gerade diese Wahrscheinlichkeit als Restrisiko für eine
Fehlentscheidung in Kauf genommen.
Also: Wenn der Fehler 1. Art auftritt, hat man sich für
entschieden, obwohl
wahr ist. Unter einer wahren Nullhypothese entscheidet sich der Test aber nur mit einer
Wahrscheinlichkeit von höchstens
fälschlicherweise für die Alternative.
Das Signifikanzniveau
ist die Wahrscheinlichkeit, die Nullhypothese fälschlich zu
verwerfen;
wird deswegen auch Irrtumswahrscheinlichkeit genannt. Der Fehler 1.
Art wird also durch das Signifikanzniveau
kontrolliert, da
vor jeder
Testdurchführung festgelegt werden muss. Ein statistischer Test, bei dem der Fehler 1.
Art kontrolliert wird, heißt Signifikanztest, d.h. falls für
gilt:
Signifikanztest
Wichtig ist dabei, dass diese Wahrscheinlichkeit unter der Annahme berechnet wird,
dass
zuträfe. D.h. die Daten müssen sich gegen diese Annahme durchsetzen, also
sehr deutlich für die Alternative sprechen. In diesem Sinne wird die Rolle der
Nullhypothese auch oft mit der eines Advocatus Diaboli verglichen (vgl. Beispiel).
Fehler 2. Art
Die Wahrscheinlichkeit für den Fehler 2. Art wird mit
bezeichnet. Im
Gegensatz zum Fehler 1. Art wird der Fehler 2. Art nicht durch eine vorgegebene
Schranke kontrolliert. Es ist leider nicht möglich, beide Fehlerarten gleichzeitig zu
minimieren. Daher wird versucht, unter allen Signifikanztests (Tests, die den F.1.A.
kontrollieren) denjenigen zu finden, der die Fehlerwahrscheinlichkeit
minimiert. Unter Umständen kann die Wahrscheinlichkeit für den Fehler 2. Art
allerdings sehr groß werden. Für den Fall, dass der statistische Test sich für
Page 3
(c) Projekt Neue Statistik 2003 - Lernmodul: Fehlerwahrscheinlichkeiten
sprechen oder gar davon, dass sie statistisch bewiesen ist. Man kann lediglich davon
ausgehen, dass es nicht gelungen ist, zu widerlegen. Das Prinzip, das hier dem Test
zugrunde liegt, findet sich auch in der Philosophie, und zwar im dem Popperschen
Falsifizierbarkeitsprinzip (Sir Karl S. Popper, 1902-1994. ).
Eng verbunden mit dem Fehler 2. Art ist der Powerbegriff (siehe dazu das ).
Wir wollen das statistische Testprinzip in anderen Kontexten veranschaulichen und
betrachten dafür die folgenden zwei Beispiele und eine Laborsimulation
Beispiel: Entscheidungsproblem eines Richters
Betrachten Sie sich noch einmal das Beispiel 4 (Rechtssprechung in einem Mordfall)
aus dem
In der deutschen Rechtssprechung wird nach dem Vorsatz "in dubio pro reo" (im
Zweifel für den Angeklagten) verfahren. Daher kann der judizielle Gedanke
folgendermaßen in Hypothesen formuliert werden:
Der Angeklagte ist unschuldig gegen
Der Angeklagte ist schuldig.
D.h. nur bei ausreichender Beweislast wird der Angeklagte für schuldig gesprochen,
also die Nullhypothese verworfen. Die Fehlerwahrscheinlichkeiten sind hier
folgendermaßen zu interpretieren:
Fehler 1. Art
Der Richter verurteilt den Angeklagten, obwohl dieser unschuldig ist, d.h. er hat
abgelehnt, obwohl wahr ist.
Fehler 2. Art
Der Richter begeht den Fehler 2. Art, wenn der wirkliche Mörder auf der Anklagebank
sitzt, er ihn aber z.B. wegen fehlender Beweise nicht verurteilt.
Der Richter hat sich dann für
entschieden, obwohl
wahr ist.
Zusammenfassend können folgende Ereignisse eintreten:
Beide Fehlerarten können nur deshalb auftreten, da der Richter die Wirklichkeit nicht
kennt. Er muss anhand des vorliegenden "Datenmaterials" (z.B. Zeugenaussagen, Fotos,
Rekonstruktionen, ...) das bestmöglichste Urteil fällen. Bei einem statistischen Test ist
das ähnlich: Die Grundgesamtheit und auch die wahren Parameterwerte sind unbekannt.
Nach einem Testentscheid kann auch nicht beurteilt werden, ob dieser richtig oder
falsch ist. Im Gegensatz zu einem richterlichen Urteilsspruch bietet ein statistischer Test
jedoch einen entscheidenden Vorteil: Der Fehler 1. Art wird durch das
Signifikanzniveau kontrolliert.
Beispiel: Produzenten- und Konsumentenrisiko
Der Hersteller eines Produkts stellt die Nullhypothese auf, dass der Anteil defekter
Page 4
(c) Projekt Neue Statistik 2003 - Lernmodul: Fehlerwahrscheinlichkeiten
Stücke in der Produktionsserie höchstens 4% beträgt (siehe Beispiel im ).
Nehmen wir an, auf der Basis einer Stichprobe wird die Nullhypothese abgelehnt,
obwohl in der gesamten Produktion der Ausschussanteil wirklich unter 4 % liegt, so
haben wir es mit dem Fehler 1. Art zu tun. Er entspricht dem Produzentenrisiko.
Nehmen wir andererseits an, dass auf der Basis einer Stichprobe die Hypothese nicht
abgelehnt wird, obwohl der Ausschussanteil in der gesamten Produktion über 4% liegt,
so haben wir es mit dem Fehler 2. Art zu tun. Er entspricht dem Konsumentenrisiko.
Welcher Fehler, der Fehler 1. Art oder der Fehler 2. Art, stärker ins Gewicht fällt, hängt
natürlich ganz wesentlich von der Behauptung (Hypothese) und den Folgen der
Entscheidung ab. Im Beispiel 2 kann man geteilter Meinung sein, ob das
Produzentenrisiko oder das Konsumentenrisiko höher zu bewerten ist. Produzent und
Konsument werden wohl jeweils ihr eigenes Risiko für gravierender halten. Im ersten
Beispiel ist die Bedeutsamkeit der Fehler unterschiedlich zu bemessen. Um die
persönlichen Freiheitsrechte eines jeden Bürgers zu wahren, ist die potenzielle
Nichtverurteilung eines Mörders eher zu rechtfertigen (Fehler 2. Art), als dass ein
Unschuldiger zu lebenslanger Haft verurteilt wird (Fehler 1. Art).
Beispiel: Simulationsbeispiel
Starten Sie die Simulation Fehlerwahrscheinlichkeiten ( ae3.spf ) im Statistiklabor.
Es sollen die Fehlerwahrscheinlichkeiten an folgendem Testproblem simuliert werden:
gegen
Dazu generieren wir uns unter wahrer Nullhypothese (die Verteilungen beider
Grundgesamtheiten, aus denen die Stichproben gezogen werden, sind gleich) 100
Stichproben mit je 10 Beobachtungen und berechnen mit Hilfe des
Wilcoxon-Rangsummen-Tests den Prüfgrößenwert.
Simultan werden unter wahrere Alternativhypothese (die Verteilungen der
Grundgesamtheiten, aus denen die Stichproben gezogen werden, unterscheiden sich
hinsichtlich ihrer Lage) 100 Stichproben mit je 10 Beobachtungen simuliert und der
jeweilige Prüfgrößenwert berechnet.
Die Prüfgrößenwerte, die unter der wahren Nullhypothese generiert wurden, sind blau dargestellt. Prüfgrößenwerte, die unter der
wahren Alternative simuliert wurden, sind rot. Es ist ersichtlich, dass die Verteilung von Null- und Alternativhypothese sich in der
Lage unterscheiden. Aber wie groß muss der Prüfwert (x-Achse) sein, damit man sich für einen Lageunterschied entscheidet (d.h.
Entscheidung für die Alternative), wenn wir höchstens eine Fehlerwahrscheinlichkeit für den Fehler 1. Art von 5% dulden wollen?
Im Kapitel Idee des Testens wurde gezeigt, dass ein statistischer Test sich für das
Verwerfen der Nullhypothese entscheidet, wenn der Prüfgrößenwert extremer ist als
eine vorher festgelegte Grenze (den oder die kritische(n) Wert(e)).
A) Geben Sie sich ein Signifikanzniveau vor, und legen Sie in der Simulationsaufgabe
willkürlich eine Grenze fest.
Zählen Sie, wie viele Prüfgrößenwerte aus der wahren Nullhypothese und aus der
wahren Alternativhypothese extremer sind.
Wiederholen Sie die Simulationen mehrere Male, und beobachten Sie, wie sich die
Ergebnisse ändern.
B) Berechnen Sie, wie viele Prüfwerte unter der wahren Nullhypothese fälschlich
abgelehnt werden (Fehler 1. Art) und wie viele Prüfwerte unter der wahren Alternative
nicht abgelehnt (Fehler 2. Art) werden.
Page 5
(c) Projekt Neue Statistik 2003 - Lernmodul: Fehlerwahrscheinlichkeiten
Interpretieren Sie die Fehlerwahrscheinlichkeiten.
C) Verändern Sie den Lageunterschied der Grundgesamtheiten, indem Sie die
Mittelwerte (mux oder muy) in folgendem Aufruf verändern.
> simul(100,mux=1,muy=1.2)
D) Verändern Sie die Anzahl der Beobachtungen innerhalb der gezogenen Stichproben
mit dem Argument s:
> simul(100,s=100,mux=1,muy=2)
Eine Lösung finden Sie hier: Lösungsdatei öffnen ( b03.spf )
Ein neues Medikament zur Blutdrucksenkung soll auf den Markt gebracht werden.
Dazu soll nachgewiesen werden, dass es nicht schlechter als ein bereits erhältliches
Präparat wirkt.
Versuchen Sie das inhaltliche Problem als statistisches Testproblem zu quantifizieren.
Was bedeuten hier der Fehler 1. und 2. Art?
Quelle:
Ein Schokoladenliebhaber hat den Verdacht, dass das Gewicht seiner
Lieblingsschokolade weniger geworden ist. Früher hat die Tafel durchschnittlich 100g
gewogen.
Schreiben Sie das Testproblem auf, und interpretieren Sie den Fehler 1. und 2. Art aus
der Sicht des Schokoladenliebhabers.
Quelle:
Der Schokoladenliebhaber aus Aufgabe "Schokolade (1)" hat empört die
Herstellerfirma seiner Lieblingsschokolade angeschrieben. Die Firma möchte den
Verdacht, ihre Tafeln wären leichter geworden, nicht auf sich sitzen lassen. Die Firma
behauptet sogar, dass genau das Gegenteil der Fall ist: Die Tafeln sind im Laufe der
Zeit schwerer geworden!
Stellen Sie das Testproblem auf und interpretieren Sie die Fehlerwahrscheinlichkeiten.
In einer Produktionsstätte werden Bremsseile mit einer bestimmten Zugkraft produziert,
die an Motorradhersteller verkauft werden. Um die Qualität zu gewährleisten, wird in
regelmäßigen Abständen eine Stichprobe gezogen und getestet, bei wie viel Belastung
die Seile reißen. Gegebenfalls wird die Einstellung an den Maschinen korrigiert.
Formulieren Sie den Sachverhalt als Testproblem, und geben Sie inhaltlich den Fehler
1. und 2. Art an. Welche Fehlerart möchte der Produzent und welche Fehlerart möchte
der Konsument minimieren?
Eine intakte Motorradbremse!
Quelle:
Lösung Medikamente
Page 6
(c) Projekt Neue Statistik 2003 - Lernmodul: Fehlerwahrscheinlichkeiten
= Blutdrucksenkung mit neuem Medikament; = Blutdrucksenkung mit altem
Medikament
gegen
Fehler 1. Art (H0 verwerfen, obwohl wahr)
Das neue Medikament wird zugelassen, obwohl es nicht besser wirkt.
Fehler 2. Art (H0 beibehalten, obwohl falsch)
Obwohl das neue Medikament besser ist als das bereits bestehende Präparat, bekommt
es keine Zulassung
Lösung Schokolade (1)
H0: Gewicht der Tafeln >= 100
H1: Gewicht der Tafeln < 100
Fehler 1. Art (H0 verwerfen, obwohl wahr)
Der Verdacht gegen seine Produktionsfirma seiner Lieblingsschokolade wurde bestätigt,
obwohl in Wahrheit die Tafeln nicht leichter als 100g sind.
Fehler 2. Art (H0 beibehalten, obwohl falsch)
Der Verdacht, dass die Schokoladentafeln leichter geworden sind, wurde nicht bestätigt,
obwohl die Tafeln in Wahrheit leichter als 100g sind.
Lösung Schokolade (2)
H0: Gewicht der Tafeln <= 100
H1: Gewicht der Tafeln > 100
Fehler 1. Art (H0 verwerfen, obwohl wahr)
Aufgrund der Testentscheidung kann die Firma behaupten, Tafeln mit größerem
Gewicht hergestellt zu haben, obwohl die Tafeln in Wahrheit leichter als 100g sind.
Fehler 2. Art (H0 beibehalten, obwohl falsch)
Aufgrund der Testentscheidung kann die Firma nicht beweisen, dass ihre Tafeln
schwerer als 100g sind, obwohl sie es in Wahrheit sind.
Lösung Bremsseil
gegen
Fehler 1. Art (Produzentenrisiko)
Das Los wird nicht angenommen, obwohl die Seile in Ordnung sind. Das hat eine zeitund kostenintensive Adjustierung der Maschinen zur Folge.
Die Wahrscheinlichkeit für den Fehler 1. Art möchte der Produzent minimieren.
Fehler 2. Art (Konsumentenrisiko)
Das Los wird angenommen, obwohl die Seile nicht die erforderliche Reißkraft
aufweisen. Dies könnte im schlimmsten Fall schwere Unfälle bei den Motorradfahrern
verursachen.
Page 7
(c) Projekt Neue Statistik 2003 - Lernmodul: Fehlerwahrscheinlichkeiten
Falsifizierbarkeitsprinzip
ErklärungFehlentscheidung
ErklärungFehler 1. Art
ErklärungFehler 2. Art
ErklärungIrrtumswahrscheinlichkeit
ErklärungKonsumentenrisiko
ErklärungProduzentenrisiko
ErklärungSignifikanztest
ErklärungWahrscheinlichkeit für den Fehler 2. Art
Erklärung
(c) Projekt Neue Statistik 2003, Freie Universität Berlin, Center für Digitale Systeme
Kontakt: http://www.neuestatistik.de
Page 8