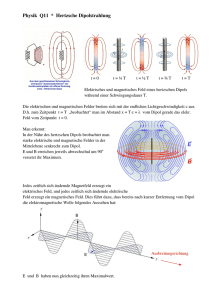
Kein Folientitel

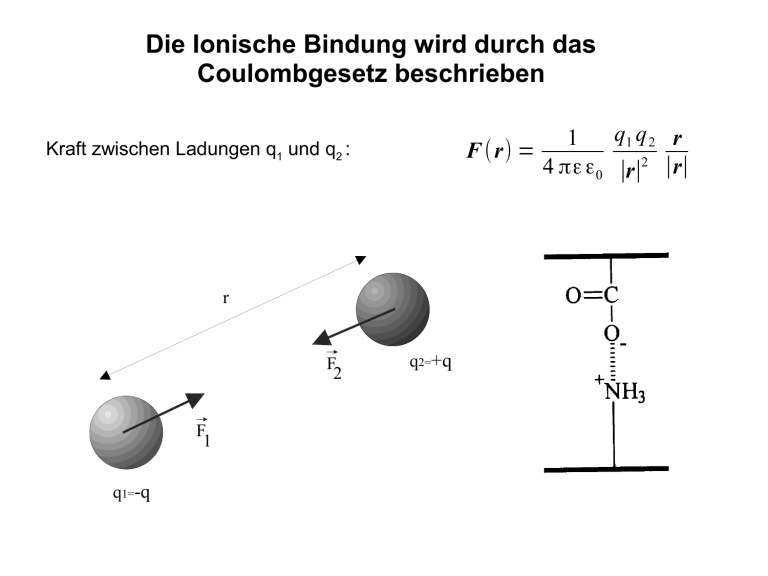
Die Ionische Bindung wird durch das
Coulombgesetz beschrieben
q1 q 2 r
1
F (r) =
4 πε ε0 ∣r∣2 ∣r∣
Kraft zwischen Ladungen q1 und q2 :
r
F
2
F
1
q1=-q
q2=+q
Berechnung der Bindungsenergie
r ' =∞
r ' =∞
E ( r) = ∫r ' =r F (r ' ) dr ' = ∫r ' =r
q1 q 2
q1 q 2
1
1
dr ' =
2
4 π εε 0 r '
4 π ε ε0 r
Der polare Charakter des Wassers: Ein Molekül
mit einem elektrischen Dipol
l
q-
q+
p

pH2O  6.17  10 30 Cm
Elektrisches
Dipolmoment:
p =∣q∣ l
n
p ges = ∑i =1 p i
Das Dipolmoment des Wassers ermöglicht die
Hydratisierung von Ionen und Proteinen mit polaren
Gruppen auf der Oberfläche
Auch polare Proteine
sind hydratisiert
Elektrisches Feld eines Dipols
3u r ( p⋅ur )− p
1
E (r) =
3
4 πε ε0
∣r∣
gültig nur im größeren
Abstand vom Dipol:
∣r∣ ≫ ∣l∣
Elektrisches Feld eines Dipols
(gültig nur im größeren Abstand vom Dipol)
3u r ( p⋅ur )− p
1
E (r) =
4 πε ε0
∣r∣3

Potentielle Energie eines Dipols im elektrischen Feld E
E p = − p⋅E
Bindungsenergie zwischen zwei Dipolen
p1⋅p 2−3(u r⋅p 1)(ur⋅p2 )
1
E p (r ) =
4 π εε 0
∣r∣3
p1 p 2 K 1
E p (r ) =
4 π ε ε0 ∣r∣3
K = sin θ 1 sin θ 2 cos(Φ1−Φ2 ) − 2cos θ1 cos θ 2
Induzierte elektrische Dipole sind die Ursache
für die van-der-Waals Wechselwirkung
p = α ε0 E
: Polarisierbarkeit
E
[]=m3
E
E p = −∫0 p⋅d E ' = −α ε0∫0 E '⋅d E ' =
E
= −α ε0 ∫0
1
2
u E⋅u E ∣E '∣dE ' = − α ϵ0∣E∣
2
2
Quantenmechanische Betrachtung:
3h να
E p (r ) = −
4 π2 r 6
h = 6.626  10-34 Js
Ein empirisches Potential für die van der Waals
Wechselwirkung: Das Lenard-Jones-Potential
6
  r0 12

r


0
ELJ (r )  E0     2  
 r 

r




E/E0 6
E LJ /E 0
4
r=r 0
2
0
-2
0
r/r 0
2
Abstandsabhängigkeit der potentiellen Energie
zwischen statischen und dynamischen Ladungsverteilung
Ion
Ion
~
Dipol
induzierter Dipol
1  1
~ 
r  r
Dipol
induzierter Dipol
~
1  1
~ 
r2  r 4 
~
1  1
~ 
r4  r4 
~
1  1
~ 
r3  r6 
~
1  1
~ 
r6  r6 
~
1  1
~ 6
6 
r  r 
*bei Brownscher Molekularbewegung gelten die
Ausdrücke in Klammern
Wasserstoffbrückenbindungen
Eis
Flüssiges Wasser
Nichtpolare Moleküle gehen keine
Wasserstoffbrückenbindungen ein und werden von
einer Wasserhülle eingeschlossen.
Wasserstoffbrückenbindungen stabilisieren
Proteinstrukturen
Wasserstoffbrückenbindungen stabilisieren
Proteinstrukturen
-Helix
Paralleles
Anti-paralleles
-Faltblatt
-Faltblatt
Empirisches Potential für Wasserstoffbrückenbindung
(10-12 Lennard-Jones-Potential)
A
B
E WB (r ) = 12 − 10
r
r
A, B:
Für die jeweilige Wasserstoffbrückenbindung zu bestimmende Konstanten
Typische Abstände:
F - H ··· F
2.25 Å
O - H ··· O
2.90 – 3.00 Å
N - H ··· N
2.90 – 3.00 Å
Die Polypeptidkette wird durch kovalente
Bindungen zusammengehalten
Die sechs Atome C-CONH-C liegen in einer
Ebene.
Die Aminosäurekette ist nur an den CAtomen um die Winkel  und  drehbar.
Empirisches Federpotential
E p ,1 (r ) = K 1 (r−r 0 )2
r0 :
Gleichgewichtsabstand
K1 :
Kraftkonstante
Bond type
r0 (pm)
K1 (J mol-1 pm-2)
C-C
150,7
132
C=C
133,6
239
C-N
144,9
141
C=N
127,3
239
Empirisches Potential für Bindungswinkel
2
E p ,2 (r ) = K 2 (θ−θ0 )
0 :
Gleichgewichtswinkel
K2 :
Kraftkonstante
Winkel
0 (Grad)
K2 (J mol-1 rad-2)
C-C-C
112,4
264
C-N-C
121,9
209
Torsionspotential
V
E p ,3 = [1+cos (n θT −γ)]
2
T: Torsionwinkel, V: Energiebarriere für Rotation,
n: Anzahl von Rotationsisomeren, : Phase
Beispiel für zwei C-Atome in der Kette X - C – C – X:
n = 4,  = 0 und V = 16 kJ mol-1
Größenordnungen von Bindungsenergien
Kovalente Bindung:
Ionische Bindung :
200-500 kJ mol-1
10-30 kJ mol-1
(berechnet für 1mM NaCl in H2O)
Wasserstoffbrückenbindung:
van-der-Waals Bindung:
10-30 kJ mol-1
1-4 kJ mol-1
Proteindynamik
Bewegung von Proteinen ist wesentlich komplizierter als die Dynamik
von kleinen Molekülen wie z.B. CO und H2O
Normalschwingungen von CO
 in s-1
Normalschwingungen von H2O
Hooksches Gesetz in einer Dimension
F  Dx
F:
Kraft
(SI-Einheit: N)
D:
Kraftkonstante
(SI-Einheit: N m-1)
x:
Auslenkung aus der Ruhelage (SI-Einheit: m)
Hooksches Gesetz in 9 Dimensionen
(für die 9 kartesischen Koordinaten von H2O)
F  Dx
 x1 
 
 x2 
x 
 3
 x4 
x   x5 ,
 x6 
 
 x7 
 x8 
 
 x9 
 F1 
 
 F2 
F 
 3
 F4 
F   F5 ,
 F6 
 
 F7 
 F8 
 
 F9 
Koordinatenvektor
Kraftvektor
 D1,1

 D2,1
 ⋮

 ⋮

D ⋮
 ⋮

 ⋮
 ⋮

 D9,1
D1, 2
D2, 2
⋮
⋮
⋮
⋮
⋮
⋮
D9, 2
⋯ ⋯ ⋯ ⋯ ⋯ ⋯ D1,9 

⋯ ⋯ ⋯ ⋯ ⋯ ⋯ D2,9 
⋱
⋮ 

⋱
⋮ 
⋱
⋮ 
⋱
⋮ 

⋱
⋮ 
⋱
⋮ 

⋯ ⋯ ⋯ ⋯ ⋯ ⋯ D9,9 
Kraftkonstantenmatrix
Kraftkonstantenmatrix für H2O
872.4
D=
0.0
0.2
-174.6
0.0
961.4
-70.9
0.0
-54.9
77.7
0.0
-0.1
0.0
0.0
0.1
41.1
0.0
-846.0
-27.0
0.0
870.2
-801.5
0.0
228.5
-6.8
0.0
-14.2
808.3
0.0
-0.1
0.0
0.0
0.0
0.0
0.0
0.1
132.5
0.0
-115.4
81.9
0.0
-24.2
-214.3
0.0
139.6
Kraftkonstantenmatrix für H2O im Hauptachsensystem
0
0
0
0
D=
0
0
176.0
933.8
1016.5
Allgemein: Eigenwerte der Kraftkonstantenmatrix
für nicht-lineare Moleküle
3 Eigenwerte gleich Null für Translationen des gesamten
Moleküls
3 Eigenwerte gleich Null für Rotationen des Moleküls
3N-6 Eigenwerte ungleich Null für Molekülschwingungen
(N : Anzahl der Atome im Molekül)