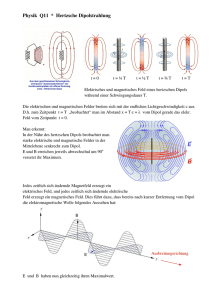
4.3.2 Potential eines Dipols im Dipolfeld • Gesamtpotential ist

4.3.2
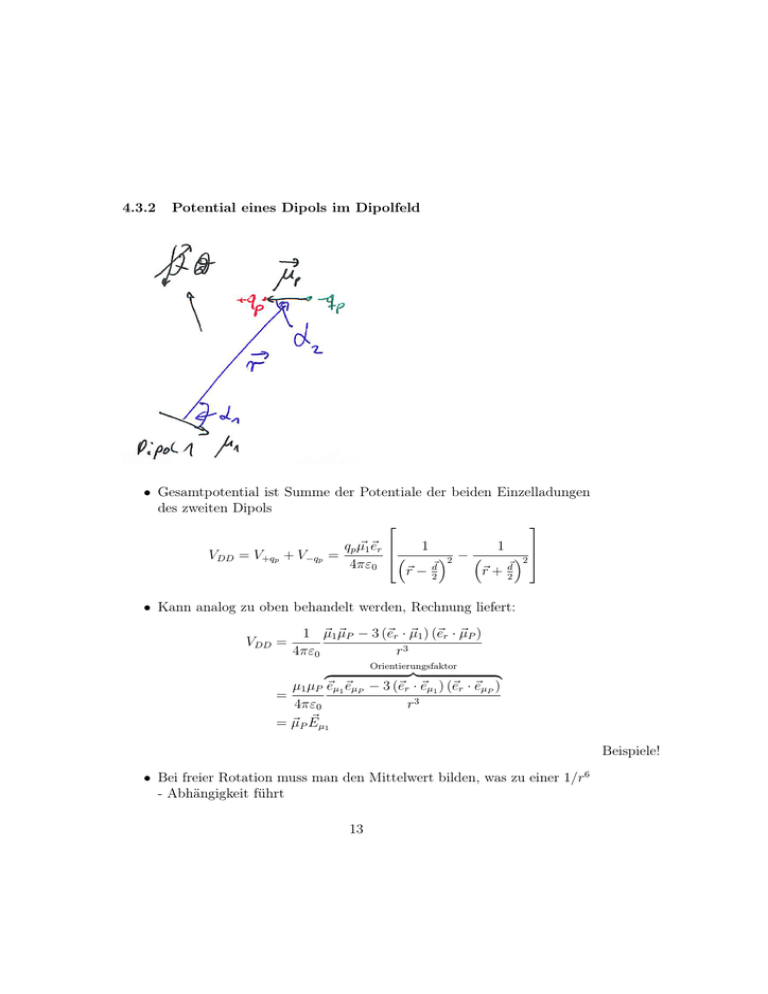
Potential eines Dipols im Dipolfeld
• Gesamtpotential ist Summe der Potentiale der beiden Einzelladungen
des zweiten Dipols
2
3
VDD = V+qp + V
qp
=
qp µ~1~er 6
1
4⇣
⌘
~ 2
4⇡"0
~r d2
1
7
⇣
⌘2 5
~
~r + d2
• Kann analog zu oben behandelt werden, Rechnung liefert:
VDD =
1 µ
~ 1µ
~P
4⇡"0
z
µ1 µP ~eµ1 ~eµP
=
4⇡"0
~ µ1
=µ
~P E
3 (~er · µ
~ 1 ) (~er · µ
~P )
r3
Orientierungsfaktor
}|
{
3 (~er · ~eµ1 ) (~er · ~eµP )
r3
Beispiele!
• Bei freier Rotation muss man den Mittelwert bilden, was zu einer 1/r6
- Abhängigkeit führt
13
4.3.3
Potential Dipol und Influenzierter Dipol
• Jedes Atom ist polarisierbar (Verschiebung der Ladungsdichteverteilung der Elektronen gegen den Kern)
• influenzierter (induzierter) Dipol im elektrischen Feld:
~
µ
~ = ↵"o E
• Damit kann man die Wechselwirkungsenergie (Potential) des influenzierten Dipols im Dipolfeld bestimmen
• Wir wollen hier die exakte Form gar nicht betrachten, nur die Abhängigkeit vom Abstand r
V DDi =
4.3.4
~ =
µ·E
~E
~ =
↵"0 E
↵"0 |E|2 / 1/r6
Sich gegenseitig influenzierende Dipole
• Quantenmechanisch kann man zeigen, dass sich zwei Atome gegenseitig
influenzieren können !Von-der-Waals-Anziehung
• Das Lennart-Jones Potential besteht aus einem Van-der-Waals-Anziehungsterm
und einem Abstoßungsterm
• Abstoßung ist Quadrat des Anziehungsterms (weil es sich so schön einfach rechnet)
VLJ (r) = V0
4.3.5
✓⇣
ro ⌘12
r
2
⇣ r ⌘6 ◆
o
r
Wasserstoffbrückenbindung
• allgemein akzeptierter analytischer Ausdruck noch nicht gefunden
• trotz gerichteten Charakters oft als Zentralpotential genähert der Form
VHH = Ar
14
12
Br
10