2.1 Elektrisches Potential

2.1
Elektrisches Potential
• Potentielle Energie zweier Punktladungen
Z r
Q1 Q2
Q1 Q2 r
Q1 Q2
VC =
dr =
|1 =
2
4⇡✏✏o r
4⇡✏✏o r
1 4⇡✏✏o r
• Elektrisches Potential ist der Quotient aus potentieller Energie und
einer Ladung
=
Vc =
Vc
Q1
=
Q2
4⇡✏✏o r
Q1 Q2
1
p
2
4⇡✏✏o x + y 2 + z 2
Fx =
@V
=
@x
1 Q1 Q2
2x
2
2 4⇡✏✏o (x + y 2 + z 2 ) 32
Fy =
@V
=
@y
1 Q1 Q2
2y
2
2 4⇡✏✏o (x + y 2 + z 2 ) 32
@Fx
3 Q1 Q2
2yx
=
2
@y
2 4⇡✏✏o (x + y 2 + z 2 ) 52
@Fx
3 Q1 Q2
2yx
=
@y
2 4⇡✏✏o (x2 + y 2 + z 2 ) 52
@Fy
3 Q1 Q2
2xy
=
2
@x
2 4⇡✏✏o (x + y 2 + z 2 ) 52
• Coulomb-Kraft vermittelt alle Arten chemischer Bindung
• Um festen Bindungsabstand zu realisieren, abstoßende und anziehende
Kraft (Potential) nötig
9
3
Abstoßendes Potential
• Born-Mayer-Potential (folgt aus Pauli Prinzip)
•
V (r) = EG e
2rs r
%
• EG ist dabei die Abstoßungsenergie bei r = rs , wobei rs ungefähr dem
Atomradius entspricht
4
Bindungsarten
4.1
Ionische Bindung:
• Abstoßung nach Born-Mayer, Anziehung durch reine Coulomb-Wechselwirkung
4.2
Kovalente Bindung
• Erinnerung:
~ beschrieben, Eigenfunktion
– Elektronen durch Wellenfunktion (r)
nlm
– LCAO-Theorie: Linearkombination der Atomorbitale gibt Wellenfkt. mit erhöhter und erniedrigter Elektronendichte zwischen den
Atomrümpfen
– Wellenfunktionen der Atomorbital müssen überlappen, falleb exponentiell mit dem Radius ab
• Empirisches Potential
V (r) =
1 qe2
e
4⇡✏✏o r
r
⇣
• Fällt steiler ab als Coulomb-Potential (kürzere Reichweite). Ursache:
Verringerung des Überlapps der Wellenfunktionen, die exponentiell abfallen.
10
4.3
4.3.1
Schwache Bindungen
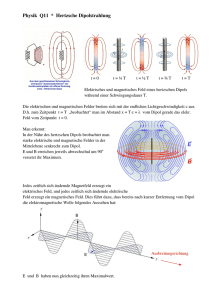
Elektrischer Dipol
• Dipolmoment µ = |q|d
• Elektrisches Feld:
~ r) =
E(~
1
3~
er (~eµ · ~er )
µ
4⇡""0
r3
~eµ
mit den Einheitsvektoren ~er und ~eµ gemäß der Skizze
11
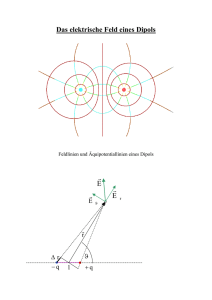
4.3.2
Potentielle Energie einer Punktladung qp im Dipolfeld
VQD (~r) = V q (r) + V+q (r)
"
qp q
qp ( q)
=
+
~
4⇡""o | ~r d2 | 4⇡""o | ~r +
!
qp q
1
1
=
4⇡""0 | ~r d~ | | ~r + d~ |
2
qp q
=
4⇡""0
qp q
=
4⇡""0 r
1
d
r + 2 cos ↵
1
1
d
2r
|
2
1
d
cos ↵
2
r
d~
2
#
!
1
cos ↵
!
1+
d
2r
1
d
cos ↵
2r
cos ↵
mit
(1 + x)n ⇡ 1 + nx
=
=
VQD (~r) =
VQD (~r) =
✓
qp q
d
1+
cos ↵
4⇡""0 r
2r
✓
◆
qp q
d
cos ↵
4⇡""0 r r
qp qd cos ↵
4⇡""0 r2
qp µ~eµ~er
4⇡""0 r2
mit dem Dipolmoment µ = qd
• Die Kraft folgt aus F~ =
~ (~r):
rV
[3 (~eµ~er ) ~er ~eµ ] qp µ
F~ (~r) =
4⇡""0 r3
12
◆
4.3.3
Potential eines Dipols im Dipolfeld
• Gesamtpotential ist Summe der Potentiale der beiden Einzelladungen
des zweiten Dipols
2
3
VDD = V+qp + V
qp
=
qp µ~1~er 6
1
4⇣
⌘
~ 2
4⇡""o
~r d2
1
7
⇣
⌘2 5
~
~r + d2
• Kann analog zu oben behandelt werden, Rechnung liefert:
VDD =
1 µ
~ 1µ
~P
4⇡""o
z
µ1 µP ~eµ1 ~eµP
=
4⇡""o
~ µ1
=µ
~P E
3 (~er · µ
~ 1 ) (~er · µ
~P )
r3
Orientierungsfaktor
}|
{
3 (~er · ~eµ1 ) (~er · ~eµP )
r3
Beispiele!
• Bei freier Rotation muss man den Mittelwert bilden, was zu einer 1/r6
- Abhängigkeit führt
13
4.3.4
Potential Dipol und Influenzierter Dipol
• Jedes Atom ist polarisierbar (Verschiebung der Ladungsdichteverteilung
der Elektronen gegen den Kern)
• influenzierter (induzierter) Dipol im elektrischen Feld:
~
µ
~ = ↵"o E
• Damit kann man die Wechselwirkungsenergie (Potential) des influenzierten Dipols im Dipolfeld bestimmen
• Wir wollen hier die exakte Form gar nicht betrachten, nur die Abhängigkeit vom Abstand r
V DDi =
4.3.5
~ =
µ·E
~E
~ =
↵""o E
↵""o |E|2 / 1/r6
Sich gegenseitig influenzierende Dipole
• Quantenmechanisch kann man zeigen, dass sich zwei Atome gegenseitig
influenzieren können !Von-der-Waals-Anziehung
• Das Lennart-Jones Potential besteht aus einem Van-der-Waals-Anziehungsterm
und einem Abstoßungsterm
• Abstoßung ist Quadrat des Anziehungsterms (weil es sich so schön einfach rechnet)
VLJ (r) = V0
4.3.6
✓⇣
ro ⌘12
r
2
⇣ r ⌘6 ◆
o
r
Wasserstoffbrückenbindung
• allgemein akzeptierter analytischer Ausdruck noch nicht gefunden
• trotz gerichteteten Charakters oft als Zentralpotential genähert der
Form
VHH = Ar 12 Br 10
14