AGEO3.4

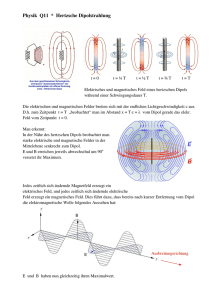
Geophysik
3. Prozesse im Erdinneren
Wir beobachten Prozesse im Erdinneren, die auf sehr verschiedenen Zeitskalen ablaufen.
Während die Mantelkonvektion so langsam ist, dass sie nur indirekt beobachtet werden kann,
lässt sich die Konvektion im äußeren Kern der Erde anhand der Säkularvariation des Erdmagnetfeldes direkt beobachten, weil auf Zeitskalen von wenigen Jahren bereits merkliche Änderungen passieren.
3.4. Das Erdmagnetfeld
Die Form des Erdmagnetfeldes ist zwar die eines Dipolfeldes, aber das Feld wird nicht durch
einen Dipol erzeugt, sondern durch einen hydromagnetischen Dynamo. Die Formen des Strömungsfeldes und des Magnetfeldes sind sehr kompliziert. Wir zeigen zunächst, warum das
Magnetfeld von außen trotzdem etwa wie das Feld eines Dipols aussieht. Die genaue Wirkungsweise des hydromagnetischen Dynamos wird in einer eigenen Vorlesung beschrieben
(was ist denn daran so kompliziert? Beim Scheibendynamo wird durch die Bewegung eines
Leiters im Magnetfeld ein elektrisches Feld induziert, dessen Strom durch eine geeignete Spule zur Verstärkung dieses Magnetfeldes verwendet wird. Wie soll man im flüssigen äußeren
Erdkern ein Analogon zu dieser Spule schaffen? Es kommt darauf an, die Feldlinien zu verbiegen, damit der Strom in die gewünschte Richtung fließt).
Ein qualitativer Hinweis auf die Existenz des ‚Dynamo in der Flüssigkeit’ ist die Säkularvariation, das ist eine langsame zeitliche Änderung der Form und der Amplitude des Magnetfeldes. Sie ist überhaupt nur messbar, weil das Magnetfeld nicht genau die Form eines Dipolfeld
mit einem parallel zur Rotationsachse angeordneten Dipol hat (der würde nämlich, selbst
wenn er verdreht wird, immer dasselbe Feld erzeugen). Auf einer Zeitskala von einigen tausend Jahren ‚eiert’ der Dipol um die Rotationsachse.
Wenn man aber über ca 10 5 Jahre mittelt, ergibt sich doch wieder ein parallel zur Rotationsachse ausgerichteter Dipol. Auf dieser (nur für die jüngste geologische Vergangenheit beweisbaren) Hypothese beruht die Methode des Paläomagnetismus, mit dem sich großräumige
Bewegungen von Lithosphärenplatten rekonstruieren lassen, wenn diese irgendwo eine geologische Struktur mit remanenter Magnetisierung haben (z.B. einen Vulkan, dessen basaltische Lava Magnetit enthält).
1
3.4.1 Ist das Magnetfeld der Erde ein Dipolfeld?
(Sieht es aus wie das Feld eines Stabmagneten?)
Außerhalb der Quellen kann man ein magnetisches Dipolfeld als Gradient eines skalaren PoM cos 
tentials    °
(M.1)
4 r 2
auffassen. Komponenten in Kugelkoordinaten r,  ,  (M: Dipolmoment Am 2 ).

d
2 M cos  
 °
dr
4 r 3 

d
M sin  
B  
 °
rd
4 r 3 
B  0 , Rotationssymmetrie

Br  
Graphik
(M.2)
Form entspricht etwa der Form des Erdmagnetfeldes. Aber: ein Stabmagnet würde wegen
T > TCurie im tiefen Erdinneren seinen Ferromagnetismus verlieren!
Genaue Form des Erdmagnetfeldes (Gauss 1838):
Ersetze das Potential (M.1) durch
 r
  r  
n 1  r




  n 1
 g
n
m0
m
n

cos m  hnm sin m nm cos  
m
Nb n : zugeordnete Kugelfunktion
(M.3)
 nm : Kugelflächenfunktion
Nb Zweidimensionale Entwicklung auf der Kugeloberfläche

9
 9 Vs 

Nb Einheiten so gewählt, dass g, h in nT 1nT  10 T  10
m2 

In g1° (n=1, m=0, 1° cos    cos  ) erkennen wir den Dipolterm (M.1) mit
cos 
1°  r3 g1° 2
g1°  30000nT ( Br (  0) an der Oberfläche r  rE )
r
Nb Fehlen von g °°  Es gibt keine magnetische Monopole.
m
m
Die Bestimmung der Koeffizienten g n , hn ist im Skript ‚Kugelfunktionen’ erläutert.
Für die höheren Terme ergibt sich ein kontinuierlicher Abfall der „spektralen Energiedichte“
2
n
W  (n  1)  g nm  hnm um etwa den Faktor 3 pro „Grad“
2
2
m 0
Dieser Abfall rechtfertigt es scheinbar, das Erdmagnetfeld als ‚Feld eines Dipols’ zu bezeichnen. Dies ändert sich, wenn wir das Feld an der Kern-Mantel-Grenze (core mantle boundary
CMB) betrachten: Der unterschiedlich starke Abfall von Dipol-, Quadrupol- usw. Term wird
dafür durch den Korrekturfaktor
WCMB
 r 
  E 
 rKern 
2( n2)
W
korrigiert. (für den Dipol, n + 2 = 3, korrigiert dies für die r 3 Abhängigkeit der Kraftflussdichte, für den Quadrupol die r 4 Abhängigkeit etc...) Danach haben die Terme für alle n etwa
die gleiche Energie, d.h. die Vormacht des Dipol ist weitgehend verschwunden. In der Gleichverteilung sehen wir einen ersten Hinweis auf eine Koexistenz von gross- und kleinräumigen
Wirbeln. Anders ausgedrückt: Dass wir etwa ein Dipolfeld 'sehen', liegt nur daran, dass die
Instrumente auf der Erdoberfläche bzw. im nahen Weltraum sind.
3.4.2 Die Säkularvariation
a)
b)
c)
Abnahme des Dipolmomentes, zZ 8%/100y
Westdrift des Nichtdipolfeldes, z.Z. 20°-40°/100y
Nicht-driftende Säkularvariation
zu a) Wenn dieser Prozess linear über große Zeiten weiterlaufen würde, wäre nach 1200
Jahren g10  0 . Aus dem Paläomagnetismus sind Umpolungen mit zeitlichen Abständ 104 ... 107 y bekannt. (Vorgriff: Wir sehen später, dass die zeitliche Umpolungsfolge fraktal ist, es gibt also keinen typischen Zeitabstand zwischen 2 Umpolungen, sondern es tritt ein Nebeneinander von allen Intervalllängen auf)
zu b) In ca 1000 Jahren dreht sich dieses Nichtdipolfeld also einmal um sich selbst
3
3.4.3
Der hydromagnetische Dynamo
Aus den Maxwell’schen Gleichungen sowie dem modifizierten Ohm’schen Gesetz mit Lorentz-Term
j =       
(M.4)

und der Kontinuitätsgleichung       0 für inkompressible Flüssigkeit mit  = konst.,
  0
(M.5)
kann man die sog. Dynamogleichung ableiten:


1
 2        
 °
(M.6)

die den zeitlichen Verlauf B bei vorgegebenem Geschwindigkeitsfeld  beschreibt. 1. Term:
Diffusion, Zerfall. 2. Term: Erzeugung. Das Verhältnis
  v  B 
1
2 
 °

 °l°
 Rmag
1
 °
(M.7)
heißt magnetische Reynoldszahl und ergibt sich für den äußeren Kern (   2.5  10 5 S / m ,
ℓ°  3500 km,  °  20 km/a) zu Rmag  500
Da M.6 nur den kinematischen Dynamo ( vorgegeben) beschreibt, brauchen wir eine zweite
Gleichung, die die Rückwirkung von  auf das Geschwindigkeitsfeld  beschreibt, die
Navier-Stokes-Gleichung
0 Experimentalphysik
N
 m 3 

   (  )  p   2 
Reynoldszahl
Nb
(M.8)
  2    J   
Coriolis Lorentz
zusätzliche Kräfte
im Erdkern
 ° ℓ°
Inertial


viskose Kräfte
Für Erdkern modifizierte Navier-Stokes Gleichung ist nicht
linear in B  chaotischer Verlauf möglich
M.6 und M.8: 2 vektorielle DGLn für 2 vektorielle unbekannte Felder B, v
4
Busses Weg:
Erst (M.8) ohne Lorentzterm lösen  v . Dieses v in (M.6) einsetzen  B  Jetzt
(M.8) mit Lorentzterm. Auf diesem Weg erhielt Busse (1975)
sein Modell der Rotationswalzen.
Wird wegen des enormen Rechenaufwandes hier nicht nachvollzogen.
Auftreten der Corioliskraft in M.8 erklärt qualitativ, dass, wenn ein Dipolterm auftritt,
der ' Dipol ' etwa Rotationsachse.
Der 2. Term auf der rechten Seite von (M.6) ist dieser Erzeugungsterm. Allgemein gilt für die
Rotation eines Vektorprodukts
  v  B   v   B   B   v   B    v  v    B
(M.9)
und wegen  B  0 und (M.5)  v  0
  v  B   B    v  v    B

    
 d vx

 Bx
d
x

 dvy

 Bx
dx

 B d vz 
 x dx



Der Term Bx

  
d vx
By
dy
dvy
By
dy
d vz
By
dy
  
d vx
 Bz
dz
dvy
 Bz
dz
d vz
 Bz
dz
(M.10)













„Ableitung von v nach B
d vy
in der y-Komponente dieses Vektors bedeutet: Wenn zunächst nur
dx
B  Bx , 0, 0  und die Geschwindigkeitskomponente vy einen Gradienten in x-Richtung hat,
kann eine zusätzliche Ḃ y -Komponente erzeugt werden.


Warum ist es so wichtig, das Magnetfeld zu „verbiegen“ Bx  B˙ y ? Diese Frage führt auf
die Antidynamo-Theoreme, die Dynamos mit einfacher Geometrie des Magnetfeldes oder des
Geschwindigkeitsfeldes ausschließen.
5
Zusammenfassung: Hydromagnetischer Dynamo: Schnelle Konvektion einer elektrisch leitfähigen Flüssigkeit (äußerer Erdkern: Fe und eine weitere leichtere
Komponente(?))
3.4.4. Paläomagnetismus
Corioliskraft in M.8: Hypothese: Der ' Dipol ' war immer (zu allen geologischen Zeiten) zur
Rotationsachse der Erde. Weil es nach (M.2) eine eineindeutige
Beziehung zwischen der Inklination I und der Kobreite  gibt (
tan I  Br
 2 cot  ), müßte eine ' Kontinentalverschiebung '
B
in NS Richtung messbar sein:
Szenario :
Vulkanausbruch vor 300 Mio Jahren (  radioakt. Altersbestimmung, s. Kap. 2.4) basaltische
Lava enthält ~5% Magnetit, der ferrimagnetisch ist. Unmittelbar nach dem Ausbruch:
T  TCurie  600 keine remanente Magnetisierung
Abkühlung: T  TCurie , Lava  Basalt
erwirbt remanente Magnetisierung J parallel zum Erdmagnetfeld H
Nach der 'Kontinentalverschiebung' hat das Erdmagnetfeld am neuen Ort des Vulkans eine
andere Inklination, und deshalb ist J nicht mehr H
Inklination der Basaltprobe ǂ Inklination Erdmagnetfeld
Diese Methode ergab die ersten physikalischen Beweise für großräumige Bewegungen von
Lithosphärenplatten. Dieser Gedankengang wird in Kap. 4.3 weitergeführt!
6