Zusammenfassung

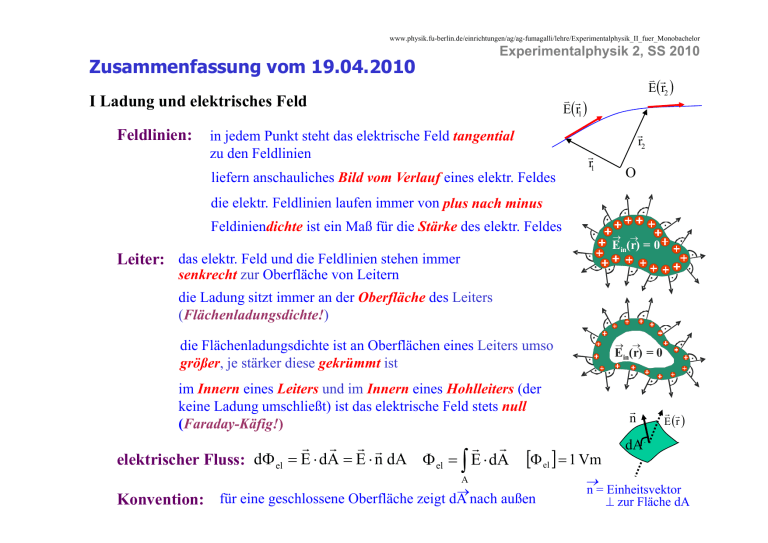
www.physik.fu-berlin.de/einrichtungen/ag/ag-fumagalli/lehre/Experimentalphysik_II_fuer_Monobachelor
Experimentalphysik 2, SS 2010
Zusammenfassung vom 19.04.2010
v r
E( r1 )
I Ladung und elektrisches Feld
Feldlinien:
v r
E( r2 )
in jedem Punkt steht das elektrische Feld tangential
d Feldlinien
ldli i
zu den
liefern anschauliches Bild vom Verlauf eines elektr. Feldes
r
r2
r
r1
O
die elektr. Feldlinien laufen immer von pplus nach minus
Feldiniendichte ist ein Maß für die Stärke des elektr. Feldes
→
→
Ein(r) = 0
Leiter: das elektr. Feld und die Feldlinien stehen immer
senkrecht
k ht zur Oberfläche
Ob flä h von Leitern
L it
die Ladung sitzt immer an der Oberfläche des Leiters
(Flächenladungsdichte!)
→
die Flächenladungsdichte ist an Oberflächen eines Leiters umso
größer, je stärker diese gekrümmt ist
im Innern eines Leiters und im Innern eines Hohlleiters ((der
keine Ladung umschließt) ist das elektrische Feld stets null
(Faraday-Käfig!)
r r r r
r r
dΦ el = E ⋅ dA = E ⋅ n dA Φ el = ∫ E ⋅ dA
elektrischer
l kt i h Fluss:
Fl
r
n
[Φ el ] = 1 Vm
V
A
→
Konvention: für eine geschlossene Oberfläche zeigt dA nach außen
→
Ein(r) = 0
→
r r
E (r )
dA
n = Einheitsvektor
⊥ zur Fläche dA
Zusammenfassung vom 19.04.2010
www.physik.fu-berlin.de/einrichtungen/ag/ag-fumagalli/lehre/Experimentalphysik_II_fuer_Monobachelor
r r r Q innen
Gauß‘sches Gesetz: Φ el = ∫ E( r ) ⋅ dA =
ε0
AV
Integral-Form
r r r ρ(rr )
r r
∇ ⋅ E(r ) =
= div E( r )
ε0
Experimentalphysik 2, SS 2010
AV = geschlossene
hl
Ob
Oberfläche
flä h um V
Volumen
l
V
Qinnen = im Volumen V eingeschlossene Ladung
r
r dq
d (r )
= Volumenladungsdichte
ρ(r ) =
dV
r
∇ = (∂ ∂x , ∂ ∂y , ∂ ∂z ) = Nabla-Operator
differentielle Form („Divergenz von E“)
Verständnisfragen: Feldlinien dienen der Veranschaulichung des Verlaufs des elektrischen
Feldes. Welche
Information geht dabei im Vergleich zur mathematischen
¤¤
Darstellung E( r ) verloren, welche bleibt erhalten und welche kann
besonders gut dargestellt werden?
In einer kugelförmigen Box befindet sich eine unbekannte Ladungsmenge. Nun wird der elektrische Fluss gemessen, einmal über eine
kugelförmige und einmal über eine würfelförmige Oberfläche, die beide
die Box enthalten
enthalten. Sind die beiden Flussintegrale gleich groß? Wie sieht
es aus, wenn nur jeweils exakt über die halbe Oberfläche integriert wird?
In einer Box befindet sich ein elektrischer Dipol, eine weitere, äußerlich
id i h Box
identische
B ist
i jedoch
j d h leer.
l
Kann
K
man, ohne
h die
di beiden
b id Boxen
B
zu
öffnen, herausfinden, welche leer ist? Spielt es hierbei eine Rolle, ob die
Boxen aus Metall oder aus einem nichtleitenden Material sind?