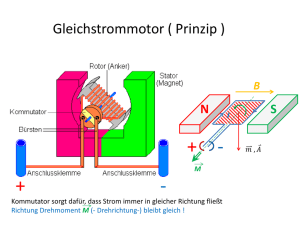
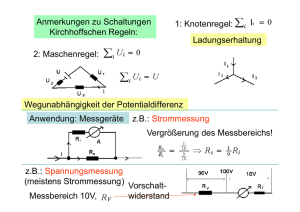
Magnetismus

Anorganische Chemie II
Magnetismus
Skript zur Vorlesung Magnetismus
Mai 2007
Dieses Skript soll einen kurzen Überblick über Magnetismus und magnetische Phänome geben. Es ist als Ergänzung zum Skript zur Anorganischen Chemie II von Markus
Schwind gedacht. Es besteht keine Garantie zur Vollständigkeit. Gefundene Tipp und
Formatierungsfehler könne natürlich gerne mitgeteilt werden.
Mainz, den 24. Mai 2007
Timo Schüler
[email protected]
c
Timo
Schüler
2
INHALTSVERZEICHNIS
1 Grundlegende Theorie
4
2 Dia- und Paramagnetismus
2.1 Diamagnetismus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.2 Pamagnetismus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5
5
5
3 Kollektiver Magnetismus
3.1 Ferromagnetismus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.2 Antiferromagnetismus . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.3 Ferrimagnetismus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
7
9
9
4 Ideale Diamagneten: Supraleitung
11
3
KAPITEL 1
Grundlegende Theorie
Die magnetischen Eigenschaften eines Atoms sind gegeben durch quantenmechanische Eigenheiten. Ein sich um einen atomaren Kern kreisendes Elektron induziert
ein Magnetfeld. Durch den Bahndrehimpuls besitzt ein Elektron ein magnetisches
Moment. Nur s-Elektronen besitzen kein magnetisches Moment da bei ihnen l=0 gilt.
Ein Magnetfeld wird allgemein durch die magnetische Induktion oder magnetische
~ beschrieben. Anschaulich beschreibt diese Flussdichte, die Dichte der
Flussdichte B
Feldlinien an einem bestimmten Punkt. Sie ist gegeben durch
~ = µ0 H
~
B
(1.1)
mit µ0 der magnetischen Feldkonstante im Vakuum. Bringt man nun einen Körper in
ein homogenes magnetisches Feld ein, existiert im Körper ein zu Baussen unterschiedliches Binnen . Hierbei zeigen sich zwei Grenzfälle: Entweder werden die magnetischen
Feldlinien im Körper verdichtet, der Stoff wird in das Magnetfeld hineingezogen,
oder die Feldlinien werden aus dem Körper heraus gedrängt, der Stoff wird von
einem Magnetfeld abgestoßen. Der erste Fall wird als Paramagnetismus bezeichnet,
letzterer als Diamagnetismus. Quantitativ lassen sich diese beiden Phänomene mit
Hilfe der magnetischen Suszeptibilität beschreiben:
B=χ·
H
µB
(1.2)
mit µB dem Bohr’schen Magneton. Trägt man die Magnetisierung gegen das angelegte Feld
auf, erhält man χ gerade als Steigung einer Geraden. Mit Hilfe der magnetischen Suszeptibilität lassen sich Stoffe in verschiedene Gruppen unterteilen. Für diamagnetische
Stoffe ist χ < 0, für paramagnetische Stoffe gilt χ > 0, für ferromagnetische Stoffe
χ >> 0. Diese Phänomene sollen im Anschluss besprochen werden. [1]
4
KAPITEL 2
Dia- und Paramagnetismus
2.1 Diamagnetismus
Zunächst handelt es sich beim Diamagnetismus, ebenso wie beim Paramagnetismus,
um die magnetischen Eigenschaften eines einzelnen Atoms; es handelt sich umgangssprachlich um “verdünnten“ Magnetismus. Im Gegensatz dazu steht der “kollektive“
Magnetismus, wobei man sich die magnetischen Eigenschaften nicht nur eines Atoms,
sondern eines ganzen Atom-Verbands anschaut. Auf diesen wird in Abschnitt 3 eingegangen. Zum Verständnis des Diamagnetismus genügt die klassische Vorstellung
von den Bahnen der Atomelektronen, die mit der umlaufenden Elektronenladung
einer Stromschleife, also einem magnetischen Bahnmoment entsprechen, und mit der
umlaufenden Elektronenmasse einen Bahndrehimpuls definieren. Wird ein äußeres
Magnetfeld eingeschaltet, dann übt das Feld H auf das magnetische Moment µ ein
Drehmoment aus. Da das magnetische Moment aber mit dem Bahndrehimpuls l gekoppelt ist, reagiert die Elektronenbahn auf das Drehmoment wie ein Kreisel und
beginnt um die Feldrichtung zu präzedieren. Die Präzessionsbewegung der Elektronenbahn entspricht einem induzierten Strom, der -in Übereinstimmung mit dem
Lenz’schen Gesetz- ein Magnetfeld erzeugt, das dem äußeren Magnetfeld entgegengesetzt ist. Zum Diamagnetismus tragen hauptsächlich die äußeren Elektronen bei.
Die Präzessionsbewegung ist dabei Temperatur- und Feldunabhängig. Trägt man
hier die Magnetisierung gegen die Temperatur auf, erhält man also eine Parallele
zur x-Achse. Atome von diamagnetischen Stoffen haben abgeschlossene Schalen, alle
magnetischen Bahn- und Spinmomente kompensieren sich gegenseitig.
2.2 Pamagnetismus
Der Paramagnetismus entsteht durch nicht kompensierte Bahn- und Spinmomente,
die beide mit dem Drehimpuls gekoppelt sind. Allerdings sieht man beim Parama-
5
2.2. PAMAGNETISMUS
KAPITEL 2. DIA- UND PARAMAGNETISMUS
gnetismus eine Temperatur- und Feldabhängigkeit. Dies lässt sich wie folgt erklären:
Die magnetischen Momente können sich nicht einfach parallel zum äußeren Feld
ausrichten, weil damit Drehimpulse verbunden sind, für die nach der Quantenmechanik nur diskrete Orientierungen, genauer gesagt magnetische Zustände, im Feld
erlaubt sind. Die energetischen Abstände zwischen diesen Zuständen wachsen mit
zunehmendem H. Nach Boltzmann werden diese Zustände bei geringer Temperatur
ungleich besetzt. Energetisch tiefliegende Zustände, mit paralleler Ausrichtung der
magnetischen Momente, werden dabei stärker besetzt als die energetisch höher liegenden Zustände, mit antiparalleler Ausrichtung der magnetischen Momente. Mit
zunehmender Temperatur werden die letztgenannten Zustände immer häufiger besetzt und somit sinkt das paramagnetische Moment.
Quantitativ lässt sich die Temperaturabhängigkeit des Paramagnetismus durch das
Curie-Weiss-Gesetz beschreiben:
χ=
C
T − TC
(2.1)
mit C der Curie-Konstante und TC der Curie-Temperatur. [2, 3] Die Temperaturabhängigkeit ist in Abbildung 2.1 dargestellt.
Abbildung 2.1: Abhängigkeit der Magnetisierung von der Temperatur beim Paramagnetismus [1]
6
KAPITEL 3
Kollektiver Magnetismus
Um den uns bekannten Magnetismus von z.B. Haushaltsmagneten zu verstehen,
müssen wir uns dem sogenannten kollektiven Magnetismus widmen. Hier koppeln
die oben besprochenen magnetischen Eigenschaften der Atome untereinander und
können so nach außen hin ein größeres magnetisches Moment zeigen.
3.1 Ferromagnetismus
Abbildung 3.1: Zusammenhang Abstand und Austauschwechselwirkung
Ferromagnetismus ist ein typisches kollektives, magnetisches Phänomen, welches
nur bei Festkörpern auftritt. Hierbei betrachtet man nicht die Eigenschaften eines einzelnen Atoms sondern schaut sich den gesamten Festkörper an. Die elektronischen
Niveaus werden hier insgesamt nach den Hund’schen Regeln besetzt. Es entsteht
ein Leitungs- und ein Valenzband. Bei der Auffüllung des Valenzbandes konkurrieren nun zwei entgegengesetzte Effekte. Sollen die Spins parallel ausgerichtet sein,
so müssen Elektronen in unbesetzte Niveaus oberhalb der Fermi-Kante angehoben
werden, dadurch verringert sich jedoch die elektrostatische Abstoßung zwischen den
Elektronen. Bei einer hohen Zustandsdichte an der Fermi-Kante liegen die Energieniveaus sehr dicht, so dass die Elektronen nur einen kleinen Energiebetrag benötigen,
um ihre Spins parallel stellen zu können. Die Zustandsdichte hängt nun unter anderem von den atomaren Abständen ab. Ist der Atomabstand gering, besteht eine
7
3.1. FERROMAGNETISMUS
KAPITEL 3. KOLLEKTIVER MAGNETISMUS
starke Niveauaufspaltung und ein hoher Energieaufwand ist zur Neuverteilung der
Elektronen nötig (Abbildung 3.1 , links); es resultiert Antiferromagnetismus (s.u.). Ist
dagegen der Atomabstand groß, kann keine Kopplung von magnetischen Momenten
stattfinden(Abbildung 3.1 , rechts); es resultiert normaler Paramagnetismus. Ab einem
bestimmten Abstand besteht eine geringe Niveausaufspaltung und somit ist wenig
Energie aufwendig um Elektronen neu zu verteilen(Abbildung 3.1 , Mitte); es resultiert
Ferromagnetismus. Der genaue Zusammenhang zwischen Abstand und Austauschenergie ist in gezeigt Abbildung 3.2 [4] . Wie beim Paramagnetismus ist auch beim
Abbildung 3.2: Bethe-Slater-Kurve
Ferromagnetismus eine Temperaturabhängigkeit zu beobachten (s. Abbildung 3.3),
da auch hier die thermische Bewegung der Elektronen der Spinausrichtung entgegen
wirkt. Ab einer bestimmten Temperatur, der Curie-Temperatur TC , verschwindet die
spontane Magnetisierung völlig und es ist nur noch normaler Paramagnetismus zu
beobachten. Ferromagnetismus tritt nur bei wenigen Stoffen auf. Er ist nur bei den
3d-Übergangsmetallen Fe (TC = 1043 K), Ni (TC = 1404 K), Co (TC = 631 K) und bei
den Lanthaniden Gd (TC = 298 K), Dy (TC = 85 K) und Ho (TC = 20 K) bekannt. [2]
Abbildung 3.3: Abhängigkeit der Magnetisierung von der Temperatur beim Ferromagnetismus [1]
8
3.2. ANTIFERROMAGNETISMUS
KAPITEL 3. KOLLEKTIVER MAGNETISMUS
3.2 Antiferromagnetismus
Abbildung 3.4: Abhängigkeit der Magnetisierung von der Temperatur beim Antiferromagnetismus [1]
Von Antiferromagnetismus ist die Rede, wenn sich benachbarte Spinmomente über
den gesamten Kristall kompensieren. Dabei wechseln sich spin-up und spin-down
Atome ab. Makroskopisch gesehen ist somit keine Magnetisierung feststellbar. Allerdings ist unterhalb einer bestimmten Sprungtemperatur, der Néel-Temperatur TN ,
die magnetische Suszeptibilität χ temperaturunabhängig. Oberhalb dieser Temperatur zeigen antiferromagnetische Stoffe wieder paramagnetisches Verhalten (s. Abbildung 3.4). Antiferromagnetismus tritt z.B. bei Mn (TN = 100K), Cr (TN = 308 K)
und MnO (TN =110 K) auf. Erklären lässt sich die antiferromagnetische Kopplung von
Verbindungen durch zwei ineinander verschachtelte Untergitter mit entgegengesetzt
gleicher Magnetisierung. Beim Ferromagnetismus sind die Spinmomente alle gleich
ausgerichtet; bei Antiferromagnetismus sind sie nur innerhalb der Untergitter gleichgerichtet, während die Untergitter in entgegengesetzter Richtung magnetisiert sind.
Auf den Gitterplätzen der Antiferromagnetika befinden sich magnetische Momente von gleichem Betrag, so dass wie schon oben angedeutet, nach außen hin keine
Magnetisierung in Erscheinung tritt. Die durch einen Liganden vermittelte antiferromagnetische Kopplung bezeichnet man als Superaustausch (Abbildung 3.5 ).
3.3 Ferrimagnetismus
Ferrimagnetismus tritt nur bei einer bestimmten Stoffklasse, den Ferriten auf. Diese zeichnen sich durch zwei verschieden Untergitter, mit einer unterschiedlichen
Gitterplatz-Anzahl, aus. Auch hier sind, wie beim Antiferromagnetismus, die Momente in den beiden Untergittern für sich wiederum parallel und die beiden Untergitter antiparallel ausgerichtet. Allerdings sind auf den Plätzen des einen Untergitters
magnetische Momente mit höherem Betrag lokalisiert als auf den Plätzen des anderen Untergitters. Somit kompensieren sich die magnetischen Momente nicht komplett
und der Stoff zeigt nach außen hin eine spontane Magnetisierung. Nach außen hin
verhält sich ein ferrimagnetischer Stoff also ähnlich zu einem ferromagnetischen Stoff.
9
3.3. FERRIMAGNETISMUS
KAPITEL 3. KOLLEKTIVER MAGNETISMUS
Abbildung 3.5: Superaustausch-Wechselwirkung
Allerdings zeigt der Stoff ab einer bestimmten Temperatur, der sog. Kompensationstemperatur, nach aussen hin ein antiferromagnetisches Verhalten. Bei dieser Temperatur
gleichen sich die magn. Momente der beiden Untergitter gerade aus.
Abbildung 3.6: Abhängigkeit der Magnetisierung von der Temperatur beim Ferrimagnetismus [4]
10
KAPITEL 4
Ideale Diamagneten: Supraleitung
Abbildung 4.1: Meissner-Ochsenfeld-Effekt; oben: normaler Leiter; unten: Supraleiter
Quecksilber zeigt unterhalb von 4.15 K keinen elektrischen Widerstand. Dieser Effekt wird als Supraleitung bezeichnet. Auch viele andere Metalle des Periodensystems
zeigen diesen Effekt, vorwiegend Metalle, die weder ferro- noch antiferromagnetisch
koppeln. Allgemein gilt, dass gute Leiter (Ag, Cu) schlechte Supraleiter und schlechte
Leiter (Pb, Nb) gute Supraleiter sind. Die Temperatur, unterhalb derer der elektrische
Widerstand verschwindet, heißt Sprungtemperatur TC (critical temperature). Oberhalb
eines kritischen Magnetfelds BC bricht die Supraleitung zusammen. Die kritische Feldstärke ist abhängig von Material und Temperatur. Charakteristisch für Supraleiter ist
nicht nur das Verschwinden des elektrischen Widerstands, sondern auch, dass in seinem Inneren die magnetische Feldstärke B gleich null ist. Der Supraleiter ist unterhalb
der Sprungtemperatur und unterhalb der kritischen Feldstärke ideal diamagnetisch.
Es gilt
χ = −1
(4.1)
Wird eine supraleitende Probe in ein Magnetfeld B < BC eingebracht, kann der Magnetfluss nicht eindringen, die Feldlinien laufen um die Probe herum (Abbildung 4.1
11
KAPITEL 4. IDEALE DIAMAGNETEN: SUPRALEITUNG
). Wird die Probe über die Sprungtemperatur erwärmt, dringt der Fluss wie in jedes
normal leitende Material ein. Beim erneuten Abkühlen unter die Sprungtemperatur
wird der Fluss aus der Probe heraus getrieben. Dieser Effekt ist allgemeinhin bekannt
als Meissner-Ochsenfeld-Effekt. [1]
Abbildung 4.2: Meissner-Ochsenfeld-Effekt: Magnet über Supraleiter [5]
12
LITERATURVERZEICHNIS
[1] B. Schaefer. Lehrbuch der Experimentalphysik, Band 2, Elektromagnetismus. Walter de
Gruyter, Berlin, 2006.
[2] B. Balke. Heusler-Verbindungen mit 28,5 Valenzelektronen. Diplomarbeit, Universität
Mainz, Mainz, 2004.
[3] E. Riedel. Anorganische Chemie. Walter de Gruyter, Berlin, 2004.
[4] B. Schaefer. Lehrbuch der Experimentalphysik, Band 6, Festkörper. Walter de Gruyter,
Berlin, 2005.
[5] P. A. Tipler. Physik. Spektrum Akademischer Verlag, Berlin, 2000.
13