2 Finite Differenzen Methode (FDM)

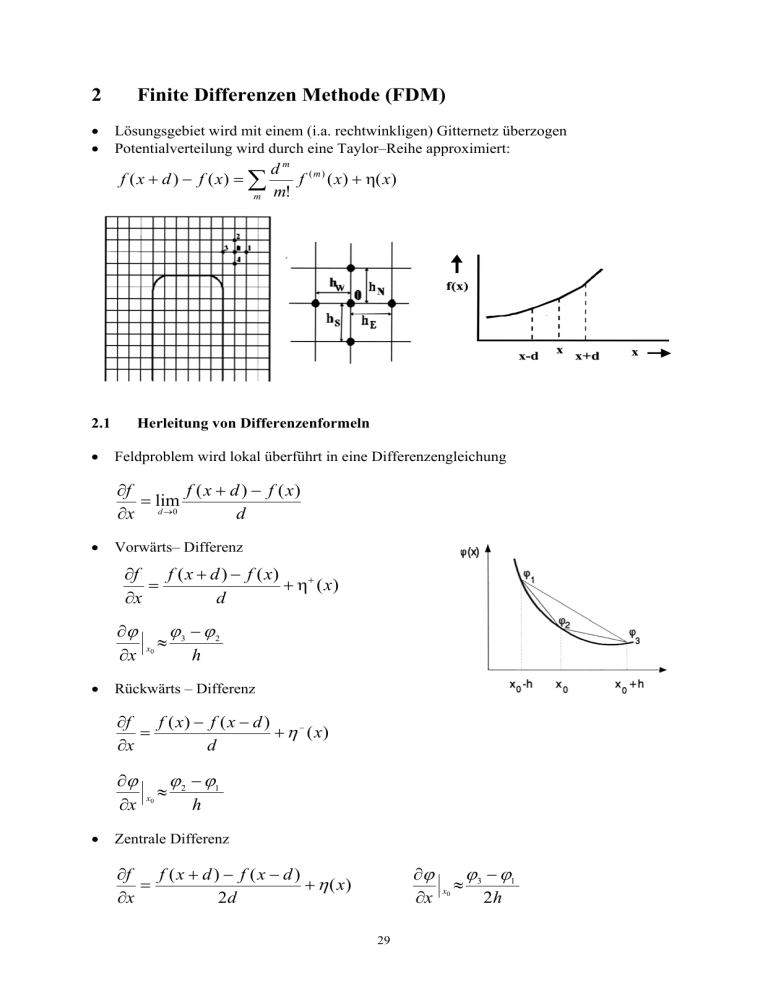
2


Finite Differenzen Methode (FDM)
Lösungsgebiet wird mit einem (i.a. rechtwinkligen) Gitternetz überzogen
Potentialverteilung wird durch eine Taylor–Reihe approximiert:
d m (m)
f ( x  d )  f ( x)  
f ( x)  ( x)
m m!
2.1

Herleitung von Differenzenformeln
Feldproblem wird lokal überführt in eine Differenzengleichung
f
f ( x  d )  f ( x)
 lim
d 0
d
x

Vorwärts– Differenz
f ( x  d )  f ( x)
f
  ( x )

d
x

x

x0

3  2
h
Rückwärts – Differenz
f
f ( x)  f ( x  d )

   ( x)
x
d

x

x0

 2  1
h
Zentrale Differenz

x
f (x  d )  f (x  d )
f

  ( x)
x
2d
29
x0

 3  1
2h
Genauigkeitsvergleich
Taylorreihenentwicklung liefert
1
 1

2
6
 1 2  1 3 
  x  h x  h  x  h  x  ...
2
6

 ( x  h) :  xh   x  h x  h 2 x  h3 x  ...
 ( x  h) :  x h
1. Ableitung ergibt sich mittels Vorwärtsdifferenz

x 
 xh   x
h
1
  x

 1
 O ( h)
 h x  h3 x  ...  xh
2
6
h
und mittels zentraler Differenz

x 
 xh   xh
2h
   x h
1

 h 2 x  ...  x h
 O(h 2 )
6
2h
Für die 1. Ableitung an den Stellen x  h und x  h folgt
2
2


h
x
2

 x h   x

h

h
x
2

 x   xh
h
und damit für die 2. Ableitung an der Stelle x

x 

x
h
2

h
x
h
2

 xh  2   xh
h2
2.1.1 Taylorreihenansatz
Fünf – Punkte – Differenzenstern
Poisson – Gleichung:
2D, kartesisch:
1. Schritt:
  


 2  2
( x, y )
 2   f ( x, y )  
2
x
y


Diskretisierung
30
(1)
Differenzenstern
2. Schritt: Taylorentwicklung für das Potential an der Stelle P0(x0,y0)
 
1 
k
 ( x0 , y0 )
y 
1!  x
 ( x0  h, y0  k )   ( x0 , y0 )   h
2
1 
 
 h
k
  ( x0 , y0 )
2! x
y 
3
1 
 
 h
k
  ( x0 , y0 )  ...
3! x
y 
n
 
1 
k
 h
  ( x0 , y0 )  Rn
n! x
y 
3. Schritt:
Anwendung der Taylorentwicklung auf den Differenzenstern
h12
h13
 1   0  h1 x   xx   xxx  ...
2
6
(2)
h22
h23
 2   0  h2 x   xx   xxx  ...
2
6
(3)
h32
h33
 3   0  h3 y   yy   yyy  ...
2
6
(4)
h42
h43
 4   0  h4 y   yy   yyy  ...
2
6
(5)
4. Schritt:
Ermittlung der Differenzenformel
1  1  2 
1  3 4  1
    f ( x0 , y 0 )
   
h1  h2  h1 h2  h3  h4  h3 h4  2
0 
1
1

h1h2 h3 h4
Sonderfall: h1 + h2 + h3 + h4 = h
(6)
(quadratisches Gitter)
h2
1
 0  (1   2   3   4 )  f ( x0 , y 0 )
4
4
(7)
und für die Laplacegleichung
1
4
 0  (1   2   3   4 )
(8)
31
Neun – Punkte - Differenzenstern
Taylorentwicklung bis Term 4.Ordnung
h12
h13
h14
1  0  h1 x   xx   xxx   xxxx  ...
2
6
24
h22
h23
h24
2  0  h2  x   xx   xxx   xxxx  ...
2
6
24
3  0  h3 y 
h32
h3
h4
 yy  3  yyy  3  yyyy  ...
2
6
24
 4  0  h4  y 
h42
h3
h4
 yy  4  yyy  4  yyyy  ...
2
6
24
5  0  h1 x  h3 y 

1 2
h1  xx  2h1h3 xy  h32  yy
2



1 3
h1  xxx  3h12 h3 xxy  3h1 h32  xyy  h33 yyy
6
1 4

h1  xxxx  4h13h3 xxxy  6h12 h32  xxyy  4h1 h33 xyyy  h34  yyyy  ...
24


 6   0  h 2 x  h 4 y 

1 2
h2  xx  2h2 h4 xy  h42 yy 
2
1 3
h2  xxx  3h22 h4 xxy  3h2 h42 xyy  h43 yyy 
6
1
 h24 xxxx  4 h23 h4 xxxy  6 h22 h42 xxyy  4 h2 h43 xyyy  h44 yyyy   ...
24

7  0  h2  x  h3 y  ...
8  0  h1 x  h4  y  ...
Zusammenfassung der Ableitungen entsprechend der Schwarz´schen Regel, angewendet auf
die Laplacegleichung:
 xx   yy :  xxy   yyy ,  xxx   yyx
 xxxx   yyxx ,  xxyy   yyyy
 xxxy   yyxy ,  xxyx   yyyx
32
Daraus folgt ein Gleichungssystem für die acht Unbekannten:
x  ( 0 , x , y , xy , xx , xxx , yyy , xxxx )T
8
8
i 1
i 1
x  D 1     0   d1i1  i   ci  i

Analytisch auflösbare Spezialfälle des 9–Punkte-Differenzensterns:
a)
reguläres Rechteckgitter :
h1= h2= h, h3= h4= k
1
5k 2  h 2 1   2   5h 2  k 2  3   4 
0 
2
2
10(h  k )
1
  5   6   7   8 
20
b)
äquidistantes Gitter:
1
5
h1= h2= h3= h4= k
 0  1   2   3   4  

Diskretisierungsfehler:
5 – Punkte – Stern:
9 – Punkte – Stern:
1
 5   6   7   8 
20
O(h2)
O(h6)
33
Differenzenformeln für Zylindersymmetrie
Rotationssymmetrie:
Poisson – Gleichung:
 2
0
 2
 2 1    2


  f (r , z )
r 2 r r z 2
h12
1  0  h1 z   zz  ...
2
h2
 2  0  h2  z  2  zz  ...
2
h2
3  0  h3 r  3  rr  ...
2
h42
 4  0  h4  r   rr  ...
2
Elimination der 1. Ableitung r und z, Ausdrücken der 2. Ableitung rr und zz durch die
Knotenpotentiale und Auflösung nach 0 liefert die 5 – Punkte – Differenzenformel:
 
0
2r
h h
1
2





  h h
 
1
4 f (r , z )
3  2r  h
4 3
 1  2 
 2r  h
4 h
3 h 
h
2
h  h h 
4
2
3
4
3
 1
2
r

h

h
2r
4
3

hh
h h
1 2
3 4


Für ein reguläres Rechteckgitter (h1= h2= h, h3= h4= k) ergibt sich:
1
1   2   1 2  3   4   1  3   4 
2
2k
4kr
 0  2h
1
1
 2
2
h
k
und für ein quadratisches Gitter (h = k):
1
4
 0  1   2   3   4  
h
 3   4 
8r
Achsnahe Differenzenformeln
o.g. Formeln gelten nicht in der Nähe der Rotationsachse (r  0)!
Punkte 1 bis 3 vorgegeben:
1
6
 0  1   2  4 3 
Punkte 3, 5, 8 vorgegeben:
1
4
 0  2 3   5   8 
34
Differenzenformel für einen unsymmetrischen Stern:
1  1  2  2
    3
h1  h2  h1 h2  h32
0 
1
2
 2
h1h2 h3
Differenzenformel in Polarkoordinaten
 2
0
z 2
Polarkoordinaten:
 2 1   1  2
0


r 2 r r r 2  2
Laplace – Gleichung:
Vereinfachung:
h1= h2= h
h3= h4= k
h2
1   0  h   
 2   0  h  
2
 rr 
   ...
h2
  ...
2
3  0  k 3 r 
4  0  k r 
(   )
(  r )
k2
2
k2
2
 rr  ...
 rr  ...
 3   4  2 0 
k2
  
1   2  2 0 
h2
5 – Punkte – Differenzenstern:
1
r
r




 3   4 








1
2
3
4
2
2
k
2
2
4
h
k
0 
r2 1

k 2 h2
35
r 
 3   4 
2k
Approximation von Rändern und Grenzen
Randnahe Gitterpunkte
Unregelmäßiger 5 – Punkte – Stern
4
0   qi i
i 1
mit:
q1  qa  h2 , q3  qb  h4
q2  qa  h1 , q4  qb  h3
qa 
h3 h4
h1h3  h2 h4 h1h2 
qb 
h1h2
h1h3  h2 h4 h3 h4 
Unregelmäßiger 9 – Punkte – Stern:
8
0   ci i
i 1
Berechnung der Koeffizienten ci erfordert einen erheblichen Aufwand
 numerische Berechnung
36
Besondere Berandungen ( Symmetrien )
Symmetrien = Linien mit verschwindender Normalkomponente der elektrischen Feldstärke
5 – Punkte – Stern:
3  4
1
4
 0  1   2  2 3 
9 – Punkte – Stern:
2 Symmetrielinien:
3   4 ,5  8 ,6   7
0 
1
1  2  23   1 (5  7 )
5
10
0 
2
1  3   1 5
5
5
Kombination von Symmetrielinie und Randkurve
Differenzenformel eines vollständigen, unregelmäßigen 9 – Punkte – Differenzensterns:
c3  c4 , c5  c8 , c6  c7
 0   ci  i  2  ci  i
i 1, 2
i 3, 5 , 7
37
Grenzflächen im Feldgebiet
Laplace – Gleichung:
- quadratisches Gitter
- kartesische Koordinaten
 2  2

0
x 2 y 2
h2
1  0  h x 1   xx 1
2
h2
2  0  h x 2   xx 2
2
h2
3  0  h y   yy
1
1
2
 4   0  h y 
2
h2
 yy
2
2
Einbeziehung der Grenzbedingungen:
Et  Et
1
2
 x 1  x
2
 1 En   2 En   y 1 
1
2
2

1 y
2
Die 2. Ableitungen müssen in beiden Bereichen die Laplace – Gleichungen erfüllen, die
Grenzknotenpotentiale ergeben sich aus der Taylorentwicklung sowohl im Bereich 1 als auch
im Bereich 2. Folglich gilt auch:
1   0  h x 2 
h2
 xx 2
2
Daraus folgt ein System von neun Gleichungen, das nach Auflösung nach dem Potential 0
die Differenzenformel für einen Grenzknoten liefert:

1
2 1 

  3  2  4 
 0  1   2 
4
1   2 
 1 
Diagonalformel:
0 
( 5 ... 8 bekannt)
1



 5   7  2  6   8 

1
2( 1   2 ) 

38
Erfassung der Randbedingungen
5 – Punkte – Stern für die Laplace – Gleichung:
1   2   3   4  4 0  0
a) Dirichlet–Bedingungen:
hier:
 3  g ( s1 )  g 3 ,
1   2   4  4 0   g 3
b) Neumann – Bedingung:
hier:
( s )  g ( s)
s1 = Knoten 3 auf dem Rand S

 p (s )
n s

  1
 p 2
 p0   2   1  2h  p0
x
2h
21   3   4  4 0  2hp0
c) Cauchy – Bedingung:
hier:
 2  1
2h

 ( s)  ( s)  q( s)
n s
  0   0  q0
1  (q0   0 0 )2h   2
h

2 2   3   4  41   0  0  2hq0
2

39
3D – Approximationen
Differenzengleichung:
(äquidistantes Gitter)
1 6
6 i 1
0   i
Beispiel: Poisson–Gleichung für inhomogene, statische Magnetfelder


 2 
S ( )   m ,  m  divM

 = 0 angenommen
Gleichung mit h multipliziert
Finite – Differenzen – Operatoren:
T ( ) 
S ( )

S ( )  0
Es gilt:
S ( )

S ( ) 
 1   2   3   4   5   6  
 2  ex  2  e y  2  ez 


0
0
0
   2   3   4   5   6  
 1
ex 
ey 
ez 
2
2
 2

  ( 1   2 )   ( 3   4 )   ( 5   6 )
mit:

  4
  6
1   2
,  3
,  5
2 0
2 0
2 0
6
T ( )    i  6 0
i 1
(1  )1  (1  )2  (1  )3  (1  )4  (1  )5  (1  )6  60  0
40
3D – Differenzenstern auf einer Grenzfläche
Punkt 0 auf der Grenzfläche 
 ,  0
 singulär
Berücksichtigung der Grenzbedingungen

1 ( 1   0 )   2 ( 0   2 )

neuer Operator:
41
2.1.2 Umlaufintegralmethode (Integralapproximation der Feldgleichung)
Mathematisches Modell
Prinzipiell existieren 4 Typen von mathematischen Modellen für die Feldberechnung:
1. Aufstellung von pDGL´n + RB und/oder AB

FDM
2. Minimierung der Feldenergie  Variationsaufgabe 
FEM
3. Aufstellung von IGL´n für Feldquellen

IGM
Hier: 4. Ableitung von Beziehungen zwischen Integralen der Feldgrößen mittels
Integralsätzen + RB und/oder AB 
UIM
(Gaußscher Satz bzw. Induktionsgesetz in Integralform)

Bezeichnungen:
- Approximation der Feldgleichungen in Integralform
- Methode nach REICHERT
- Umlaufintegralmethode (UIM)
Klassifizierung der Methode:
nach Lösungsansatz:
nach Art der Approximation:
 Integralverfahren
 FDM
 FEM
Darstellung beider Varianten der näherungsweisen Lösung der Integralform
der Feldgleichungen am Beispiel der Magnetfeldberechnung:
Quasistationäres Magnetfeld
rot H  J
B    H  rotA
1

rot rot A   J    E


rot E  
B
t

 A 
rot  E 
0

t 



E
A
 
t

 A
1

rot  rot A    
    J w  J e

 t




J w  
A
t
J e    
- Wirbelstromdichte
- Erregerstromdichte (eingeprägte Stromdichte)
42
 Differentialgleichungssystem:
1

A
rot rot A    
 Je
t


Satz von Stokes


1
rot Adl 


S


    A  J e dS


t


sinnvolle Vereinfachung:
planparalleler Fall:
S = ebene Fläche
 = Randkurve von S
J dS
J  J ( x , y)  e z ,
A  A ( x , y)  e z
B  rot A 


A
A
 ex 
 ey
y
x

A
1  A

 ex 
 e y dl 
  y
x

rotationssymmetrischer Fall: J  J (r, z)  e 
B



A
    t  e
S
z

 J  e z dS

A  A(r, z)  e
A
1  r  A 
 er 
 ez
z
r r
1  A
1 r  A  
 er 
 e z dl 

r r
  z


S
A


 e  J  e dS
 
t



Vorteil der Einführung des Vektorpotentials im 2D – Fall:
Vektorpotential hat nur eine Komponente 
 „skalares Potential“

verschiedene Möglichkeiten zur Berechnung der Integrale!
43
Herleitung der Differenzengleichungen
Diskretisierung und Differenzenapproximation
Diskretisierung:
1
rot Adl  ?



b

a

1
1 A
rot Ad l 
 e x  dx e x

 2 y

c
- regelmäßiges Gitternetz (rechtwinklig)
-  in der Masche konstant, gleich Wert im Maschenmittelpunkt
- J = konst. je Masche
- Integrationsweg: Seitenhalbierende zu Seitenhalbierende

1 A3  A0 x 0  x 2

 2 y3  y0
2

1  A

 e y   dye y


2  x
1
  rot Adl  
b

3
2

1
4

1 A 0  A 2 y0  y3

2
2 x 0  x 2
:
:
usw.

JdS  J 2  S2  J 3  S3  J 4  S4  J 5  S5  J 6  S6
 J2 
y3  y0 x 0  x 2

2
2
 A0 = A0 (A1, A2, A3, A4, (A), J, Geometrie)  Differenzenformel
großes, schwach besetztes, (nichtlineares) Gleichungssystem

weitere Lösung wie bei FDM !
Rand- und Grenzbedingungen, Zeitabhängigkeit
Erfassung von Grenzflächen
FDM: Unterscheidung zwischen Punkten in homogenen Feldbereichen und auf
Grenzflächen nötig! (Taylorreihenentwicklung !)
hier: -
unproblematisch, da stets gleiche Approximation der Integrale
gilt sowohl für Grenzflächen zwischen verschiedenen Materialien als auch
für Grenze zwischen Leiter – Nichtleiter
Voraussetzung:
Diskretisierung, so dass Eigenschaften je Element konstant sind!
44
Erfassung der Randbedingungen
1. Art:
A = konst. bzw. allgemein
2. Art:

d l  B  d l  rot A  0
(Rand = Feldlinie)
A
0
n
 Symmetriebedingung für A
n  B  n  rot A  0
( B  auf Rand)
Verfahrensweise wie bei FDM !
Behandlung der Zeitabhängigkeit
Zeitableitung des Vektorpotentials wird durch die Potentialwerte zweier aufeinanderfolgender
diskreter Zeitpunkte angenähert (Differenzenquotienten)
A
t

i , j, k

1
A i, j, k 1  A i, j, k
t

Ansatzverfahren für unregelmäßige Gitternetze
Ausgangspunkt:
Integraldarstellung für quasistationäres Feld, Rotationssymmetrie
(Berücksichtigung bewegter Teile!)

 

   

1
A


rot
A
dl
(
v
rot
A)  J e  d S







 
S  t



Rotationssymmetrie: J  J (r, z)  e 

A  A ( r, z)  e
1  A
1  r  A 

er 
 e z d l 

  z
r r

Diskretisierung
v  v(z)  ez
 J
w

 J i  J e dS
S
linearer Ansatz für A* = r A :
A*  a  br  cz
1  (r  A)
A
B  rot A  
 er 
 ez
r r
z

1  A*
A*
B 
 ez 
 er 

r  z
r

1
B   c  er  b  ez
r


Koeffizienten werden für jedes  aus den Knotenpotentialen ermittelt
 völlig analog zu FEM !
45
(J  dS)
 
j
j
j
 c j  b j   
  r  er  r  ez  d l    J j 3
j


Summation über alle j Dreiecke, die am Knoten i anliegen!
Zeitdiskretisierung:

1 *
A* A*
A  A alt *


t
t
t

A( t  0)
Wirbelstromterm:


A
A  A alt
dS   
dS
t
t

  A*
dS  A alt dS 
 

t  r






cz 
  a
dS  A alt dS
  b
r 
t   r



Berücksichtigung der Randbedingungen:
RB 1. Art:
A = 0 bei allen abgeschlossenen Feldgebieten (Außenraum feldfrei)
kein Beitrag zur rechten Seite der Integraldarstellung
inhom.:
A  0 bei nicht abgeschlossenen Feldgebieten
zusätzlicher Beitrag zum Umlaufintegral
 wird von der rechten Seite subtrahiert
RB 2. Art:
Berücksichtigung von Symmetrien in Rotationssymmetrie möglich:
A  0

r f (z)
auf Fläche r = konst.
A  0

z f (r )
auf Fläche z = konst.
46
Beispiel:
A
0
z
1
I

I
P1

P8
erfordert Berechnung eines speziellen Umlaufintegrals
A
1  A

 er 
 e z d l

r
r  z

1
1 A

dr  0

r z

dl  dr  e r
analog für P7  P8
 Rest wie oben !
inhom. RB:
A
 f (r )
z
f(r) in Integral I einsetzen und zum Umlaufintegral
addieren!
Gesamtgleichungssystem: - Ordnung = Zahl innerer Punkte + Randpunkte 2. Art
- Struktur des GS wie bei FDM oder FEM
47
2.2
Aufstellung und Lösung der Gleichungssysteme
Knotennummerierung und Indizierung
Standardindizierung:
parallel zu Koordinatenachsen mit m indizierten Knoten je Reihe
 verschiedene Bandbreiten BW
BW = 2m + 1
a) Zeilen mit m = 4

BW = 9
b) Spalten mit m = 3

BW = 7
Ermittlung der Bandbreite
BW = s + 1 + r
In einer Zeile gilt:
r = j – i,
r – Superdiagonale
s - Subdiagonale
s = i – j,
i – Zeilenindex
j – Spaltenindex
Einfachindizierung
P(i,j)  P(k): k = i + (j – 1) I
I – Zahl der inneren Knoten je Zeile
Abb.: 2D–Differenzenstern im
einfach indizierten Gitter
48
3D – Gitter
y – Richtung: 1  j  m
x – Richtung: 1  i  n
z – Richtung: 1  k  l
Pi,j,k:
Einfachindizierung:
Pq,r,s  Pt
mit:
t = (s – 1)n m + (q – 1) m +r
und
1 q  n
1 r  m
1 s  l
n – Anzahl y-z-Gitterebenen
m – Anzahl x-z-Gitterebenen
l – Anzahl x-y-Gitterebenen
Diagonalindizierung:
Rechteckgitter mit (I x J) – Gitterpunkten; I – Punkte in der Zeile
J – Punkte in der Spalte
Indizierung: - Start am linken unteren Gitterpunkt des Rechtecks
- Diagonalreihe für Diagonalreihe numerieren
a) J < I
 von links oben nach rechts unten
b) I < J
 von rechts unten nach links oben
Beispiel: I = 6, J = 5
Lösung der Gleichungssysteme
a)
direkte Verfahren :
- Gauß – Elimination
- Cholesky – Verfahren
b)
iterative Verfahren :
- Jacoby – Verfahren
- Gauß – Seidel – Verfahren
- Relaxationsverfahren
- Gradientenverfahren

Relaxationsverfahren für FDM besonders geeignet,
wenn der optimale Relaxationfaktor bekannt ist!
Dreieckszerlegung der Matrix:
A EDF
49
Iterationsformel:
x
x
( m 1)
 (1   ) x
( m 1)
Mx
(m)
(m)
  D (E x
1
( m 1)
 Fx
(m)
 b)
 ( E   1 D) 1 b
mit der Iterationsmatrix
M:

M ( )  ( E   1 D ) 1 F  (1   1 ) D

allgemeine Form des Iterationsverfahrens:
x
( m 1)
Mx
(m)
c
Optimaler Relaxationsfaktor 
Voraussetzungen an die Matrix:
positiv definit:
- symmetrisch
- positiv definit
- konsistent geordnet
(tridiagonal, blockweise tridiagonal)
symmetrische Matrix A mit reellen Koeffizienten ars,
deren quadratische Form
p
p
r 1
s 1
Q    ars  xr  xs
für jedes p- Tupel (x1, . . ., xp) positiv ist.
50
Relaxationsverfahren
lineares Gleichungssystem:
Ax  b
A  (ars ),
x  ( x1 ,..., x p )T
b  (b1 ,..., bp )T
Iterationsvorschrift:
arr ~
xr
xr
( m 1)
( m 1)
s 1
( m 1)
arr xr
r 1
  ars xs
 (1   ) xr
( m 1)
(m)
p
  ars xs( m )  br
s  r 1
( m 1)
 ~
xr
 (1   )arr xr
(m)
p
r 1
( m 1)
    ars xs
  ars xs( m )  br 
s  r 1

 s 1
= Punkt – SOR – Methode
Spezialfall für  = 1:
arr xr
( m 1)
Gauß – Seidel – Iteration
r 1
 br   ars xs
( m 1)
s 1
p
  ars xs( m )
s  r 1
Konvergenzbeschleunigung
Verringerung des Spektralradius 
µ - Eigenwert von
 ( M )  max
i
i

M
Relaxationsfaktor  so wählen, dass  möglichst klein wird!
Sind D r Diagonalmatrizen, so gilt:
2
betragsgrößter Eigenwert der Matrix
1 –
 opt 
12 
1
 D (E  F )
1  1  12
(     1) 2

Beziehung zwischen 1 und Spektralradius 
der Iterationsmatrix M
2
Vorgehensweise:
Differenzvektor:
d
( m 1)
x
( m 1)



Konvergenz für:
x
d
(m)
( m 1)
d
(m)
Bestimmung von 12
Bestimmung von 
opt
0<<2
 = 1 - Gauß – Seidel – Iteration
 > 1 - Überrelaxation
 < 1 - Unterrelaxation
51
Gradientenverfahren
Ax  b
lineares Gleichungssystem:
- reelle, positiv definite Matrix (m x m)
- Anfangsnäherung
- Iterationsindex
- Residuum
- Vektoren mit m Komponenten
A
x0
n
r
r, x, b, p
CG – Algorithmus (Conjugate Gradient Method)
r 0 : A x 0  b;
 1 : 1;
p 1 : 0;
n : 0
while residual > tolerance do
begin
 n : r n  r n
T
 n :
n
 n1
p n : r n   n   n 1
 n : p n  a  p n
T
 n :
n
n
r n1 : r n   n  A   n
x n 1 : x n   n   n
end
n : n  1
CGS – Algorithmus (Conjugate Gradient Squared)
CG nicht anwendbar!
A - nicht positiv definit 
 modifizierter Algorithmus (nach SONNEVELD, siehe Marsal /2-7/)
r 0 : A x 0  b; q 0 : q 1 : 0;  1 : 1; n : 0
while residual > tolerance do
begin
 : r T  r
00
n
n

 n : n
 n 1
u n : r n   n  q
n
p : u n   n  ( q   n  p
n
n
v n : A  p
n 1
)
n
 n : r T00  v n
 n :
q
n 1
n
n
: u n   n  v
r n 1 : r n   n  A  (u n  q
n 1
x n 1 : x n   n  (u n  q
)
n 1
)
n : n  1
end
52
Bandbreitenreduzierung (Algorithmus nach Cuthill/Mckee)

Umnummerierung aller Variablen (renumbering) führt zur Reduzierung der Bandbreite
und spart damit Speicherplatz!

Ziel

Minimierung K   D
i
i
mit: Di  max i  j jeder Zeile

d.h. Di
größter Abstand zwischen Diagonalterm der Zeile i
und jedem anderen Spaltenterm j dieser Zeile
 gebräuchlichstes Verfahren: Algorithmus von Cuthill/McKee
[Cuthill, E.;McKee, M. (1969):“Reducing the Bandwidth of Sparse Symmetric Matrices“,
ACM Proc. 24. Nat. Conf.; New York; vgl.: Hoole /10-9 /, S.222 – 224]
Beispiel: (8 x 8) – Matrix mit 20 NNE
2
1
1
1
3
4
5
2
2
3
3
0
4
5
4
5
0
0
0
7
6
10
7
0
8
6
7
0
8
6
0
9
0
0
11
0
12
0
13
0
14
0
15
16 17
0
18
0
19
0
8
20
Ausgangspunkt für die Umnummerierung ist die Darstellung der Verbindungen jedes Knoten
zu allen anderen Nachbarknoten.
 Aufbau der Tabelle:
Knoten
1
2
3
4
5
6
7
8
Zahl der
Verbindungen
3
4
3
2
3
3
2
4
Verbindung zu
neue Nummer
2,6,8
1,3,5,8
2,5,7
6,8
2,3,7
1,4,8
3,5
1,2,4,6
4
5
6
1
7
2
8
3
53
neue Verbindung
zu
5,2,3
4,6,7,3
5,7,8
2,3
5,6,8
4,1,3
6,7
1,2,4,5
Algorithmus:
1. Start mit dem Knoten mit den wenigsten Verbindungen.
Hier 4 (oder 7)  neue Nr. 1 in Spalte 4
2. Der mit Knoten 4 verbundene Knoten 6 (oder 8) wird Nr. 2 in Spalte 4,
Knoten 8 wird Nr. 3
3. Nun erfolgt das gleiche mit dem neuen Knoten 2 (alt: 6):
von den Verbindungen 1, 4, 8 sind 4 und 8 bereits nummeriert.
Folglich wird Knoten 1 die Nr. 4.
4. Fortsetzung dieser Prozedur für alle restlichen Knoten


Umkehrung dieses Algorithmus führt zu einer noch effektiveren Umnummerierung
Freie Wahl bei gleichrangigen Knoten führt auf unterschiedliche Strategien mit
unterschiedlichen Speicherplatzanforderungen.
 Modifizierungen sind also möglich!
5. Aufstellung der letzten Spalte:
Beispiel: neuer Knoten 4 (alt:1) hat Verbindungen zu 2, 6 und 8 gemäß Spalte 3
 Neue Verbindungen von Knoten 4:
5, 2, 3

5 (in Spalte 5)
Knoten
2 (in Spalte 1)

2
6

3
8
6. Neuordnung der Reihenfolge der Nummerierung  2, 3, 5
damit wird Nr. 5 über der Diagonale in die obere Dreiecksmatrix (symmetrisch)
“abgeschoben“ und entfällt somit für die Abspeicherung!
Es ergibt sich die folgende unsymmetrische Matrix:



1
2
3
1
2
3
1
2
4
4
5
6
7
3
5
6
4
5
0
0
7
0
8 9
10 11 12
6
7
0
0
0
0
0
0
0
0
13 14
15 16 17
8
0
0
0
0
0
8
18 19 20
Die Tabelle ist leicht zu programmieren
Dadurch entstehender Zusatzaufwand kann größtenteils kompensiert werden, wenn
Verkonditionierungen angewendet werden
(z.B. bei CG – Verfahren)
Einsparungen bei Speicherplatzreservierungen für die Matrix
Zusammenfassung:

Bevorzugte iterative Verfahren:
Gauß–Seidel–Verfahren
Relaxationsverfahren
Newton–Verfahren
Newton–Raphson–Verfahren
( insbesondere SOR )
( in vielen Varianten )
( häufig bei nichtlinearen FEM–Matrizen )
54
3
Finite – Difference Time – Domain Method (FDTD)
3.1
Entstehung der Methode
3.2
1D skalare Wellengleichung
2 f
t2
 c2
2 f
 x2
Lösungen:
f(x,t) = F1 (x – c t) + F2 (x + c t)
mit
c 
1

Taylorreihe für f(x,t) vom Punkt x0 zum Punkt x0 ± ∆x zum Zeitpunkt t :
f ( x  x, t ) 
f ( x, t )

f ( x  x, t ) 
 f ( x, t )
 2 f ( x, t ) x 2
x 
x
2
 x2
3
3
4
 f ( x, t ) x
 f ( x, t ) x 4

 ...
6
24
 x3
 x4
f ( x, t )

 f ( x, t )
 2 f ( x, t ) x 2
x 
x
2
 x2
3
3
4
 f ( x, t ) x
 f ( x, t ) x 4

 ...
6
24
 x3
 x4


Addition beider Ausdrücke:
f ( x  x, t ) 

 2 f ( x, t )
 x2

 2 f ( x, t ) 2
x
x 2
4
4
 f ( x, t ) x
 ....
12
x 4
f ( x  x, t )  2 f ( x, t ) 
 f ( x  x, t )  2 f ( x, t )  f ( x  x, t ) 


 x 2



 O x 
2

 „Zentrale – Differenzen – Approximation“ der 2. Ableitung.

Genauigkeit:
 2 f ( x, t )
t2
2. Ordnung,
Fehler ~ x 2

 f ( x, t  t )  2 f ( x, t )  f ( x, t  t ) 
2
 
  O t 
2
 t 


Diskrete Wellengleichung:


 f ( x, t  t )  2 f ( x, t )  f ( x, t  t ) 
2

  O t  
2



t




 f ( x  x, t )  2 f ( x, t )  f ( x  x, t ) 
2
c 2 
  O x 
2
 x 



55


Diskretisierung
Festlegungen:
xi
tn
fin
=
=
=
i Δx
n Δt
f (xi , tn )
Diskrete Wellengleichung:

f i n 1  2 f i n  f i n 1
 t 
2
 Ot    c 
2
2
f i n1  2 f i n  f i n1
 x 
2
 Ox  
2
Explizite Zeitschrittlösung für f:

 
n
 2 f i n  f i n1 
2 f
2
2
n
n 1
f i n 1  ct   i 1
  2 f i  f i  O x   O t 
2
x 




Stabilität und Genauigkeit der expliziten Lösung sind von den Werte Δx und Δt
abhängig!

„Magischer Zeitschritt“ :

Diskrete Wellengleichung mit „Magischem Zeitschritt“ :


Δx = c Δt .

f i n1  f in1  2 f i n  f in1  2 f i n  f i n1  f in1  f in1  f i n1

Analyse:
Mit
f i n  F1 i x  c n t 
g in  G 2 i x  c n t 
t  x / c
folgt
f i n1  F1 i  n  1x   f in1
g in 1  G 2 i  n  1x   g in1
Das ist die exakte Lösung!
56

3.3
2D – FDTD Lösung der Maxwellschen Gleichungen
Maxwell - Gleichungen:
Induktionsgesetz:
B
   E   E  J imp
t

B dS    E dl    E dS   J imp  dS
t 
S
C
S
S
Durchflutungsgesetz:
D
   H  M imp
t

D  dS   H  dl   M imp  dS
 t 
S
C
Gaußscher Satz:
B  0
D  
 D  dS     dV
S
V
 B  dS  0
S
Materialgleichungen:
D  E
B  H
J  E
Wirbelgleichungen
Aus dem Durchflutungsgesetz und dem Induktionsgesetz folgt:



 Bx  E z  E y


t
y
z
 Dx  H z  H y


 Jx
t
y
z
 By
 Dy
t

 Ex  Ez

z
x
 Bz  E y  E x


t
x
y
t

 Hx  Hz

 Jy
z
x
 Dz  H y  H x


 Jz
t
y
x
57
2D – Form der Maxwellschen Gleichungen
Fall 1:
TMz – Welle

 Bx  E z

t
y
 By
t
Fall 2:

(Hz = 0, Ez = Ez(x,y))
 Dz  H y  H x

 Jz

x
y
t
 Ez
x
TEz – Welle
 Dx  H z

 Jx
t
y
 Dy
 Hz

 Jy
t
x
(Ez = 0, Hz = Hz(x,y))

 Bz  E y  E x


t
x
y
1D – Form der Maxwellschen Gleichungen
Fall 1:
Fall 2:

TMz – Welle
(Hz = 0, Ez = Ez(x))

 Bx  E z

t
y
oder
 Dz  H y

 Jz
t
x
H x
1  Ez

t
 y
 Ez 1  H y 1
 Jz


t
 x
TEz – Welle
(Ez = 0, Hz = Hz(x))
 Dx  H z

 Jx
t
y
oder
 Ex 1  H z 1

 Jx
t
 y 
 Ey
 Bz

x
t
H z
1  Ey

t
 x
Modell der 1D Maxwell-Gleichungen ist identisch
mit dem der 1D-Leitungsgleichungen !
58
Der Yee – Algorithmus im 2D - TMz - Fall
TMz-Welle
Maxwell-Gleichungen:


 Bx  E z  E y


t
y
z
 By
t

(Hz = 0, Ez = Ez(x,y))
 Dz  H y  H x


 Jz
t
x
y
 Ex  Ez

z
x
Raumdiskretisierung:
xi = i Δx,
yi = j Δy
tn = n Δt
fi,jn = f (xi, yj, tn )
mit zentralen Differenzen:
f n1  f n1
 f  x, y , t 

x
i , j
2
x
i , j
2

 O x 
2

Maxwell-Gleichungen im 2D diskretisierten Raum (TMz )
j
H
y
i , j
1
2
Ez
i
1
1
, j
2
2
H
3.4

x
1
i , j
2
i
3D - FDTD - Lösung der Maxwell-Gleichungen ( YEE-Algorithmus )
Maxwell´s Wirbelgleichungen in kartesischen Koordinaten
59

Abbildung der Wirbelgleichungen auf den diskreten Raum
-




Definition eines regulären, orthogonalen Gitters
Eine Funktion f (x,y,z,t) wird in dem diskreten Gitter definiert und an den
Eckpunkten des Gitters berechnet:
f (x,y,z,t) = f (n ∆x, m ∆y, p ∆z, l ∆t) = flm,n,p
Zentrale – Differenzen – Approximation der Ableitungen
YEE – Zelle
(Primärgitter-Zelle)
Annahmen:
1)
Elektrische Feldvektoren sind parallel zur und
konstant entlang der Kanten des Primärgitters.
2)
Magnetische Feldvektoren sind normal zur und
konstant auf jeder Seitenfläche des Primärgitters.
3)
Magnetische Feldvektoren sind parallel zur und
konstant entlang der Kanten des Sekundärgitters.
4)
Elektrische Feldvektoren sind normal zur und
konstant auf jeder Seitenfläche des Sekundärgitters.
Die Sekundärgitterknoten verbinden die Zellmittelpunkte des Primärgitters.
60
Ableitung des YEE-Algorithmus aus den Maxwell-Gleichungen in Integralform

B  dS    E  dl
t 
S
C
mit dS


x dy dz folgt im diskretisierten Raum
1
1
l

z y  l  2
 l
l
l
2
y  E l zm , n , p  1 z 
B
B

x
x
1
1 z  E y
1 y  E z
1    E y
1
1
1

m ,n , p 
m ,n  , p 
m ,n  , p
m , n 1, p 
m , n  , p 1

t 
2
2
2
2
2
2
2
2



Multiplikation mit 1/∆z ∆y führt zu
B
l
1
2
x
1
1
m ,n  , p 
2
2
B
l
1
2
x
1
1
m ,n , p
2
2

t  l

  t  E l
l
l
E
E

y
y
z
1
1
1  E z
1
,
,
1
,
,
,
1
,
,
,
m
n

p

m
n

p
m
n

p

m
n
p


 y 
z 
2
2
2
2 
Analog folgt für eine Seitenfläche des Sekundärgitters
D
l
x
1
1
m , p
2
2
D
l 1
x
1
m ,n , p
2
1
1
1
1
l
l
l
 t  l  12

t  l  2
2
2
2

 H z m  1 , n  1 , p  H z m  1 , n  1 , p    H y m  1 , n , p  1  H y m  1 , n , p  1   J xm  1
y 

z
2
2
2
2
2
2
2
2
2,n , p



Ähnliche Approximationen ergeben sich für die restlichen Komponenten von B und D.
Stabilitätsverhalten

Kann über eine Von Neumann Analyse (wie im obigen Abschnitt) oder als direktes
Eigenwertproblem abgeleitet werden.

Explizite Lösungen sind stabil bei Verwendung der Courant-Schranke:
t
1

c

1
1
1
 2 2
2
x
y
z
Spezialfall:
∆x = ∆y = ∆z = ∆
∆t ≤ Δ / c √3
61
Gaußscher Satz

Damit der YEE-Algorithmus gut-gestellt ist, müssen die approximierten Felder auch
den Gaußschen Satz erfüllen. Tun sie dies nicht, treten „Geisterladungen“ auf, die zu
fehlerhaften Lösungen führen.

Es kann gezeigt werden, dass der Gaußsche Satz erfüllt wird, wenn jede Einheitszelle
separat betrachtet wird.

Elektrischer Fluss:
Gaußscher Satz:
 D  ds    dV  0
S
bei ladungsfreien Medien
V

D  ds  0
t 
S
Integration über die YEE-Zelle und aufsummieren der Seitenflächen
8
8


D

ds

D

ds




 H  dl  0
t 
i 1 t Si
i 1 Ci
S

Das Wegintegral des magnetischen Feldes entlang der Konturen, die die Zellflächen
beranden, hebt sich für jede Kante auf, so dass die rechte Seite verschwindet.

Da dies für alle zeitabhängigen Felder in einem quellenfreien Medium zutrifft, kann für
die diskretisierten Felder geschlussfolgert werden, dass der Gaußsche Satz in jeder
YEE-Zelle erfüllt ist.
 D  ds  0
SYEEZelle
Numerische Implementierung
Datenabspeicherung:
62
Inhomogene Medien
D x
H z H y

  Ex 
z
y
t
D y
t
  Ey 
H x H z

z
x
H y H x
D z
  Ez 

t
x
y

Stückweise homogenes Medium, dessen Grenzfläche mit den Kanten des Primärgitters
übereinstimmt.

Die 4 Bereiche, die das Gitter umgeben, sind beschrieben durch die Materialparameter
εi , σi , μ0 ( i = 1,2,3,4 )


Bild: Seitenfläche auf dem Sekundärgitter in einem inhomogenen Medium.
4 
 4 

   E  ds   E  ds    H  dl 

i
i
S
 
 i 1  C

i 1  t Si
i

 i

Si ist die Fläche auf jeder Unterfläche, die durch die Kontur Ci berandet wird.
Ausführen der Integration über jedes Si und die Berandung Ci
führt z.B. für den Bereich 1 zu:
 E 1n1  E 1n  
 E 1n1  E 1n  
  n dA 


1
 n dA   1 




2
t






1
1
1
1
n
n
n
n 

2
2
2
2
l 1  H 1  l 12  H 12  l 41  H 41  l 4  H 4 



n - Flächennormalenvektor
Wiederholung für die verbleibenden 3 Bereiche; Beachtung der Stetigkeit der
Tangentialkomponenten des elektrischen Feldes:
n
E 1 - elektrische Feld im Bereich 1,
n 
n 
n 
n 
E1  n  E 2  n  E 3  n  E 4  n

Addition der Resultate für alle 4 Bereiche:
 E 1n 1  E 1n  

  n         dA 
1
2
3
4


t


 E 1n 1  E 1n


2

 
  n         dA 
1
2
3
4


1
1
1
1
n
n
n
n 

2
2
2
2
l 1  H 1  l 2  H 2  l 3  H 3  l 4  H 4 


63

Wegen dA = A/4 können die Integrale als effektive Materialgrößen betrachtet werden
(Mittelwerte der 4 benachbarten Bereiche)
eff 
 eff 
1  2  3  4 
4
1   2   3   4 
4

Lineare Interpolation der Medien; im diskretisierten Raum ist das Medium nicht
tatsächlich stückweise konstant, sondern variiert eher linear über eine Diskontinuität.

Genauigkeitserhöhung durch Verwendung von Approximationen
2. Ordnung für die inhomogene Grenzfläche möglich.
YEE-Algorithmus in allgemeinen inhomogenen Medien
1
1
~ l
~ l
H xm ,2n , p  H xm ,2n , p 
~
~
E xl m1,n , p  E xl m ,n , p 
t
 m,n, p
t
 m ,n , p
~

E
z
~

H
z
l
ym , n , p 1
l
ym , n , p

~
 E yl m , n , p 

~
 H yl m ,n , p 1 
t
 m,n , p
t
 m ,n , p
~

E
y
~

H
y
~
 E zlm , n , p

~
 H zl m ,n 1, p

l
zm , n 1, p
l
zm , n , p

Berechnung des Mittelwertes von ε für jede Kante des Primärgitters;
Speichern εm,n,p

Berechnung des Mittelwertes von μ für jede Kante des Sekundärgitters;
Speichern μm,n,p
64