Tutorium

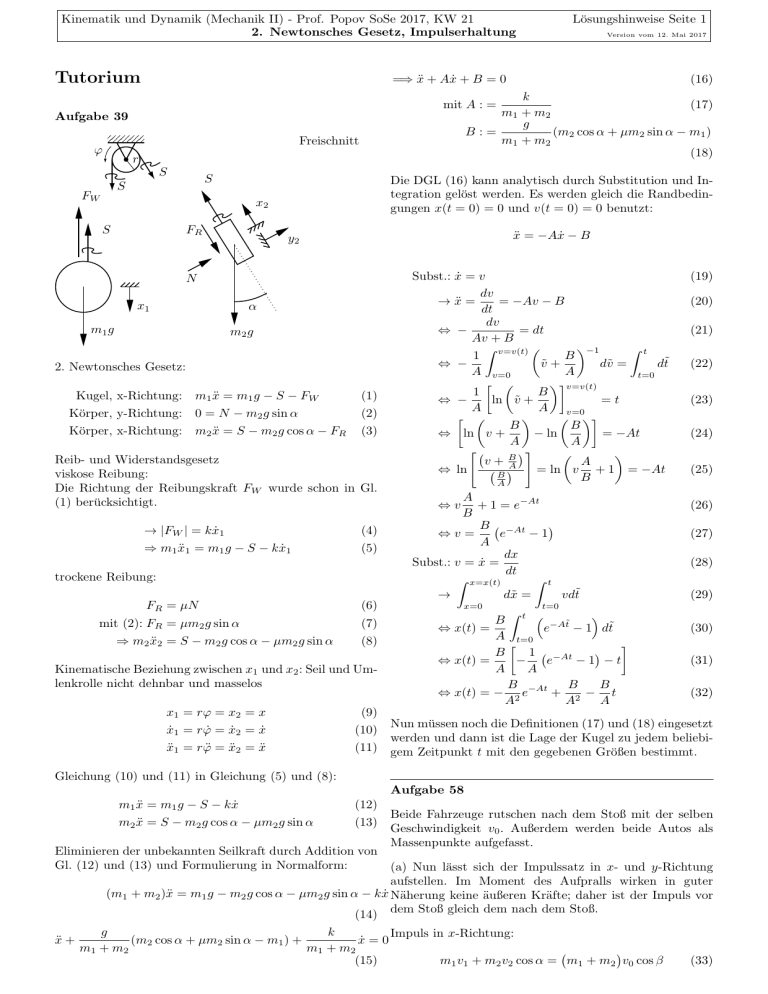
Kinematik und Dynamik (Mechanik II) - Prof. Popov SoSe 2017, KW 21
2. Newtonsches Gesetz, Impulserhaltung
Tutorium
Lösungshinweise Seite 1
Version vom 12. Mai 2017
=⇒ ẍ + Aẋ + B = 0
(16)
k
(17)
m1 + m2
g
B:=
(m2 cos α + µm2 sin α − m1 )
m1 + m2
(18)
mit A : =
Aufgabe 39
Freischnitt
ϕ
r
S
S
S
FW
Die DGL (16) kann analytisch durch Substitution und Integration gelöst werden. Es werden gleich die Randbedingungen x(t = 0) = 0 und v(t = 0) = 0 benutzt:
x2
S
FR
ẍ = −Aẋ − B
y2
N
x1
α
m1 g
m2 g
2. Newtonsches Gesetz:
Kugel, x-Richtung:
Körper, y-Richtung:
Körper, x-Richtung:
m1 ẍ = m1 g − S − FW
0 = N − m2 g sin α
m2 ẍ = S − m2 g cos α − FR
(1)
(2)
(3)
Reib- und Widerstandsgesetz
viskose Reibung:
Die Richtung der Reibungskraft FW wurde schon in Gl.
(1) berücksichtigt.
→ |FW | = k ẋ1
⇒ m1 ẍ1 = m1 g − S − k ẋ1
(4)
(5)
trockene Reibung:
FR = µN
mit (2): FR = µm2 g sin α
⇒ m2 ẍ2 = S − m2 g cos α − µm2 g sin α
(6)
(7)
(8)
Kinematische Beziehung zwischen x1 und x2 : Seil und Umlenkrolle nicht dehnbar und masselos
x1 = rϕ = x2 = x
ẋ1 = rϕ̇ = ẋ2 = ẋ
(9)
(10)
ẍ1 = rϕ̈ = ẍ2 = ẍ
(11)
Subst.: ẋ = v
dv
= −Av − B
→ ẍ =
dt
dv
= dt
⇔ −
Av + B
−1
Z t
Z
B
1 v=v(t)
dt̃
dṽ =
ṽ +
⇔ −
A v=0
A
t=0
v=v(t)
1
B
⇔ −
ln ṽ +
=t
A
A v=0
B
B
⇔ ln v +
− ln
= −At
A
A
"
#
v+ B
A
A
= ln v + 1 = −At
⇔ ln
B
B
A
A
+ 1 = e−At
B
B −At
⇔v=
e
−1
A
dx
Subst.: v = ẋ =
dt
Z t
Z x=x(t)
vdt̃
dx̃ =
→
t=0
x=0
Z
B t −At̃
⇔ x(t) =
e
− 1 dt̃
A t=0
B
1 −At
⇔ x(t) =
−
e
−1 −t
A
A
B
B
B −At
+ 2− t
⇔ x(t) = − 2 e
A
A
A
⇔v
(19)
(20)
(21)
(22)
(23)
(24)
(25)
(26)
(27)
(28)
(29)
(30)
(31)
(32)
Nun müssen noch die Definitionen (17) und (18) eingesetzt
werden und dann ist die Lage der Kugel zu jedem beliebigem Zeitpunkt t mit den gegebenen Größen bestimmt.
Gleichung (10) und (11) in Gleichung (5) und (8):
Aufgabe 58
m1 ẍ = m1 g − S − k ẋ
m2 ẍ = S − m2 g cos α − µm2 g sin α
(12)
(13)
Eliminieren der unbekannten Seilkraft durch Addition von
Gl. (12) und (13) und Formulierung in Normalform:
Beide Fahrzeuge rutschen nach dem Stoß mit der selben
Geschwindigkeit v0 . Außerdem werden beide Autos als
Massenpunkte aufgefasst.
(a) Nun lässt sich der Impulssatz in x- und y-Richtung
aufstellen. Im Moment des Aufpralls wirken in guter
(m1 + m2 )ẍ = m1 g − m2 g cos α − µm2 g sin α − k ẋ Näherung keine äußeren Kräfte; daher ist der Impuls vor
(14) dem Stoß gleich dem nach dem Stoß.
ẍ +
g
k
Impuls in x-Richtung:
(m2 cos α + µm2 sin α − m1 ) +
ẋ = 0
m1 + m2
m1 + m 2
(15)
m1 v1 + m2 v2 cos α = m1 + m2 v0 cos β
(33)
Kinematik und Dynamik (Mechanik II) - Prof. Popov SoSe 2017, KW 21
2. Newtonsches Gesetz, Impulserhaltung
Version vom 12. Mai 2017
Hausaufgaben
Impuls in y-Richtung:
m2 v2 sin α = m1 + m2 v0 sin β
(34)
Indem die beiden Formeln dividiert werden erhält man für
den gesuchten Winkel β:
tan β =
Lösungshinweise Seite 2
m2 v2 sin α
m1 v1 + m2 v2 cos α
(b) Zur Bestimmung der Rutschstrecke wird das zweite
Newtonsche Gesetz in Rutschrichtung gebildet:
−µ m1 + m2 g = m1 + m2 a .
Aufgabe 54
Das System hat einen Freiheitsgrad.
Der Körper 1 bewegt sich in einer Führung in vertikaler
Richtung. Für das Aufstellen der Bewegungsgleichung
kann man ihn daher wie eine Punktmasse behandeln.
Die Lage des Körpers 1 wird mit der Koordinate s
beschrieben (siehe Abbildung). Die Punktmasse 2 bewegt
sich auf einer Kreisbahn um den Punkt A. Daher soll die
Bewegung der Punktmasse 2 in Polarkoordinaten r, ϕ
beschrieben werden.
Für die Beschleunigung gilt also
a = −µg
.
y
(35)
Durch Trennung der Variablen erhält man
Z0
v0
und schließlich
ZXR
vdv =
−µgds
g
m1 g
N
m1
0
m2 g
v2
XR = 0
2µg
S1
(c) Zur Ermittlung der Geschwindigkeit der beiden Autos vor dem Zusammenstoß wird die Impulserhaltung aus
Aufgabenteil (a) herangezogen.
S1
m2
ϕ
S2
Zuerst wird v2 mit der Gleichung in y-Richtung (34) ermittelt:
m1 + m2 sin β
v2 =
·
v0
m2
sin α
√ m
km
≈ 76
= 15 2
s
h
Mit der Gleichung in x-Richtung (33) kann man nun v1
berechnen:
√
√
3
2
m1 + m2
m2
v1 =
·
v0 −
·
v2
m1
2
m1 2
√
m
km
≈ 79
= 30 3 − 1
s
h
x
A
Beide Stäbe übertragen nur Kräfte in Stabrichtung. Das
Newtonsche Grundgesetz in ϕ-Richtung lautet dann für
die Punktmasse 2
−S1 sin 2ϕ + m2 g sin ϕ = m2 lϕ̈ .
(36)
Für den Körper 1 liefert das Newtonsche Grundgesetz in
vertikaler Richtung
−m1 g − S1 cos ϕ = m1 s̈ .
(37)
Die Geschwindigkeit des Golf betrug also 79 km/h, die des
Eliminieren der Stabkraft S1 aus den Gleichungen (36)
Mercedes 76 km/h.
und (37) und Einsetzen der kinematischen Beziehung
s = 2l cos ϕ
liefert die gesuchte Bewegungsdifferentialgleichung
4m1 sin2 ϕ + m2 ϕ̈ + (4m1 sin ϕ cos ϕ) ϕ̇2
g
− sin ϕ (2m1 + m2 ) = 0 .
l
Aufgabe 57
Da keine äußeren Kräfte am System angreifen, bleibt der
Gesamtimpuls erhalten. D.h. der Impuls vor der Explosion
Kinematik und Dynamik (Mechanik II) - Prof. Popov SoSe 2017, KW 21
2. Newtonsches Gesetz, Impulserhaltung
gleicht dem Impuls nach der Explosion. Da der Impuls eine
vektorwertige Größe ist, müssen auch seine Komponenten
(z.B. für eine kartesische Basis) erhalten bleiben. Es gilt
also in horizontaler und in vertikaler Richtung (mit den
Abkürzungen cos(.) =: c(.) , sin(.) =: s(.) und tan(.) =:
t(.) ):
mv0 = m2 v2 cα2
0 = m 1 v 1 − m 2 v 2 s α2
(38)
(39)
Außerdem soll die Masse während der Explosion erhalten
bleiben:
m = m1 + m2
(40)
Diese drei Gleichungen sind die Bestimmungsgleichungen
für die drei gesuchten Größen m1 , m2 und v2 .
Aus (38) und (39) ergibt sich:
mv0
v2 =
m 2 c α2
m1 = m − m2
(41)
(42)
(41) und (42) können in (39) eingesetzt werden. Es folgt:
0 = (m − m2 )v1 − mv0 tα2
m2 = m(1 −
v0
tα )
v1 2
m2 wird nun in (40) und anschließend in (38) eingesetzt
und man erhält:
v0
m 1 = m t α2
v1
und
mv0 = m(1 −
v2 =
v0
tα )v2 cα2
v1 2
v0
cα2 − v0 /v1 sα2
Aufgabe 60
(a) Nach dem Abwurf von m1 + m2 mit der Relativgeschwindigkeit zum Boot w nach hinten, hat das Boot
die Absolutgeschwindigkeit va (nach rechts), und die abgeworfene Masse hat die Absolutgeschwindigkeit w − va
(nach links). Der Anfangsimpuls ist Null. Der Gesamtimpuls nach dem Abwerfen muss auch Null sein:
0 = (m0 − m1 − m2 )va − (m1 + m2 )(w − va )
Auflösen nach va liefert
va =
m1 + m 2
w
m0
(b) Analog erhält man für die Geschwindigkeit des Bootes
nach Abwurf der ersten Masse
m1
v b1 =
w
m0
Danach (mit dem Anfangsimpuls (m0 − m1 )vb1 ) wird die
zweite Masse m2 abgeworfen. Die Impulserhaltung liefert:
(m0 − m1 )vb1 = (m0 − m1 − m2 )vb − m2 (w − vb )
m
m2 1
⇒ vb =
+
w
m0
m0 − m1
Lösungshinweise Seite 3
Version vom 12. Mai 2017
Um mit dem ersten Aufgabenteil zu vergleichen, wird dies
umgeformt zu
m + m
m2
m2 1
2
vb =
−
+
w
m0
m0
m0 − m1
m + m
m 1 m2
1
2
w
+
=
m0
m0 (m0 − m1 )
m1 m2
= va +
w
m0 (m0 − m1 )
Für m0 > m1 ist die Geschwindigkeit des Bootes demnach
bei (b) größer als bei (a).