Lösung Übungsserie 7 (Bewegungen auf Bahnkurven in

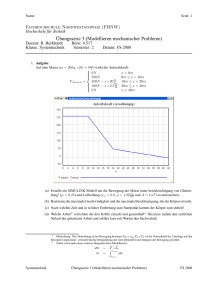
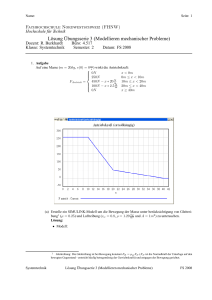
Name:
Seite: 1
Fachhochschule Nordwestschweiz (FHNW)
Hochschule für Technik
Lösung Übungsserie 7 (Bewegungen auf Bahnkurven in SIMULINK modellieren)
Dozent: R. Burkhardt ([email protected])
Büro: 4.517
Klasse: Systemtechnik
Semester: 2
Datum: FS 2008
1. Aufgabe
Eine Masse (m = 10kg) gleitet reibungsfrei auf der horizontalen Unterlage
p
−
→
r1 (p) =
p<0
0
m
mit der Schnelligkeit v0 = 8 s . Zum Zeitpunkt t0 = 0 kommt die Masse auf die Unterlage
p
−
→
r2 (p) =
p≥0
p2
auf der sie mit Reibung (Reibungskoeffizient μgleit = 0.1).
(a) Berechne den Krümmungsradius in Abhängigkeit vom Parameter p für p ≥ 0.
Lösung:
d−
→ 3
dp r2 (p)
ρ = →
→ d −
d2 −
r2 (p) × dp
dp
2 r2 (p)
1 3
2p = 0 1
2p × 2 s
3
1 + 4p2
=
2
(b) Skizziere die Bahnkurve für p ≥ 0. Bezeichne den Punkt auf der Bahnkurve für p = 1 und zeichne
die Kräfte ein, welche auf die Masse wirken, wenn sich die Masse in diesem Punkt in der
• Aufwärts- bzw. in der
• Abwärtsbewegung ist.
Lösung:
FR
FN
FG
Systemtechnik
FN
FR
FG
Lösung Übungsserie 7 (Bewegungen auf Bahnkurven in SIMULINK modellieren)
FS 2008
Name:
Seite: 2
(c) Erstelle ein SIMULINK Modell, mit dem sich die folgenden Fragen beantworten lassen:
• Zu welchem Zeitpunkt und an welchem Ort hat die Masse den höchsten Punkt erreicht?
• Wie schnell bewegt sich die Masse, wenn sie die krumme Bahn wieder verlässt?
Hinweis: Es ist einfacher, das SIMULINK Modell nur für den Zeitabschnitt während dem die Masse
auf der Bahn mit p ≥ 0 ist.
Lösung:
• Untersuchung Bahnkurve:
Tangentenvektor:
d−
1
→
r (p) =
2p
dp
=> Schnelligkeit (Parameterwechsel):
d−
s
→
= 1 + 4p2
r
(p)
dp
=> Richtung (Winkel):
y (p)
tan (ϕ) =
= 2p
x (p)
⇒
ϕ = a tan (2p)
• Kräfte:
=> Gewichtskraft:
−→
FG = mg
−−−−−→
−→
FG,norm = FG cos (ϕ) = mg cos (ϕ)
−−−−→
−→
FG,tan g = FG sin (ϕ) = mg sin (ϕ)
=> Normalkraft:
−→ −−−−−→ −→
mv 2
FN = FG,norm + FZ = mg cos (ϕ) +
ρ
=> Reibkraft:
−→ −→
FR = FN μG
=> resultierende Kraft (in Bewegungsrichtung):
−−−−→
dp −→
Fres = − FG,tan g − sign
FR = ma
dt
• Modell: siehe Beilage (m_serie7_aufgabe1.mdl ’’Modell’’ uns s_serie7_aufgabe1.m ’’Steuerungsskript’’).
• Graphen:
Systemtechnik
Lösung Übungsserie 7 (Bewegungen auf Bahnkurven in SIMULINK modellieren)
FS 2008
Name:
Systemtechnik
Seite: 3
Lösung Übungsserie 7 (Bewegungen auf Bahnkurven in SIMULINK modellieren)
FS 2008
Name:
Seite: 4
• Antworten:
=> Umkehrpunkt:
tumkehr
sumkehr
xumkehr
yumkehr
=
=
=
=
0.795s
3.066m
1.574
2.478
=> Endpunkt:
tend
= 1.639s
vend
= −6.055
2. Aufgabe
Gegeben sei die folgende Bahnkurve:
−
→
r =
−
→
r =
u
m
s
e−u
(a) Erstelle ein Simulink-Modell für die Bewegung der Masse (m = 1kg, x0 = −1m, y0 = 2.7183m,
v0 = 0 m
s ) wenn die Reibung vernachlässigt werden kann. Bestimme die Graphen für den zurückgelegten Weg, die Bahngeschwindigkeit und die Beschleunigung (in Bewegungsrichtung) in Abhängigkeit der Zeit.
Lösung:
• Geometrie der Bahnkurve:
u
e−u
−1
=
⇒ u0 = −1
e
• Startwert Parameter:
u0
−
→
r (u0 ) =
e−u0
• Tangentenvektor:
d −
1
→
r =
−e−u
du
Systemtechnik
Lösung Übungsserie 7 (Bewegungen auf Bahnkurven in SIMULINK modellieren)
FS 2008
Name:
Seite: 5
=> Schnelligkeit:
s
d −
−2u
→
r
du = 1 + e
=> Richtung (Winkel):
y (u)
= −e−u
tan (ϕ) =
⇒
ϕ = a tan −e−u
x (u)
• Krümmungsradius:
d−
3
→
r (u)
du
ρ = d−
→
d2 −
→
du r (u) × du2 r (u)
3
1
−e−u = 1
0
−e−u × e−u √
3
s
3
1 + e−2u
=
= eu 1 + e−2u
−u
e
• Physik (Kräfte und Bewegungsgleichung):
=> Gewichtskraft:
−→
FG = mg
−−−−−→
−→
FG,norm = FG cos (ϕ) = mg cos (ϕ)
−−−−→
−→
FG,tan g = FG sin (ϕ) = mg sin (ϕ)
=> resultierende Kraft (in Bewegungsrichtung):
−−−−→
Fres = FG,tan g = mg sin (ϕ) = ma
a = g sin (ϕ)
• Modell: siehe Beilage (m_serie7_aufgabe2a.mdl ’’Modell’’ uns s_serie7_aufgabe2a.m ’’Steuerungsskript’’):
• Graphen:
Systemtechnik
Lösung Übungsserie 7 (Bewegungen auf Bahnkurven in SIMULINK modellieren)
FS 2008
Name:
Seite: 6
(b) Bestimme den Graphen für die Auflagekraft (Normalkraft).
Lösung:
Siehe auch Beilage (m_serie7_aufgabe2b.mdl ’’Modell’’ uns s_serie7_aufgabe2b.m ’’Steuerungsskript’’)
(c) Erweitere dein Modell, in dem du Reibung berücksichtigst (μgleit = 0.2). Bestimme wieder die
Graphen für den zurückgelegten Weg, die Bahngeschwindigkeit und die Beschleunigung (in Bewegungsrichtung) in Abhängigkeit der Zeit.
Lösung:
Siehe auch Beilage (m_serie7_aufgabe2c.mdl ’’Modell’’ uns s_serie7_aufgabe2c.m ’’Steuerungsskript’’):
Systemtechnik
Lösung Übungsserie 7 (Bewegungen auf Bahnkurven in SIMULINK modellieren)
FS 2008
Name:
Seite: 7
(d) An welchem Punkt kommt die Masse zum stehen?
Lösung:
tend = 3.895s
xend = 9.529m
yend = 7.28 ∗ 10−5 m
Systemtechnik
Lösung Übungsserie 7 (Bewegungen auf Bahnkurven in SIMULINK modellieren)
FS 2008