Übungsserie 3 (Modellieren mechanischer Probleme)

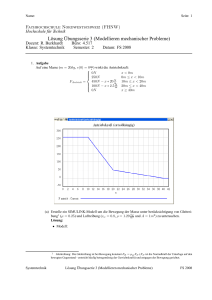
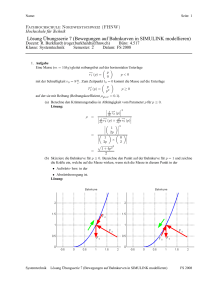
Name:
Seite: 1
Fachhochschule Nordwestschweiz (FHNW)
Hochschule für Technik
Übungsserie 3 (Modellieren mechanischer Probleme)
Dozent: R. Burkhardt
Klasse: Systemtechnik
Büro: 4.517
Semester: 2
Datum: FS 2008
1. Aufgabe
Auf eine Masse (m = 20kg, v(0) = 0 m
) wirkt die Antriebskraft:
⎧s
0N
x < 0m
⎪
⎪
⎪
⎪
250N
0m ≤ x < 10m
⎨
450N − x ∗ 20 N
10m ≤ x < 20m
FAntrieb =
m
⎪
N
⎪
⎪ 100N − x ∗ 2.5 m 20m ≤ x < 40m
⎪
⎩
0N
x ≥ 40m
(a) Erstelle ein SIMULINK-Modell um die Bewegung der Masse unter berücksichtigung von Gleitreikg
2
bung1 (μ = 0.25) und Luftreibung (cw = 0.8, ρ = 1.29 m
3 und A = 1m ) zu untersuchen.
(b) Bestimme die maximale Geschwindigkeit und die maximale Beschleunigung, die der Körper erreicht.
(c) Nach welcher Zeit und in welcher Entfernung zum Startpunkt kommt der Körper zum stehen?
(d) Welche Arbeit2 verrichten die drei Kräfte einzeln und gesamthaft? Skizziere zudem den zeitlichen
Verlauf der geleisteten Arbeit und erkläre kurz mit Worten den Sachverhalt.
1
Gleitreibung: Die Gleitreibung ist bei Bewegung konstant FR = μG FN (FN ist die Normalkraft der Unterlage auf den
bewegten Gegenstand - entsricht häufig betragsmässig der Gewichtskraft)) und entgegen der Bewegung gerichtet.
2 Arbeit (verwende einen weiteren Integrator beim Modellieren):
→
−
→ −
dW = F ◦ ds
send
W
=
dW
sstar
Systemtechnik
Übungsserie 3 (Modellieren mechanischer Probleme)
FS 2008
Name:
Seite: 2
2. Aufgabe
Ein Masse (m = 1kg) sei am einen Ende einer horizontalen Feder3 (k = 100 N
m ) angebracht. Auf der anderen
Seite der Feder sei ein Motor, welcher das zweite Ende in horizontaler Richtung auslenken kann:
xM = x sin (ωt)
(dabei bezeichnet x = 0.5m die Amplitude (maximale Auslenkung) und ω die Kreisfrequenz der Schwingung
(ω = 2πf )). Zum Startzeitpunkt sei die Feder entspannt und die Masse in Ruhe.
xM
x
M
(a) Erstelle ein SIMULINK-Modell um die Bewegung der Masse zu untersuchen (mit Einfluss von
Gleitreibung4 (μ = 0.3)).
(b) Bestimme den zeitlichen Verlauf der Auslenkung der Masse für ω 1 = 1.5 1s , ω 2 = 8.5 1s , ω 3 = 10 1s ,
ω 4 = 11.5 1s und ω 5 = 20 1s . Erkläre die gefundenen Resultate kurz.
3. Aufgabe
Gegeben sei die folgende Anordnung:
x0
x
Auf einem Tisch liegt ein Seil (mSeil = 1.5kg, lSeil = 2m). Zwischen dem Seil und der Tischoberfläche
wirken Reibungskräfte5 (μgleit = 0.15, μhaf t = 0.2).
(a) Bestimme alle Kräfte, welche auf das Seil einwirken und stelle die Bewegungsgleichung auf.
(b) Wie gross darf x0 (Anfangslänge des herunterhängenden Seilstücks) maximal sein, dass das Seil noch
nicht vom Tisch gleitet?
(c) Erstelle ein Modell um die Bewegungsgleichung numerisch zu lösen (x0 = 0.5m). Erzeuge die
Graphen x (t), v (t) und bestimme die Zeit bis das Seil ganz vom Tisch gerutscht ist.
(d) Bestimme die Reibungsarbeit.
3
Federkraft: Die (Rückstell-) Kraft der Feder ist direkt proportional zur Federauslenkung: FF = −k∆x
4 Beachte die Richtung der Gleitreibung!
5 Haftreibungskraft: Die Haftreibungskraft ist eine Zwangskraft (Kraft definiert sich an den Gegebenheiten):
FHaf t ≤ FN μhaf t
D.h. wenn die Masse sich nicht bewegt und die angreifende Kraft F < FN μhaf t kleiner der maximalen Haftreibung ist, ist die Haftreibung
gleich der angreifenden Kraft aber dieser entgegengesetzt!
Systemtechnik
Übungsserie 3 (Modellieren mechanischer Probleme)
FS 2008
Name:
Seite: 3
4. Aufgabe
Gegeben sei ein Fadenpendel:
ϕ
l
m
(a) Bestimme alle Kräfte, die auf die Masse einwirken (mit und ohne Luftwiderstand), und stelle die
Bewegungsgleichung auf.
(b) Erstelle das entsprechende Modell (m = 2kg, l = 1m, ϕ (0s) = ϕ0 =
π
4,
A = 10cm2 , cw = 0.5).
(c) Erzeuge die folgenden Graphen:
• ϕ (t)
• x (t), y (t) und y (x)
• Ekin (t), Epot (t) und Eges (t)
5. Aufgabe
Ein dünner Stab (mstab = 2kg, L = 1m) ist in der Mitte an einer vertikal angebrachten Schiene befestigt und
kann daran gleiten (μgleit = 0.2). Der Besfestigungspunkt sei mit einerr Feder (k = 500 N
m , lruhe = 1m) gegen
oben fest verbunden. Zudem kann sich der Stab um den Aufhängungspunkt frei drehen. Zum Startzeitpunkt
befindet sich die Anordnung in Ruhe und der Stab ist horizontal ausgerichtet. Nun wird am rechten Ende des
Stabes eine Masse (m = 5kg) angebracht.
y
x
ms
S
ϕ
m
(a) Bestimme alle Kräfte und Momente (bezüglich des Drehpunktes).
(b) Erstelle ein SIMULINK-Modell um die Bewegung des Systems zu untersuchen (Translation des
Schwerpunktes und Rotation um den Schwerpunkt).
(c) Skizziere den zeitlichen Verlauf für
• die Position des Schwerpunktes,
• und den Winkel ϕ
sowie die Bahnkurve die das rechte Stabende durchfährt.
Systemtechnik
Übungsserie 3 (Modellieren mechanischer Probleme)
FS 2008
Name:
Seite: 4
6. Aufgabe
In einem vertikal stehenden quadratischen Rahmen ist ein Massenpunkt (m = 10kg) mit vier identischen Federn
(k = 1kN/m, Ruhelänge der Federn l0 = 0.5m) befestigt:
(a) Erstelle ein Simulink-Modell um die Bewegung der Masse zu beschreiben (Anfangsbedingungen:
x(0) = 0.2, y(0) = 0.3, vx (0) = vy (0) = 0).
(b) Skizziere die Bahnkurve, auf welcher sich die Masse bewegt.
(c) Skizziere die Graphen für kinetische, potentielle, Federenergie und Gesamtenergie.
Systemtechnik
Übungsserie 3 (Modellieren mechanischer Probleme)
FS 2008