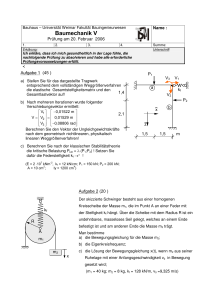
Aufgabe 1: Über eine reibungsfreie drehbare Rolle hängt ein Seil

Prof. Dr. Frank Nürnberg
Übung zur Physik 1
3. Blatt
Aufgabe 1: Über eine reibungsfreie
drehbare Rolle hängt ein Seil der Länge L
z
so, dass beide Seiten gerade L/2 lang sind.
Die Masse und der Radius der Rolle seien
vernachlässigbar. Das Seil hat die
M
Gesamtmasse M.
a.) Geben Sie die Bedingung für das
Kräftegleichgewicht an.
b.) Zur Zeit t=0 befinde sich die Seilmitte
genau bei z=0. Durch eine kleine
Schwankung entsteht ein Ungleichgewicht,
-L/2
so dass das Seil nach einer Seite abrollt.
Stellen Sie mit Hilfe des II. Newton’ schen
Axioms die Bewegungsgleichung für die im Seilmittelpunkt vereinigt gedachte Masse
M auf. (Drücken Sie hierzu die vom Übergewicht abhängige beschleunigende Kraft
als Funktion der z-Koordinate des Seilmittelpunktes aus.)
c.) Wie sieht die Bewegungsgleichung und deren Lösung z(t) für z<-L/2 aus?
d.) Zeigen Sie, dass der Ansatz z( t) = −L sinh( 2g L ⋅ t) die Bewegungsgleichung
erfüllt (sinus hyperbolicus ggf. in einer Formelsammlung nachschauen)
e.) Berechnen Sie die Zeit bis das Seil gerade ganz abgerollt ist.
f.) Mit welcher Geschwindigkeit v(t) bewegt es sich weiter?
g.) Mit welcher Beschleunigung a(t) = z(t) bewegt es sich weiter?
Aufgabe 2: Welche Richtung hat die Corioliskraft, wenn sich ein Körper auf der Erde
folgendermaßen bewegt:
a.) entlang des Äquators nach Westen
b.) auf dem Äquator senkrecht nach oben
c.) vom Äquator nach Norden
d.) Wie groß ist die Corioliskraft auf einen60 kg schweren Läufer, der am Nordpol
eine 100m Strecke in 12 sec bewältigt? Wie groß ist sie, wenn er die gleiche Strecke
zurückläuft?
Aufgabe 3: Am Äquator fällt ein Körper der Masse m= 1kg aus einer Höhe z=100 m
mit der Anfangsgeschwindigkeit v0=0 senkrecht nach unten (Fallturm).
a.) Welche Kraftwirkungen stellt ein Beobachter am Fuß des Fallturmes fest, wenn
die Bewegung der fallenden Masse
untersucht?
G G
G
b.) Geben Sie die Vektoren a(t),v(t) und r ( t) an.
c.) Wie groß ist die Abweichung des Auftreffpunktes von dem senkrechten Lotpunkt?
Aufgabe 4: Wieviele m³/min Wasser fließen durch die Turbinen eines 1 MW
Kraftwerks, wenn von der gesamten zur Verfügung stehenden potentiellen Energie
30% für Reibungsverluste und der restlichen kinetischen Energie des Wassers nicht
in elektrische Energie umgewandelt werden können. Der Wasserspiegel des
Stausees liegt 100 m über dem Kraftwerk.
Aufgabe 5: Ein PKW der Masse m fährt eine Passstrecke hinunter. Der Einfachheit
wegen nehmen wir einen mittleren Neigungswinkel von α = 7 o an. Der Wagen fahre
mit konstanter Geschwindigkeit v1.
a.) Welche mechanische Leistung P1 müssen die Bremsen aufnehmen und in Wärme
umwandeln, wenn die Geschwindigkeit konstant v1 sein soll?
b.) Auf welchen Wert v2 muß die Geschwindigkeit reduziert werden, wenn die
Bremsleistung von 10 kW nicht überschritten werden darf (technischer Hintergrund:
Scheiben- und Trommelbremsen würden sonst zu heiß werden)?
(v1=50km/h, m=1000kg)
E:\Texte\FH\Physik1\FH_PH1_N_3.doc
1