UE 4 - Bildungsportal Sachsen

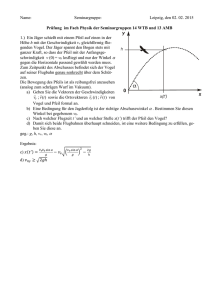
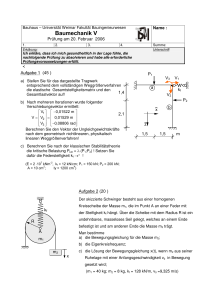
Übungsblatt für die 4. Übung am 22.11. bzw. 28.11.
Kontrollfragen:
1.) Welche Differentialgleichungen ergibt die Newton’sche Bewegungsgleichung
für
a) einen Federschwinger und für
b) einen Fallschirmspringer?
2.) Wie erhält man aus der Bewegungsgleichung die Ort(Zeit) - Funktion? Welche
Rolle spielen dabei Anfangsbedingungen?
3.) Wie klassifiziert man Differentialgleichungen?
4.) Wie unterscheidet man stabile, instabile und indifferente Gleichgewichte?
5.) Wie ist der Schwerpunkt oder Massenmittelpunkt definiert?
6.) Wie ist das Drehmoment definiert?
7.) Was besagt das Hebelgesetz? Begründen Sie es mit der Bewegungsgleichung
für die Drehbewegung!
8.) Welche Arten von Reibung gibt es?
Rechenaufgaben:
1.) Ein Sportler der Masse m = 70 kg springt von einem ruhenden Boot der Masse
M = 140 kg ab. Dabei lässt er über 0,5 s eine zeitabhängige Kraft F(t) = a +bt
mit a = 300 N und b = 400 N/s wirken. Wie groß sind nach dem Absprung
Impuls und Geschwindigkeit von Boot und Springer? Luft- und Wasserwiderstand seien vernachlässigbar.
2.) Ein Körper mit der Masse m1 befindet sich reibungsfrei auf einer geneigten
Ebene und ist durch ein Seil über eine Rolle mit einem frei hängenden Körper
der Masse m2 verbunden. (Tipp: Skizze anfertigen!)
a) Bei welchem Winkel der geneigten Ebene befindet sich das System im
Gleichgewicht? Es ist die dazugehörige Seilkraft anzugeben!
b) Bei welchen Winkeln der geneigten Ebene erfährt das System eine Beschleunigung vom Betrag . Wie groß sind dann die Seilkräfte? In welche
Richtung beschleunigt und in welcher Zeit nach dem Loslassen legt die
Anordnung eine Strecke s zurück? ( = 1,8 m/s2 , m1 = 400 g, m2 = 200 g)
c) Wie ändert sich die Beschleunigung bei Berücksichtigung eines Gleitreibungskoeffizienten µ = 0,1?
3.) In einem U-Rohr überall gleichen Querschnittes A steht eine Quecksilbersäule
der Länge l. Wird das U-Rohr kurz aus der Gleichgewichtslage gebracht,
beginnt die Quecksilbersäule zu schwingen.
a) Berechnen Sie die Schwingungsdauer T!
b) Errechnen Sie die Schwingungsdauer für eine gleichlange Wassersäule!
c) Wie lang ist ein mathematisches Pendel der gleichen Schwingungsdauer?
4.) Ein ideal biegsames, homogenes Seil der Masse M = 1 kg und der Länge
L = 2 m hängt um ein Stück l = 50 cm über eine Tischkante und beginnt
reibungsfrei zu gleiten. Nach welcher Zeit T verlässt das Seilende die
Tischkante?
(erhöhter Schwierigkeitsgrad)