Übungen zu Experimentalphysik I

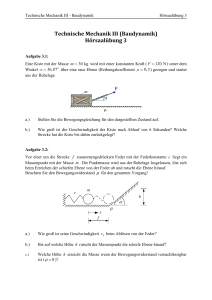
Übungen zu Experimentalphysik I
Prof. Dr. G. Abstreiter
Blatt 4
Ausgabe:
Besprechung:
7.11.2001
12.11. - 16.11.2001
WS 2001/02
Übungsgruppen:
Wochentag
Montag
Dienstag
Mittwoch
Donnerstag
Donnerstag
Donnerstag
Freitag
Freitag
Uhrzeit
10.15 – 11.45
8.15 – 9.45
8.15 – 9.45
12.15 – 13.45
12.15 – 13.45
12.15 – 13.45
8.15 – 9.45
12.15 – 13.45
Raum-Nr.
N1095
1601
2370
N0815
N0116
N0825
2100
N1070
Tutor
Karin Buchholz
Sebastian Luber
Ulrich Rant
Doris Heinrich (englisch)
Frank Fischer
Frank Ertl
Claus Ulbrich
Giovanni Tardini
Aufgabe 1: Rotierendes Fadenpendel
Die Masse m eines Fadenpendels (Fadenlänge r=1.60 m) soll an ihrem tiefsten Punkt
(Ruhelage) durch einen horizontalen Schlag so angestoßen werden, dass sie in einer
vertikalen Ebene um den Aufhängepunkt des Fadens rotiert. Die Bewegung soll als
reibungsfrei angenommen werden. Mit welcher Mindestgeschwindigkeit vunten ,min muss die
Masse den tiefsten Punkt ihrer Bahn verlassen, damit sie die Kreisbewegung ausführt ?
Aufgabe 2: Federpendel
Welcher Fehler ist in folgender Überlegung enthalten ?
Eine freihängende Feder reiche bis zum Punkt y=0. Nach Anhängen einer Masse m dehnt sich
die Feder infolge der Gravitationskraft mg. Gleichgewicht ist erreicht, wenn der Verlust an
potentieller Energie der Masse, mgy, gerade gleich dem Gewinn an potentieller Energie der
1
Feder ky 2 ist. Folglich gilt
2
mgy =
1 2
ky
2
und für die neue Ruhelage ergibt sich
y=
2mg
.
k
Aufgabe 3: Fadenpendel in bewegtem System
An einem Kranwagen hängt mit einem Seil der Länge l= 3 m eine Last senkrecht nach unten.
Der Wagen mit dieser Last fährt mit konstanter Geschwindigkeit v0= 5 m/s.
a)
Bis zu welchem Maximalwinkel schwingt die Last, wenn der Wagen abrupt durch einen
Aufprall gestoppt wird?
b) Welcher Auslenkwinkel ergibt sich, wenn der Wagen mit einer konstanten Verzögerung
von 2 m/s2 abbremst? Betrachten Sie hierfür das Kräftegleichgewicht im Grenzfall sehr
langer Verzögerungszeiten.
Aufgabe 4
Freier Fall mit Luftwiderstand
Auf einen Fallschirmspringer der Masse m = 75 kg wirkt eine Reibungskraft Fr, die
proportional zum Quadrat der Fallgeschwindigkeit v ist: Fr = kv2 mit der
Proportionalitätskonstante k = 0.29 kg/m (vor dem Öffnen des Fallschirms).
a) Welche Geschwindigkeit kann der Fallschirmspringer maximal erreichen, bevor er den
Fallschirm öffnet?
b) Stellen Sie die Bewegungsgleichung auf und bestimmen Sie durch Integration die
Geschwindigkeit des Fallschirmspringers v(t).
Hinweis:
∫a
2
1
1 a+x
für x < a , a > 0
dx =
ln
2
−x
2a a − x
c) Wie sieht die Bewegung für sehr kleine bzw. sehr große Zeiten aus?
d) Nach welcher Zeit erreicht der Fallschirmspringer 90% seiner Endgeschwindigkeit?
a)
Bestimmen Sie, ausgehend von der Bewegungsgleichung, v(t) numerisch:
Diskretisieren Sie dazu die Differentialgleichung in Zeitintervallen von ∆t = 1s (aus
den Differentialquotienten einer Ableitung werden dabei die Differenzenquotienten).
Stellen Sie die Beschleunigung a(t), die Geschwindigkeit v(t) und den Ort h(t) für eine
große Absprunghöhe h0 graphisch dar.
Aufgabe 5
Corioliskraft durch Erdrotation
a) Stellen Sie die Corioliskraft, die aufgrund der Erdrotation auf einen bewegten Körper
wirkt, in vektorieller Form dar.
b) Wie groß ist die Corioliskraft auf ein Flugzeug mit der Masse m = 10 t, das bei der
nördlichen Breite ϕ = 40° mit einer Geschwindigkeit v = 1900 km/h nach Norden fliegt?
In welcher Richtung zeigt diese Kraft?
c) Erklären Sie die Entstehung der Hoch- und Tiefdruckwirbel auf der Nord- und
Südhalbkugel.
d) Wo treffen alle auf der Erde ungestört fallenden Körper in Bezug auf den mit einem Lot
ermittelten Punkt auf?