1. Aufgabe (10 Punkte) Geben Sie die Definitionsgleichungen für

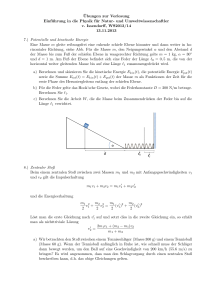
1. Aufgabe (10 Punkte)
Geben Sie die Definitionsgleichungen für folgende physikalische Größen an, und
erklären Sie die Formelzeichen:
elektrisches Feld, elektrisches Potential, potentielle Energie, elektrisches Dipolmoment, Hauptquantenzahl.
2. Aufgabe (8 Punkte)
Eine Masse m1 = 100 g gleitet reibungsfrei mit der Geschwindigkeit ~v1 = (0, 0, 1m/s).
Eine Masse m2 = m1 bewegt sich sich mit einer Geschwindigkeit von ~v2 = (0, 0, −3m/s)
auf die Masse m1 zu. Es kommt zu einem vollkommen inelastischen Stoß.
a) Welche Geschwindigkeit (Vektor!) haben die Massen nach dem Stoß?
b) Nach dem Stoß gleiten die Massen eine schiefe Ebene hoch. Welche Höhe erreichen sie?
3. Aufgabe (10 Punkte)
Bewerten Sie die folgenden Aussagen mit richtig oder falsch, und geben Sie eine
Begründung für Ihre Antwort. (Hinweis: Antworten ohne Begründung werden nicht
gewertet.)
a) Ein geostationärer Satellit über Aachen ist nicht möglich.(Hinweis: Der Satellit
verfügt über keinen eigenen Antrieb.)
b) Ein elektrischer Dipol befindet sich in einem homogenen elektrischen Feld. Sind
das Dipolmoment und der Feldvektor parallel zueinander, ist die potentielle Energie
minimal.
c) Totalreflexion findet nur statt, wenn ein Lichtstrahl von einem optisch dünneren
Medium in ein optisch dichteres Medium übergeht.
d) Für die molaren Wärmekapazitäten bei konstantem Druck (Cp ) bzw. bei konstantem Volumen (CV ) gilt: CV > Cp .
e) Die Wellenzahl ist eine materialunabhängige Konstante.
4. Aufgabe (2, 3, 2 Punkte)
Eine Masse von 4 kg hängt an einer Feder mit der Federkonstanten k = 200 N/m.
a) Wo befindet sich die Gleichgewichtslage y0 im Vergleich zur ungedehnten Feder?
b) Wie groß ist die Gesamtenergie des Feder-Masse-Systems, wenn die Feder um
zusätzlich 10 cm vertikal nach unten gedehnt wird? Nehmen Sie an, dass Epot = 0
ist bei y = y0 .
c) Welche Amplitude hat die Schwingung, wenn nach der Dehnung unter Teil b)
die Feder losgelassen wird und eine harmonische Schwingung vollzieht?
5. Aufgabe (8 Punkte)
Ein unendlich langer Vollzylinder mit dem Radius R ist homogen negativ geladen.
Die Volumenladungsdichte ist ρ. Geben Sie mit Hilfe des Gauß’schen Gesetzes (mit
Begründung Ihrer Rechenschritte) das elektrische Feld als Funktion vom Abstand
r von der Zylinderachse an für die Fälle:
a) innerhalb des Zylinders,
b) außerhalb des Zylinders.
6. Aufgabe (3, 5, 5 Punkte)
~
Ein Elektron mit einem Impuls p~ bewegt sich in einem homogenen Magnetfeld B.
a) Leiten Sie für eine reine Kreisbahn einen Ausdruck für den Bahnradius R des
Elektrons als Funktion seines Impulses her.
b) Skizzieren Sie für ein selbstgewähltes Beispiel (Richtung des Magnetfeldes)
die Kreisbahn des Elektrons, und tragen Sie mögliche Richtungen für folgende
Vektoren ein:
Lorentzkraft, Impuls, Drehimpuls, Winkelgeschwindigkeit, magnetisches Moment.
c) Welche der in Teil b) genannten Größen bleiben konstant, welche ändern sich?
(Begründung!)
7. Aufgabe (3, 2, 4 Punkte)
Der radioaktive Kern
235
92 U
zerfällt in Ruhe gemäß:
235
92 U
→
4
2 He
+
231
90 T h
(1)
a) Wie nennt man diesen Zerfall? Geben Sie zwei weitere Beispiele für radioaktive
Zerfälle an.
b) Welche Bedeutung haben die Zahlen von Gleichung (1)?
c) Bleiben bei diesem Zerfall der Impuls, der Drehimpuls, die kinetische Energie,
die Masse erhalten? (Begründung!)
D. Samm
Physikklausur 19. März 2015
2
8. Aufgabe (2, 4, 2, 3, 4 Punkte)
a) Erklären Sie die Lenz’sche Regel.
b) Durch welche thermodynamische Zustandsänderungen ist der Carnot’sche Kreisprozess charakterisiert?
c) Was ist der Photoeffekt?
d) Was ist ein ideales Gas?
e) Erklären Sie folgende Begriffe: Nukleon, Nuklid, Isotop, Halbwertszeit.
Konstanten
G = 6,67 ·10−11 N m2 /kg2
k = 1,38·10−23 J/K
R = 8,314 J/(mol K)
NA = 6,022 ·1023 mol−1
Ry = 1,097 ·107 m−1
e = 1,602·10−19 C
g = 9,81 m/s2
c = 2,998 ·108 m/s
h = 6,626 ·10−34 J s
h = 4,14 ·10−15 eVs
Elektronenmasse
me = 9,109 ·10−31 kg = 0,51 MeV/c2
Protonenmasse
mp = 1,673 ·10−27 kg ≈1 GeV/c2
Neutronenmasse
mn ≈1 GeV/c2
Elektrische Feldkonstante
ǫ0 = 8, 9 · 10−12 C2 /(N m2 )
Magnetische Feldkonstante µ0 = 4π10−7 N s2 /C2
Gravitationskonstante
Boltzmannkonstante
Gaskonstante
Avogadrokonstante
Rydbergkonstante
Elementarladung
Erdbeschleunigung
Lichtgeschwindigkeit
Plancksche Konstante
Umrechnungen
1 eV = 1,602 ·10−19 J
ϑ/◦ C = T /K - 273
D. Samm
Physikklausur 19. März 2015
3