5. Übungsblatt

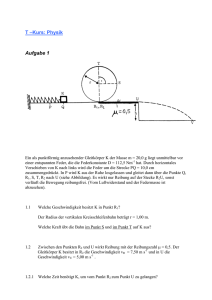
Proseminar zur Vorlesung Physik 1 (Mechanik und Wärme)
WS 2004/05
Alexander Altmeyer, Markus Bartenstein, Klaus Winkler, Matthias Theis
5. Übungsblatt, 08.11.2004
Präsenzübungen:
1. System von vier Massen. Betrachten Sie eine Anordnung von vier Massen in der
x, y-Ebene mit m1 = 2 kg, r1 = (−1, 1) m; m2 = 3 kg, r2 = (1, 1) m; m3 = 1 kg,
r3 = (−1, −1) m; m4 = 2 kg, r4 = (3, −1) m. Zeichnen Sie dieses Massensystem. Wo
liegt der Massenmittelpunkt ?
2. Kleine und große Billardkugel. Eine kleine Kugel mit Masse m und Geschwindigkeit v1 stoße zentral auf eine ruhende große Kugel der Masse M . Nach dem
vollständig elastischen Stoß bewege sich die große Kugel mit der Geschwindigkeit
v1 /5.
a) Welches Massenverhältnis M/m haben die Kugeln ?
b) Welche Geschwindigkeit v10 hat die kleine Kugel nach dem Stoß ?
3. Kugel, Stange und Feder. a) Eine Feder, die entspannt eine Länge l0 hat, wird
gedehnt (oder gestaucht) auf die neue Länge l. Geben sie die potentielle Energie
Epot an, die in der Feder steckt.
b) Nun sei diese Feder mit eine Kugel der Masse m = 2 kg verbunden, die sich
reibungslos eine vertikale Stange entlang bewegen kann (siehe Zeichnung). In der
Ausgangslage (A) ist die Feder entspannt und hat eine Länge von l0 = 3 m. Die
Federkonstante soll κ = 22 N/m betragen. Die Kugel werde losgelassen und erreiche
einen d = 4 m tieferen Punkt (B). Welche Geschwindigkeit vB hat sie dort ?
c) Was passiert, wenn man Federn mit einer anderen Federkonstante κ (gleiche
Länge l0 ) verwendet ? Geben Sie vB (κ) an und zeichnen Sie den Verlauf. Bei welcher
Federkonstante wird der Punkt B gerade noch erreicht ?
Hausübungen: (Abgabe: Mo. 22.11.2004, 12:15h, das ist die Woche nach dem
Test! Der Inhalt dieser Aufgaben wird nicht für den Test benötigt.)
1. Inelastischer Stoß. Ein Geschoß der Masse m werde mit einer Geschwindigkeit v0
auf einen anfänglich ruhenden Klotz der Masse M geschossen und bleibe in diesem
stecken.
a) Welche Geschwindigkeit v1 hat der Klotz nach Auftreffen des Geschosses ?
b) Welche kinetische Energie Ekin; 1 hat der Klotz mit dem darin steckenden Geschoss
nach dem Stoß ? Wie verhält sich diese zu der kinetischen Energie des Geschosses
vor dem Stoß ? (Ekin; 1 /Ekin; 0 = ?)
c) Wie groß ist also der Energieanteil ∆E, der in dem inelastischen Stoß in andere
Energieformen umgewandelt wird ? Um welche anderen Energieformen handelt es
sich dabei ?
Bemerkung: Überlegen Sie sich zunächst, welche Erhaltungssätze bei inelastischen
Stössen gelten und informieren Sie sich gegebenfalls in einem Physikbuch!
2. Drehimpuls bei gleichförmiger Bewegung. Eine Punktmasse m bewege sich
gleichförmig mit konstanter Geschwindigkeit v auf der Bahn r(t) = r0 + vt.
a) Geben Sie den Drehimpuls L bzgl. des Koordinatenursprungs als Funktion der
Zeit an.
b) Welche Bedingung muss eine an m angreifende Kraft F erfüllen, damit diese den
Drehimpuls nicht ändert.
3. Masse am Faden und Rohr. Bemerkung: Informieren Sie sich zunächst in einem
Physikbuch über Drehbewegungen, insbesondere über die Begriffe Drehimpuls und
Drehmoment sowie deren Zusammenhang!
In dem gezeichneten System kreise eine Masse m an einem Faden, der durch ein
Rohr geführt wird. Zunächst bewege sich die Masse mit der Geschwindigkeit v0 auf
einer Kreisbahn mit Radius r0 . Der Radius der Kreisbahn werde nun auf r reduziert.
a) Warum bleibt der Drehimpuls dabei erhalten ?
b) Welche Geschwindigkeit hat die Masse beim Radius r ?
c) Welche kinetische Energie hat die Masse vor und nach Reduktion des Umlaufradius ? Wie groß ist die Änderung ?
d) Berechnen Sie die bei der Reduktion des Bahnradius verrichtete Arbeit durch
das entsprechende Wegintegral der Kraft.
e) Vergleichen Sie die Ergebnisse von c) und d).