C V F CU Q - treminer.de

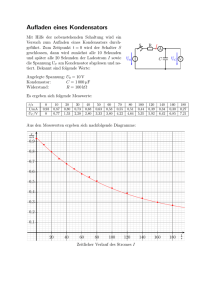
Aufgaben zum elektrischen Feld
Aufgabe 1 - Größenbeziehungen im elektrischen Feld
E  1,79 10  3 N
C
q  1,5 10  4 C
2
2
gegeben: r  5,0 10 m
gesucht: Kraft der Kugel
Lösung:
F
E
 F  q2  E
q2
N
 2,69 10 7 N
C
Berechnung der felderzeugenden Ladung
1
qq
F
 1 22
40 r
Auflösen nach q1
F  1,5 10  4 C 1,79 10 3
40 r 2
q1 
F
q2
Einsetzen der Daten:
q1 
4  8,85 10 12
C2
Nm 2
 (5,00 10 2 m) 2
1,5 10 4 C
 2,69 10 7 N
q1  5,0 10 16 C
Aufgabe 2 - Bandgenerator
s 0,032m
tan   
 0,09    5,14
l
0,35m
F
tan   E  FE  mg  tan 
FG
Einsetzen der Daten liefert:
N
FE  10,0 10 3 kg  9,81
 tan( 5,14)  8,82 10 3 N
kg
Berechnung der elektrischen Feldstärke der
Bandgeneratorkugel:
F 8,82 103 N
1 N
F  q2 E  E 


4
,
41

10
q2 2,00 10 2 C
C
Verbesserung der Hausaufgabe:
Aufgabe 3a
D=0,10 N/m
-3,00 nC
Kraftwirkung
ungleichartige Ladungen anziehen.
b) Berechnung der elektrischen Feldstärke:
N
0,10  0,0300 m
F Ds
m
E


q
q
3,00 10 9 C
N
E  1,0 10 6
C
c) Änderung der elektrischen Feldstärke bei gleicher
Kraftwirkung und doppelten Abstand:
E 
tan  
FE
 FE  mg  tan 
FG
FE  0,010kg  9,81
N
 tan( 3,9)  6,7 10 3 N
kg
Aufgabe 3b
E
FE
q Kugel
6,7 103 N
N
3 N


2680

2
,
7

10
2,50 106 C
C
C
Weitere Aufgaben
Aufgabe 1
a) Aufgrund der anziehenden Kraftwirkung muss die BandGeneratorkugel positiv geladen sein, weil sich
QBandgenera torkugel
4 0  r 2
Da die elektrische Feldstärke zum Quadrat des Abstandes
indirekt proportional ist, würde die elektrische Feldstärke
bei doppeltem Abstand auf ein Viertel sinken.
Damit die Kraftwirkung konstant bleibt, muss man die
elektrische Feldstärke vervierfachen.
Verbesserung der Hausaufgabe
Blatt Aufgabe 2
a) Berechnung der Kraft, durch die das Abstoßen verursacht
wird.
FE  mg  tan 
N
FE  0,100 kg  9,81
 tan 5,00 
kg
FE  0,085 N
b) Berechnung der Feldstärke des Generators:
E
Versuch:
An einem Plattenkondensator werden die Platten
auseinandergezogen und dabei die Spannung gemessen:
F
0,085 N
7 N


1
,
14

10
q 7,50 109 C
C
c) Gemäß Formel gilt für radialsymmetrisches Feld:
E
1.6 Spannung und Potential im homogenen Feld
Q
40 r
2
Damit ist die elektrische Feldstärke direkt proportional zur
felderzeugenden Ladung Q. Somit muss man die Kugel des
Bandgenerators doppelt so stark aufladen, damit man die
doppelte Feldstärke erzielt. Dies wird durch eine höhere
Geschwindigkeit des rotierenden Bandes realisiert.
U
Beobachtung:
Die Spannung ist direkt proportional zum Abstand der
Platten.
Erklärung:
Durch das Auseinanderziehen der Platten wird Arbeit
geleistet.
W  FE  s
W  qEs
Andererseits gilt für die elektrische Leistung:
P  UI
Da Arbeit das Produkt aus Leistung und Zeit ist, folgt
weiter:
W  U  I t
W U q
Damit ergeben sich für die Arbeit zwei Beschreibungen:
W  q U
W  qEs
 U  E  s
Da E aufgrund des homogenen Felds konstant ist ergibt sich
also eine direkte Proportion zwischen der Spannung U und
dem Abstand s.
Zusammenfassung:
Die elektrische Arbeit in einem homogenen elektrischen
Feld wird beschrieben durch:
W  qEs
Dabei beschreibt s die Länge der Verschiebungsstrecke.
Zur Spannung U, die zwischen den beiden Platten gemessen
wird besteht die Beziehung
U  Es
Kapazität des Kondensators (Fortsetzung)
Versuch 2:
Die am Kondensator anliegende Spannung wird auf 200 V
fest eingestellt. Der Abstand der Platten zueinander wird
durch Abstandhalter verdoppelt bzw. verdreifacht.
Im Anschluss wird die Ladung mit Hilfe einer Messsonde
an der positiven Kondensatorplatte abgegriffen.
Es ergibt sich folgende Messtabelle: (siehe Nebenseite)
Ergebnis:
Der Graph im Diagramm ist ein Hyperbelast
=> die Ladung des Kondensators ist indirekt proportional zu
dem Abstand der Kondensatorplatten.
=> da U=konstant gewählt wurde ändert sich die Kapazität
im gleichen Maße wie die Ladung des Konden- sators.
=> Die Kapazität des Kondensators ist indirekt proportional
zum Abstand der parallelen Kondensatorplatten.
Gedankenexperiment:
Bei konstanter Spannung U und gleichem Abstand der
Kondensatorplatten wird ein Kondensator mit doppelter
Kondensatorfläche mit einem Kondensator mit einfacher
Fläche verglichen.
Postulat:
Die Flächenladungsdichte wird konstant gehalten.
Q
   Q    A
A
Entwicklung der Kondensatorladung bei doppelter
Kondensatorfläche:
A1  2  A
 Q1    2 A  2  A  2Q
Q
2Q
Q
 C1  1 
 2  2C
U
U
U
Bei doppelter Kondensatorfläche verdoppelt sich die
Kapazität des Kondensators.
Verallgemeinerung auf die n-fache Kondensatorfläche:
Qn    n  A  n  Q
nQ
Q
 Cn 
 n
 nC
U
U
Die Kapazität eines Kondensators ist direkt proportional zur
Fläche der Kondensatorplatten.
Zusammenfassung:
C ist indirekt proportional zu d.
1
C ist direkt poroprtional zu d
C ist direkt proportional zu A.
___________________________________
Insgesamt:
A
C ist direkt proportional zu d
Merksatz:
Die Kapazität C eines Plattenkondensators mit der
Kondensatorfläche A und dem Plattenabstand d wird
bestimmt durch:
A
C  0 
d
Bemerkung:
Mit einem sogenannten Dielektrikum wird die Ladungsdichte um einen Faktor  r erhöht. Dieser wird als
Permittivität bezeichnet.
Q   r    A   r  Q0
 Q
A
 C  r 0   r  C0   r  0 
U
d
2.2 Die Energie eines Kondensators
Das U-Q- Diagramm eines Kondensators:
Q
Herleitung der vom Kondensator aufgenommenen Energie
in einem Spannungs-Ladungs- Diagramm
Erstes Beispiel: Elektrische Energie:
Q
Steigung: Kapizität C
Q0
Q0=C*U0
Q0
U
U0*Q0
U0
Dreiecksfläche stellt die im Kondensator
U
U0
Erkenntnis:
Eel  U 0  Q0
Die elektrische Energie ist in dem U-Q-Diagramm der
Flächeninhalt unter dem Graphen.
gespeicherte Energie dar.
Ziel: Flächeninhalt dieses Dreiecks soll berechnet werden:
1
1
1
EKon  Q0 U 0  C U 0 U 0  C U 02
2
2
2
Merksatz:
Ein Plattenkondensator mit der Kapazität C, an welchem die
Spannung U anliegt, besitzt die Energie
1
Ekon  C  U 2
2
2.3 Elektrische Schaltungen von Kondensatoren
Zur Parallelschaltung zweier Kondensatoren:
I1
Grundwissen:
Es gibt grundlegend zwei Schaltungstypen:
Parallelschaltung
Serienschaltung (Reihenschaltung)
In der Parallelschaltung gilt:
U  konstant
I  I1  I 2
In der Reihenschaltung gilt:
U  U1  U 2
I  konstant
C1
I2
C2
U
Ziel: Bestimmung der Gesamtkapazität der Schaltung
Q It I1  I 2 t I1t  I 2t I1t I 2t
C





U U
U
U
U
U
Q Q
 1  2  C1  C2
U 
U

C1
C2
Merksatz:
In einer Parallelschaltung von Kondensatoren addieren sich
die einzelnen Kapazitäten zur Gesamtkapazität:
C  C1  C2
Zur Reihenschaltung von Kondensatoren
C1
C2
U1
U2
Ziel: Bestimmung der Gesamtkapazität der Schaltung
1 U U1  U 2 U1 U 2
 


C Q
Q
Q 
Q

1
C1
1
C2
Insgesamt:
1
1
1
C  C1


 2
C C1 C2
C1C2
Bildung des Kehrwerts auf beiden Seiten:
C1C2
C
C1  C2
Kapazität einer Reihenschaltung
Die Entladung eines Kondensators
Versuchsaufbau:
Ur
R
U
Uc
Aufladekreis
Entladestromkreis
Zur Auswertung wird das Messgeräts des Versuchs gefilmt.
Ergebnis:
Die Spannung fällt beim Entladen des Kondensators
exponentiell mit der Zeit t ab.
=>
U  U0  e
 k t
Ziel: Bestimmung der Konstanten k in der Gleichung
Auswertung des Versuchs:
Reihenschaltung von Kondensator und Widerstand
U  UC U R
Q
U   RI
C
Q
Q
U   R
C
t
Im Fall der Entladung gilt: U=0. Damit ergibt sich folgende
Gleichung:
Q
Q
 R
0
C
t
Auflösen der Gleichung nach Q
Q
Q  
 t
CR
Differentialgleichung für die Entladung eines Kondensators.
Die Gesamtladung des Kondensators wird beschrieben
durch:
Q(t )
Q(t  t )  Q(t ) 
 t
CR
Ladung zur Zeit t=0 (d.h. die Gesamtladung)
U=6,5 V
C= 50 nF
R  1,7 107 
t  0,100 s
________
Berechnung von Q:
9
7
Q  CU  50 10 F  6,5V  3,3 10 C
________
3,3 107 C
Qges (0,1s )  3,3 10 C 
 0,1s
50 109 F 1,7 107 
7
Qges (0,1s )  2,91107 C
____
2,91107 C
Qges (0,2s)  2,9110 C 
 0,1s
50 109 F 1,7 107 
7
Qges (0,2s)  2,57 107 C
____
Berechnung der Spannung, die bei der Entladung anliegt:
Q
Q
C
 U 
U
C
Für die Spannung ergibt sich folgende Näherungsformel
Q(t )
Q(t )
U (t  t ) 
 C  t
C
CR
Die exakte Lösung erfolgt wegen der zugrunde liegenden
Differenzialgleichung folgendes Aussehen:
U (t )  U 0  e

t
CR
Entladungsspannung des Kondensators
Zusammenfassung: Gesetze des Kondensators
Folgende Gesetze beschreiben den Kondensator:
Definition der Kapazität:
Q
C
U
Kapazität eines Kondensators mit Fläche A und Abstand d:
A
C  0 
d
Kondensator mit Dielektrikum:
A
C   r 0 
d
Energie eines Kondensators:
1
E  CU 2
2
Entladungsspannung eines Kondensators:
U (t )  U 0  e

t
RC
4.2 Die magnetische Flussdichte
Versuchsbeschreibung:
Eine Leiterschleife der Länge l wird in ein Magnetfeld
gehalten. Die Leiterschleife ist an einer Waage befestigt, die
sich im Gleichgewicht befindet. Wird die Leiter- schleife
mit Strom durchflossen, dann übt das Magnet- feld eine
Kraft auf die Leiterschleife aus. Diese kann man dann durch
das Austarieren der Waage messen.
Messreihe 1:
Bei konstante Länge der Leiterschleife wird die Stromstärke
variiert.
Messreihe 2:
Bei konstanter Stromstärke I wird die Länge der
Leiterschleife variierte
´
Ergebnis von Messreihe 1:
Die magnetische Kraft F ist direkt proportional zur
Stromstärke, die durch die Leiterschleife fließt.
Ergebnis Messreihe 2:
Die Kraft ist direkt proportional zur Länge der
Leiterschleife.
Damit gilt insgesamt:
𝐹
= konstant
𝐼∙𝑙
Definition:
Der Quotient aus der bewirkten magnetischen Kraft auf
einen Leiter der Länge l, der mit der Stromstärke I durchflossen wird, bezeichnet man als magnetische Flussdichte.
𝐹
𝐵=
𝐼∙𝑙