Kinematik - Definitionen Aufgabe 3: Massenerhaltung

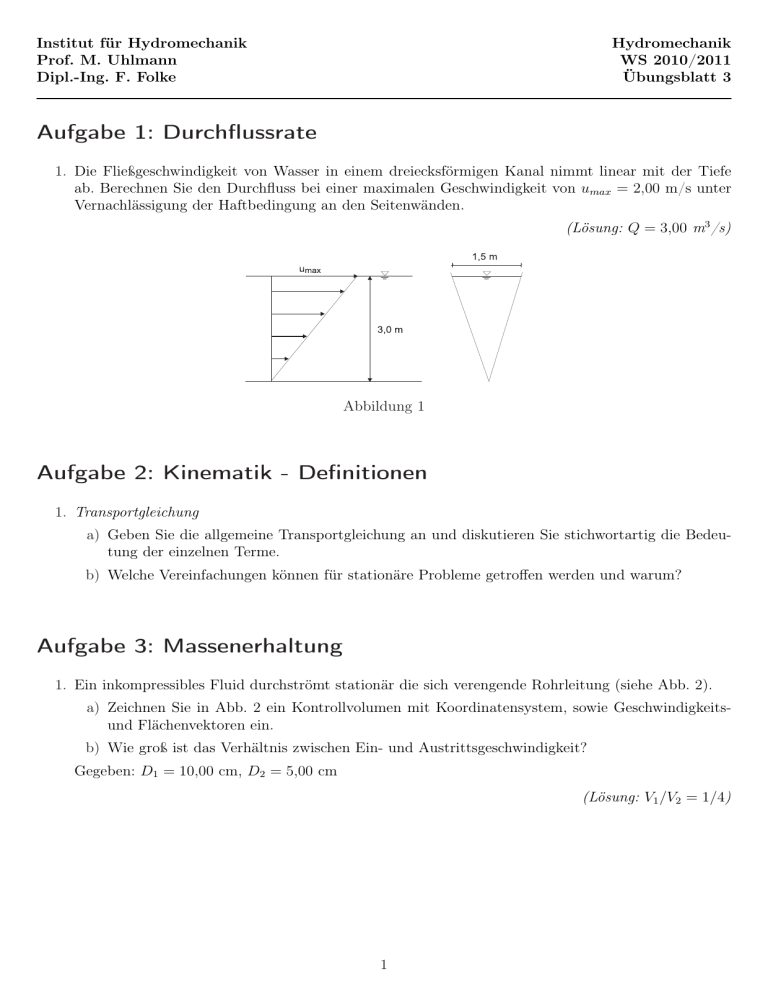
Institut für Hydromechanik
Prof. M. Uhlmann
Dipl.-Ing. F. Folke
Hydromechanik
WS 2010/2011
Übungsblatt 3
Aufgabe 1: Durchflussrate
1. Die Fließgeschwindigkeit von Wasser in einem dreiecksförmigen Kanal nimmt linear mit der Tiefe
ab. Berechnen Sie den Durchfluss bei einer maximalen Geschwindigkeit von umax = 2,00 m/s unter
Vernachlässigung der Haftbedingung an den Seitenwänden.
(Lösung: Q = 3,00 m3 /s)
Abbildung 1
Aufgabe 2: Kinematik - Definitionen
1. Transportgleichung
a) Geben Sie die allgemeine Transportgleichung an und diskutieren Sie stichwortartig die Bedeutung der einzelnen Terme.
b) Welche Vereinfachungen können für stationäre Probleme getroffen werden und warum?
Aufgabe 3: Massenerhaltung
1. Ein inkompressibles Fluid durchströmt stationär die sich verengende Rohrleitung (siehe Abb. 2).
a) Zeichnen Sie in Abb. 2 ein Kontrollvolumen mit Koordinatensystem, sowie Geschwindigkeitsund Flächenvektoren ein.
b) Wie groß ist das Verhältnis zwischen Ein- und Austrittsgeschwindigkeit?
Gegeben: D1 = 10,00 cm, D2 = 5,00 cm
(Lösung: V1 /V2 = 1/4)
1
Abbildung 2
2. Beide Kolben aus Abb. 3 bewegen sich nach links, Kolben A doppelt so schnell wie der Kolben B.
Welche der folgenden Aussagen ist korrekt? (Begründung)
Der Wasserspiegel im Behälter
a) steigt; b) ändert sich nicht; c) fällt.
Durchmesser=2m
Durchmesser=1m
Abbildung 3
3. Gegeben ist das in Abb. 4 skizzierte T-Stück mit kreisförmigen Querschnitt. Bestimmen Sie die
Geschwindigkeit V3 .
Gegeben: V1 = 6,00 m/s, V2 = 4,00 m/s, D1 = 4,00 m, D2 = 2,00 m, D3 = 4,00 m
(Lösung: V3 = 5,00 m3 /s)
Abbildung 4
2
Aufgabe 4: Rotation
1. Die laminare Strömung eines Fluids über eine Platte (vgl. ÜB2 Aufg. 5.1) kann näherungsweise mit
der Gleichung

 

·
u
u(y)
³
´2 ¸
y
U =  v  =  0  ; mit u(y) = umax · 1 − 1 −
; für 0 ≤ y ≤ h
h
w
0
beschrieben werden.
Ist diese Strömung rotationsfrei?
(Lösung: rotationsbehaftet)
2. (Optional) Das Geschwindigkeitsfeld einer Strömung ist in Zylinderkoordinaten (r, ϕ, z) gegeben
durch


¶
µ ³ ´ µ ¶
ur
u
r
r
0
0
U =  uϕ  ; mit uϕ =
· 4·
+
+2
7
r
r0
uz
ur = uz = 0 ;
u0 = const.
a) Stellen Sie die Tangentialgeschwindigkeit uϕ als Funktion des Radius graphisch dar.
b) Aus welchen Anteilen setzt sich die Tangentialgeschwindigkeit zusammen?
c) Genügt die Strömung der Kontinuitätsgleichung?(Begründung)
d) Ist die Strömung rotationsbehaftet?
Hinweis:
Auch in Zylinderkoordinaten kann die Kontinuitätsgleichung durch
∇·U = 0
beschrieben werden, ebenso wie der Drehvektor durch
ω=
1
(∇ × U )
2
.
Hierbei ist nun allerdings


∂/∂r
∇ =  1/r ∂/∂ϕ 
∂/∂z
3

ur
und U =  uϕ 
uz

.