¨Ubung zum Elektronikpraktikum Lösung 1

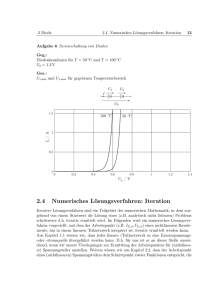
Universität Göttingen
Prof. Dr. Arnulf Quadt
[email protected]
Sommersemester 2010
Raum D1.119
Übung zum Elektronikpraktikum
Lösung 1 - Diode
13. September - 1. Oktober 2010
1. Können die Elektronen innerhalb der erlaubten Bänder des Bändermodells jede
beliebige Energie einnehmen?
Durch die Wechselwirkung, in die die Atome und insbesondere ihre Valenzelektronen
treten, wenn sie sich zu einem Metallkristallverband von N Atomen zusammenfügen,
fächern sich die vorher diskreten Energielinien der freien Atome in Energiebänder
(Größenordnung 1 eV) auf. Diese Bänder bestehen aus N direkt aufeinander folgenden (diskreten!) Energiezuständen. Wegen der großen Zahl N von Atomen, die
ein Metallverband stets enthält, ist die Aufeinanderfolge so dicht, dass man von
einer quasikontinuierlichen Energieniveaufolge sprechen kann, d.h. dass man sagen
kann, dass die Elektronen im Band “frei beweglich” sind, d.h. jede beliebige Energie
innerhalb des Bandes annehmen können.
2. Wie und wann dotiert man Halbleiter? Was sind Donatoren und Akzeptoren?
Bei einem idealen reinen Halbleiter wird die temperaturabhängige Eigenleitfähigkeit
durch die verhältnismäßig geringe Zahl von Elektronen uns sogenannten Löchern
bewirkt, die beim thermischen Aufbrechen einiger Elektronenpaarbindungen der
Halbleiteratome untereinander entstehen.
Abbildung 1: Links: Bändermodell. Rechts: Halbleiter mit Donatoren und Akzeptoren.
Durch gezielte Verunreinigungen kann man diese Leitfähigkeit erhöhen. Diese Vorgang nennt man Dotierung. Bei einer n-Dotierung baut man Fremdatome der 5.
Hauptgruppe in den Halbleiter der 4. Hauptgruppe ein (z.B. Glas oder Si), die zum
Aufbau der Elektronenpaarbildung nur vier Valenzelektronen benötigen, so dass ein
Valenzelektron als negativer Ladungsträger zur Verfügung steht. Fremdatome dieser
Eigenschaft nennt man Donatoren. Ihr Valenzband liegt in der verbotenen Zone des
Halbleiter knapp unter dessen Leitungsband. Somit können Elektronen mit geringerer Energie vom Valenzband des Donators in der Leitungsband des Halbleiters oder
vom Valenzband des Halbleiters in das des Donators springen. Durch die Fremdatome der 3. Hauptgruppe, die nur drei Valenzelektronen in Elektronenpaarbindung
einbringen, entsteht eine Fehlstelle, quasi ein “Loch”, das man anschaulich auch
als positiven Ladungsträger bezeichnen kann. Es ist relativ frei beweglich, denn aus
einer Nachbarbindung wird ein Elektron mit diesem rekombiniert, so dass ein positiver Ladungstransport zum Nachbaratom stattfindet (p-Leitung). Fremdatome dieser
Eigenschaft heien Akzeptoren. Ihr Valenzband liegt ebenfalls oberhalb von dessen
Valenzband. Somit können Elektronen mit geringerer Energie vom Valenzband des
Halbleiters in das des Akzeptors oder von dort in das Leitungsband des Halbleiters
springen.
Durch den Einbau nur eines Fremdatoms pro 108 Atome wird die Leitfähigkeit bei
Zimmertemperatur bereits ca. verzehnfacht.
3. Was bestimmt die Dicke der Grenzschicht bei einem p − n-Halbleiter?
Im Stromlosen Zustand hängt die Dicke der Sperrschicht bei einem pn-Übergang
bei konstanter Temperatur von den Dotierungsstärken nA bzw. nD des p- bzw. nleitenden Materials ab.
Abbildung 2: Links: Sperrschicht eines pn-Übergangs.
Für nA = nD verläuft die Sperrschicht symmetrisch um die Grenzfläche, für unterschiedliche Dotierungsstärken liegt sie um so weiter in dem Gebiet schwächerer
Dotierung. Die Dicke der Schicht ist proportional zu nA und nD , außerdem zur Temperatur. Die Begründung hierfür ist, dass es an der Grenzfläche zur Diffusion von
Elektronen und Defektelektronen zur jeweils anderen Seite kommt, die natürlich von
der stärker dotierten Seite zur schwächer dotierten größer ist als andersherum (vgl.
Osmose).
4. Was sind Donatoren und Akzeptoren? Siehe Frage 1.
Weshalb ist das Kontaktpotential zwischen n- und p-dotiertem Bereich nicht direkt
messbar?
Auch bei Berührung von Messleiter und Halbleiter treten Kontaktspannungen auf,
nämlich gerade zwischen Messleiter und p-dotiertem und Messleiter und n-dotiertem
bereich. Mit einem Messgerät würde man daher nicht die Kontaktspannung zwischen
n- und p-dotiertem Bereich messen, sondern außerdem noch alle anderen auftretenden Kontaktspannungen.
5. Skizzieren Sie den Kennlinienverlauf, I = f (U), folgenmder Zweipole (R = 100 Ω,
D=Typ 1N 4007).
a) Ohmscher Widerstand R. Da R ohmsch ist, gilt I = UR , (R = 100 Ω).
Abbildung 3: Kennlinie eines Ohmschen Widerstandes.
b) Diode in Durchlass bzw. in Sperrichtung. D= Typ 1N4007.
Abbildung 4: Kennlinie einer Diode in Durchlass bzw. in Sperrichtung.
c) Diode und ohmscher Widerstand in Reihe. Es gilt: ID = IR , Uges = UD + UR .
Das zugehörige Kennliniendiagramm ergibt sich durch Äddition in Spannungsrichtung”von a) und b).
Nach Überschreiten der Schwellenspannung ≈ 1 V = US bzw. der Durchbruchsspannung ≈ −1000 V = Ud verliert die Diode in b) praktisch ihren Widerstand und die
Ströme werden sehr groß. Durch R wird dieses in c) verhindert. Für U > US und
U < Ud gilt nämlich U ≈ UR und damit I ≈ UR .
d) Diode und Widerstand aprallel geschaltet. Es gilt: U = UD = UR und Iges =
ID + IR .
Abbildung 5: Kennlinie einer Diode mit ohmschem Widerstand in Reihe.
Abbildung 6: Kennlinie einer Diode mit ohmschem Widerstand parallel.
Für Ud < U < US kann man den Widerstand der Diode als unendlich ansehen
(≫ R). Dann gilt I ≈ IR = UR , d.h. der Graph stellt zwischen UD und US in etwa
eine Gerade I = UR dar. Durch diese Schaltung wird also die Diode für den genannten
Spannungsbereich überbrückt. FüR U < Ud und U > US wird die Diode praktisch
widerstandslos, so dass I ≈ ID wird und nach b) stark anwächst.
6. Wie würden Sie die Schaltung zur Messung der Kennlinie im Durchlassfall aufbauen?
I’
U0
+
D
−
U
R
Abbildung 7: Messung in Durchlassrichtung.
Der Widerstand dient wie in Teil c) der vorherigen Frage besprochen dem Schutz der
Spannungsquelle und der Diode. Ist RU der Innenwiderstand des Spannungsmessers,
so berechnet sich der tatsächlich durch die Diode D fließende Strom als: I = I ′ − RUU .
Aufgrund der Größendordnung des Sperrstromes und des Stromes, der durch das
Voltmeter fließt, wird in Sperrrichtung eine “stromechte” Messung durchgeführt.
7. In der nachfolgend gezeigten Diodenschaltung soll die Ausgangsspannung und der
Strom durch die Diode bestimmt werden.
a) Befindet sich die Diode in Sperr- oder Durchlassrichtung (Begründung geben)?
b) Lösen Sie die Dioden-Kennlinie und berechnen Sie den Strom, der durch die Diode
fließt und die Diodenspannung. Hierbei sein I0 = 2.5 · 10−16 A und die Temperatur
300 K.
c) Nehmen Sie eine idealisierte Diode (feste Diodenspannung) an und bestimmen
wieder den Strom durch die Diode.
hier fehlt noch die Lösung
8. In der nachfolgenden Schaltung wird eine 50 Hz Wechselspannung (12 V) durch
eine (ideale) Diode gleichgerichtet und von dem Kondensator geglättet. Mit der
resultierenden Spannung wird ein Gerät versorgt, welches durch den Widerstand repräsentiert wird. Die Spannung über dem Widerstand darf 8 V nicht unterschreiten.
a) Wie groß muss der Kondensator mindestens dimensioniert werden, um diese Anforderung zu erfüllen?
b) Für welche Zeit pro Periode fließt durch die Diode Strom?
hier fehlt noch die Lösung
D1
1N4001GP
U0
12 V 50 Hz 0 Deg
R1
C1
+
−
100 Ohm
Abbildung 8: Dioden Schaltung.
9. Die folgenden Schaltungen werden mit einer sinusförmigen Eingangsspannung von
U = 3 V Spitze zu Spitze beschaltet. Wie sieht die Ausgansspannung als Funktion
der Zeit aus? Nehmen Sie ideale Dioden an. Die Zener-Dioden sollen eine Zener
Spannung von 2.2 V haben. Stellen Sie das Ausgangssignal graphisch dar.
R1
a)
U0
+
−
D1
D2 UA
R1
b)
U0
+
−
D1
UA
D2
Abbildung 9: Dioden Schaltung.
hier fehlt noch die Lösung
10. Wie groß ist die Ausgangsspannung Ua der folgenden Schaltung? Die Dioden seien
als ideal anzusehen?
hier fehlt noch die Lösung
11. Betrachten Sie folgende Schaltung mit Einweggleichrichtung:
Wie müsste sich die Zeitkonstante τ = R · C zur Schwingungsdauer U∼ verhalten,
um die Welligkeit von U∼ möglichst klein zu halten?
Da D für jede negative Halbwelle von UE sperrt, ergäbe sich ohne die Kapazität
Abbildung 10: Schwingungsdauer bei verschiedenen Kapazitäten C.
C der gestrichelte Verlauf von UA . Zwischen zwei Halbwellen entlädt sich aber der
Kondensator mit der Zeitkonstante τ = RC. Um die Welligkeit von UA möglichst
(Schwingungsdauer von
klein zu halten, sollte τ ≫ T gelten mit T = ν1 = 2π
ω
UE ). Zu groß darf die Kapazität C aber auch nicht gewählt werden, da sonst der
Aufladevorgang des Kondensators zu lange dauert.
12. Berechnen Sie größenordnungsmäßig zu größte Kapazität, die benutzt werden darf,
ohne die Grenzwerte der Diode zu überschreiten. Nehmen Sie dazu an, dass sich
U∼ beim Einschalten um 1 V in 100 µs ändert. Aus dieser Änderung ergibt sich
eine typische Frequenz ν der Fourier-Komponenten der gelieferten Spannung. Die
Grenzwerte häufig verwendeter Dioden sind:
a) Silizium-Diode 1N4007, max. Sperrspannung 1000 V; max. Durchlassstrom
1000 mA
b) Germanium-Diode AA118, max. Sperrspannung 90 V; max. Durchlassstrom
50 mA.
Es gilt: ID = IC + IR > IC = Q̇ = C · U˙A .
Im Durchlassfall fällt an der Diode D die Spannung UD ab, die hier aber zu
1V
vernachlässigen ist. Dann gilt: UA ≈ UE ≈ ∆U
· t mit ∆U
= 100
.
∆t
∆t
µs
ID soll ID,max nicht überschreiten und daher soll IC < ID das schon gar nicht, also
ID,max > IC = C · U˙A = C · ∆U
∆t
ID,max
.
⇒ Cmax = ∆U/∆t
Für D1 (ID1,max = 1 A) und D2 (ID2,max = 50 mA) gilt dann:
Cmax (D1 ) = 100 µF
Cmax (D2 ) = 50 µF
(1)
(2)
13. Welche Belastung erfährt die Diode in der Sperrphase?
Während der positiven Halbwelle von UE∼ wird der Kondensator auf den Maximalwert UA,max = UE,max − UD ≈ UE,max aufgeladen. Ist nun τ = RC so gewählt,
dass die Spannung am Kondensator während der Sperrphase nur wenig abnimmt,
so muss für die Spannung UD,Sperr an der Diode währenddessen gelten, dass sie den
Maximalwert UD,Sperr,max = −UE,max −U1 = −UE,max erreicht, wenn UE,∼ seinen negativen Maximalwert annimmt. Für die Durchbruchsspannung UDb der Diode muss
dann also mindestens gelten: UDb < −UE,max . Strombelastung erfährt die Diode
lediglich durch den Sperrstrom.
14. Skizzieren Sie den zeitlichen Verlauf der Spannung am Ausgang folgendener Schaltungen:
Lösung:
a)
c)
U~
R
U=
b)
U~
R
U=
d)
U~
R
U=
U~
Abbildung 11: Dioden Schaltung zu Aufgabe 14.
U=
Abbildung 12: Spannugsverlauf zu Dioden Schaltung a).
Abbildung 13: Spannugsverlauf zu Dioden Schaltung b).
Abbildung 14: Spannugsverlauf zu Dioden Schaltung c).
Abbildung 15: Spannugsverlauf zu Dioden Schaltung d).
15. Welche Frequenz erwarten Sie für den Restbrumm bei Ein- und Zweiweggleichrichtung?
Bei der Ein- bzw. Zweiweggleichrichtung ändert sich die Ausgangsspannung periodisch mit T bzw. T /2 (T =Periode der Eingangsspannung U∼ ). Für den Restbrumm
der Ausgangsspannung erwartet man daher die einfache bzw. doppelte Frequenz der
Eingangsspannung.
16. * Ein Si pn-Übergang mit einer Querschnittsfläche von 100 µm2 sei mit einer Sperrspannung von 1 V beschaltet. Bestimmen Sie die Kapazität des Übergangs bei
300 K. Hierbei sei NA = 1016 cm−3 (Akzeptoren) und ND = 1015 cm−3 (Donatoren). Wie groß ist die Feldstärke am Übergang?
Hinweis: Bestimmen Sie erstmal die Driftspannung, die sich einstellt und dann die
Dicke der Veramrmungszone. Für Silizium ist ǫ − 11.7.
hier fehlt noch die Lösung