2.4 Numerisches Lösungsverfahren: Iteration

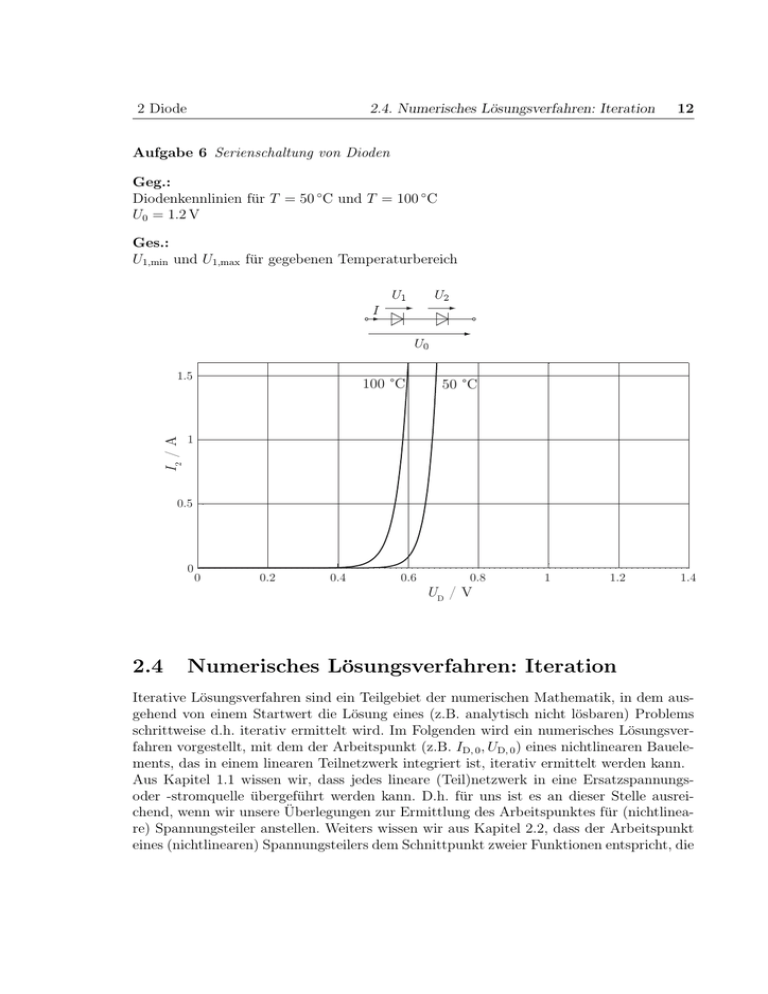
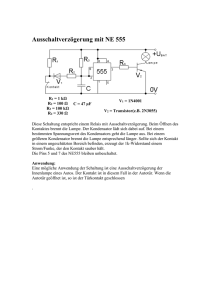
2 Diode
2.4. Numerisches Lösungsverfahren: Iteration
12
Aufgabe 6 Serienschaltung von Dioden
Geg.:
Diodenkennlinien für T = 50 ◦ C und T = 100 ◦ C
U0 = 1.2 V
Ges.:
U1,min und U1,max für gegebenen Temperaturbereich
I2 / A
1.5
100 °C
50 °C
1
0.5
0
2.4
0
0.2
0.4
0.6
0.8
UD / V
1
1.2
1.4
Numerisches Lösungsverfahren: Iteration
Iterative Lösungsverfahren sind ein Teilgebiet der numerischen Mathematik, in dem ausgehend von einem Startwert die Lösung eines (z.B. analytisch nicht lösbaren) Problems
schrittweise d.h. iterativ ermittelt wird. Im Folgenden wird ein numerisches Lösungsverfahren vorgestellt, mit dem der Arbeitspunkt (z.B. ID, 0 , UD, 0 ) eines nichtlinearen Bauelements, das in einem linearen Teilnetzwerk integriert ist, iterativ ermittelt werden kann.
Aus Kapitel 1.1 wissen wir, dass jedes lineare (Teil)netzwerk in eine Ersatzspannungsoder -stromquelle übergeführt werden kann. D.h. für uns ist es an dieser Stelle ausreichend, wenn wir unsere Überlegungen zur Ermittlung des Arbeitspunktes für (nichtlineare) Spannungsteiler anstellen. Weiters wissen wir aus Kapitel 2.2, dass der Arbeitspunkt
eines (nichtlinearen) Spannungsteilers dem Schnittpunkt zweier Funktionen entspricht, die
2 Diode
2.4. Numerisches Lösungsverfahren: Iteration
13
den Spannungsteiler vollständig beschreiben. (Zwei passive Bauelemente → zwei Funktionen).
Beim Iterationsverfahren für (nichtlineare) Spannungsteiler wird nun ausgehend von einem
(erratenem) Startwert U2, 0 der Strom I2, 0 berechnet, mit dem in den folgenden Iterationsschritten wiederum die Spannung U2, 1 und folglich der Strom I2, 1 etc. berechnet werden.
Die Konvergenz hängt in diesen Fällen nicht von der Wahl des Startwertes sondern nur
von der Iterrationsrichtung ab.
Für den Spannungsteiler ergeben sich zwei mögliche Iterationsmöglichkeiten, die wir anhand eines linearen Spannungsteilers erläutern möchten, wobei um die Analogie mit einem
nichtlinearem Spannungsteiler herzustellen R1 >> R2 vorausgesetzt wird. Eine ausführlichere Beschreibung des Iteartionsverfahrens ist im Anhang A zu finden.
1. Möglichkeit
divergiert
2. Möglichkeit
konvergiert
Fazit: Die Spannungen müssen in die flachere Kennlinie eingesetzt werden.
2 Diode
2.5. Kleinsignalverhalten
14
Aufgabe 7 Iterartion
Geg.:
U0 = 15 V
R1 = 25 Ω
IS = 1 · 10−12 A
n=1
T = 25 ◦ C
0.7
0.7
0.6
0.6
0.5
0.5
0.4
0.4
0.3
0.3
0.2
0.2
0.1
0.1
0
2.5
ID / A
ID / A
Wenden Sie die zwei Möglichkeiten der Iteration an um den AP zu finden und erläutern
Sie die beiden Vorgangsweisen grafisch.
0
0.2
0.4
0.6
0.8
UD / V
1
1.2
0
0
0.2
0.4
0.6
0.8
UD / V
1
1.2
Kleinsignalverhalten
Im Folgenden betrachten wir den Fall, dass der Spannungsquelle des nichtlinearen Spannungsteilers eine Wechselspannung überlagert ist; siehe Abb. 2.4. Für den Fall, dass diese
überlagerte Wechselspannung klein gegenüber der Gleichspannung UB ist (daher auch der
Name Kleinsignal) wirkt die Diode für diese Wechselgröße wie ein lineares Bauelement
d.h. wie ein Ohmscher Widerstand. Die Größe dieses Widerstandes ist vom AP der Diode
abhängig und entspricht dem Kehrwert der Tangente der Diodenkennlinie im AP.
�
0
1
dID ��
IS UnD,
ID, 0
=
=
e UT ≈
(2.4)
�
rD
dUD AP n UT
n UT
rD ≈
n UT
ID, 0
(2.5)
2 Diode
2.5. Kleinsignalverhalten
Schaltung mit
Wechselspannungsquelle
1. Großsignalbetrachtung
Ermittlung des AP
2. Kleinsignalbetrachtung
Schwankungen um AP
Abbildung 2.4: Kleinsignalbetrachtung
Aufgabe 8 Kleinsignalbetrieb
Geg.:
UD, 0 = 625.31 mV
ID, 0 = 37.47 mA
UB = 1 V, Û = 0.25 V
R1 = 10 Ω
IS = 1 · 10−12 A
n=1
T=25 ◦ C
Ges.:
Minimale und maximale Diodenspannung
a) grafisch
b) mit Kleinsignalbetrachtung
0.1
0.08
ID / A
0.06
0.04
0.02
0
0
0.2
0.4
0.6
UD / V
15
0.8
1
1.2
2 Diode
2.5. Kleinsignalverhalten
16
0.1
0.08
ID / A
0.06
0.04
0.02
0
0
0.2
0.4
0.6
UD / V
0.8
1
1.2
Aufgabe 9 Kleinsignal-Abschwächer
Die gegebene Schaltung kann dazu verwendet werden um kleine Wechselspannungen zu
dämpfen, wobei der Dämpfungsgrad mit dem Potentiometer RV variiert werden kann.
RV
R1
500O
Ω
C
ue
UB
10V
C
D
ua
a) Zeichnen Sie das Gleichstromersatzschaltbild und zeigen Sie die Funktion des
Abschwächers grafisch. Zeichnen Sie zwei Potistellungen ein und kennzeichnen Sie
die stärkere Abschwächung. Geben Sie den Diodenstrom unter der Annahme, dass
UD in der Gleichstrom-Analyse konstant mit 0.6V angenommen werden kann, an.
b) Geben Sie den differenziellen Widerstand der Diode D in Abhängigkeit vom Diodenstrom ID an.
2 Diode
2.6. Zenerdiode
17
c) Zeichnen Sie das (linearisierte) Kleinsignalersatzschaltbild des Abschwächers.
Die Kondensatoren können für die Wechselstrombetrachtung durch Kurzschlüsse
ersetzt werden, da die Werte für C sehr groß seien.
d) Das Verhältnis von ua /ue = k ist mit dem Potentiometer RV einstellbar. Geben Sie
aus dem Kleinsignalersatzschaltbild eine Beziehung für den dazu nötigen differenziellen Diodenwiderstand rD sowie für den zugehörigen Diodenstrom ID an.
e) Berechnen Sie (aus a) und d)) die Widerstandswerte RV,max und RV,min um eine
Abschwächung im Bereich k = 1/3 . . . 1/100 zu erreichen.
f) Berechnen Sie ID,min und ID,max
Hinweise:
zu a) Alle transienten Vorgänge sind angeklungen!
UD
zu b) und d) Benutzen Sie als Diodengleichung ID ≈ IS e mUT mit m = 2 und UT = 25mV.
2.6
Zenerdiode
Aufgabe 10 Spannungsstabilisierung mit Zenerdioden
Zener-Dioden sind Dioden mit definiertem Durchbruchverhalten in Sperrrichtung vergleichsweise niederohmig. Sie können aufgrund des steilen Kennlinienverlaufes im Durchbruch zur Spannungsstabilisierung verwendet werden. Die folgende Schaltung zeigt eine
dafür geeignete Schaltung bestehend aus einer Zenerdiode, einem Vorwiderstand und einer
variablen Last. Die Schaltung soll für die folgenden Spezifikationen ausgelegt werden:
R
U
IZ
IL
UZ
RL
Eingangsspannung:
schwankt zwischen den Werten Umin = 10V und Umin = 15V
Diode:
Zenerspannung:
maximale Verlustleistung:
minimaler Strom durch die Zener-Diode:
UZ,Nenn = 8.2V
PV,max = 0.2W
IZ,min = 1mA
Ua
2 Diode
2.6. Zenerdiode
18
Last:
minimale Belastung
maximale Belastung
IL,min = 0 mA (Leerlauf)
IL,max = 4 mA
Für a) und b) wird im Folgenden angenommen, dass UZ ≈ UZ, Nenn (warum ist diese
Annahme gerechtfertigt?)
a) Berechnen Sie anhand der vorgegebene Daten der Zener-Diode den maximal erlaubten Strom. Warum sollte auch der minimale Strom nicht unterschritten werden?
b) Da der Strom durch die Zener-Diode in dem Bereich zwischen und liegen sollte,
ergibt sich auch ein minimaler und ein maximaler Vorwiderstand. Berechnen Sie
diesen Widerstandsbereich und wählen Sie einen geeigneten Vorwiderstand aus der
E24-Normreihe aus:
1.0 / 1.1 / 1.2 / 1.3 / 1.5 / 1.6 / 1.8 / 2.0 / 2.2 / 2.4 / 2.7 / 3.0 / 3.3 / 3.6 / 3.9 /
4.3 / 4.7 / 5.1 / 5.6 / 6.2 / 6.8 / 7.5 / 8.2 / 9.1
Die Zener-Diode kann etwas genauer durch ein Ersatzschaltbild modelliert werden (gilt
solange die Spannung an der Z-Diode > UZ, Nenn ist! Gilt nicht für Dioden in Vorwärtsrichtung! )
UZ
r Z= 4Ω
Ersatzschaltung
c) Ein Maß für die Güte der Stabilisierungsschaltung ist der Stabilisierungsfaktor S,
welcher das Verhältnis der relativen Spannungsänderung am Eingang der Schaltung
zur relativen Spannungsänderung am Ausgang der Schaltung angibt. Berechnen Sie
mit Hilfe der Kleinsignalersatzschaltung der Zener-Diode die Aussgangsspannungsschwankung ∆Ua sowie den Stabilisierungsfaktor für Leerlauf und Volllast (berechnen Sie dazu RL unter der Annahme UZ ≈ UZ, Nenn ).
d) Berechnen Sie mit Hilfe der Großsignalersatzschaltung eine Beziehung, die die Ausgangsspannung in Abhängigkeit der Eingangsspannung angibt. Verwenden Sie dazu
den Überlagerungssatz.
2 Diode
2.7
2.7. Weiterführende Aufgaben
19
Weiterführende Aufgaben
Aufgabe 11 Diodenschaltung
Geg.:
UB = 5 V, Û = 0.5 V
R1 = 100 Ω, R2 = 25 Ω, R3 = 5 Ω
IS = 5.78 · 10−12 A
n = 1.2
UT = 25 mV
Ges.:
a) Ermitteln Sie den Arbeitspunkt sowohl grafisch als auch numerisch
b) Bestimmen Sie die minimale und maximale Ausgangsspannung sowohl grafisch als
auch rechnerisch (Kleinsignalbetrachtung)
c) Bestimmen Sie den Ausgangswiderstand der Schaltung ra =
d Ua
d Ia
2 Diode
2.7. Weiterführende Aufgaben
0.35
0.3
ID / A
0.25
0.2
0.15
0.1
0.05
0
0
0.2
0.4
0.6
UD / V
0.8
1
1.2
20