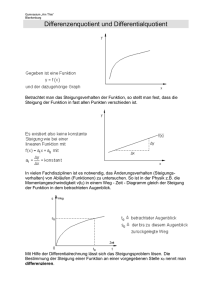
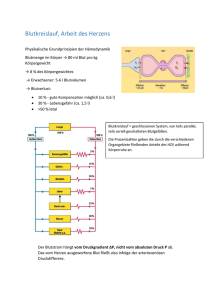
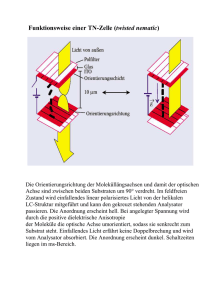
1 Grundlagen der Volkswirtschaftslehre: Mathematik und grafische

15
1 Grundlagen der Volkswirtschaftslehre:
Mathematik und grafische Darstellungen
In diesem Kapitel…
▪ Volkswirtschaft und Volkswirtschaftliche Modelle
▪ Werkzeugkasten aus der Mathematik
▪ Richtiges Darstellen
Die Ökonomik, die Wirtschaftswissenschaften oder die Volkswirtschaftslehre
untersuchen das Verhalten der Wirtschaft – sowohl das Verhalten Einzelner
(Privatpersonen, Unternehmen) als Teil der Wirtschaft als auch der Wirtschaft als Ganzes. Dieses Buch stellt die Sprache der Volkswirtschaftslehre in
den Vordergrund. Es ist als Ergänzung zu einem Standardlehrbuch gedacht.
Das Hauptaugenmerk dieses Kapitels liegt auf den mathematischen Grundlagen, die man in der Volkswirtschaftslehre verwendet.
Einführung in die Volkswirtschaftslehre
Die Volkswirtschaftslehre wird in Mikroökonomik und Makroökonomik eingeteilt. Die Mikroökonomik befasst sich mit Fragen zum Verhalten Einzelner: einzelner Personen oder Haushalte, einzelner Unternehmen, einzelner
Märkte. Fragen der Mikroökonomik sind zum Beispiel:
▪ Was bestimmt den Preis eines Produkts?
▪ Wie groß ist die Produktionsmenge eines Unternehmens?
▪ Was bestimmt die Löhne oder das Lohniveau auf dem Arbeitsmarkt?
Die Makroökonomik befasst sich mit Fragen zu dem Verhalten von Gruppen, mit der Wirtschaft als Ganzes. Volkswirte benutzen manchmal das Wort
aggregieren oder Aggregat (Gesamtgröße), um solche Gruppen zu beschreiben. Makroökonomik bezieht sich normalerweise auf die Wirtschaft eines
Landes, zum Beispiel die US-amerikanische Wirtschaft. Aber die Grundlagen
der Makroökonomik können auf jede Gesamtwirtschaft angewendet werden:
eine Region, einen Staat, einen Bezirk, eine Stadt. Fragen der Makroökonomik sind zum Beispiel:
16
1 Grundlagen der Volkswirtschaftslehre: Mathematik und grafische Darstellungen
▪ Was bestimmt die Inflationsrate in einer Volkswirtschaft?
▪ Was bestimmt die Arbeitslosenquote in einer Volkswirtschaft?
▪ Was bestimmt das Gesamteinkommen einer Volkswirtschaft?
Volkswirtschaftliche Analysen – egal ob es sich um Mikroökonomik oder Makroökonomik handelt – können in zwei Kategorien unterteilt werden: positive Ökonomik und normative Ökonomik. Positive Ökonomik beantwortet
Fragen, die normalerweise als „Wie beeinflusst dieser Faktor jenes Ergebnis?“ formuliert werden: Wie wirkt sich ein Anstieg des Einkommens auf den
Preis von Flugtickets aus? Wie wirkt sich ein Rückgang des Konsums der privaten Haushalte auf die Zahl der Arbeitsplätze in einer Wirtschaft aus? Normative Ökonomik beantwortet Fragen, die normalerweise als „Soll diese
Maßnahme ergriffen werden?“ formuliert sind: soll der Stadtrat eine Mietpreisbremse einführen? Soll die Bundesregierung die Steuern erhöhen?
Meistens ist die volkswirtschaftliche Analyse positive Ökonomik. Die positive
Ökonomik umfasst die Analyse einer Frage, jedoch nicht ein Urteil darüber,
was für eine Gesellschaft am besten wäre. Normative Ökonomik beinhaltet
ein Werturteil. Wenn wir eine normative Analyse vornehmen – soll diese
Maßnahme ergriffen werden – ist es notwendig, die Ziele, die wir erreichen
wollen, festzulegen. Volkswirte, die unterschiedlicher Meinung sind, können
sich in der Regel auf die positive Analyse einigen: Wie wird sich diese Politik
auf die Wirtschaft auswirken? Aber sie sind unterschiedlicher Meinung, was
das gewünschte Ziel ist: Ist es unser Ziel, Ungleichheiten abzubauen oder
das Wachstum zu fördern? Geht es darum, die Inflation zu verringern oder
Arbeitsplätze zu schaffen? Wenn man Volkswirte streiten hört, sind sie meist
uneins über die gesellschaftlichen Ziele, die sie verfolgen.
Die Verwendung empirischer Belege ist ebenfalls ein wichtiger Teil der
Volkswirtschaftslehre. Empirische Belege, das heißt Daten – Statistiken, Zahlen – können dazu verwendet werden, Argumente zu stützen. Um wie viel
ändern sich die Ausgaben für Ravioli in Dosen, wenn Familien weniger Geld
zur Verfügung haben? „Um wie viel“ ist eine empirische Frage, eine Frage,
die eine numerische (empirische) Antwort verlangt.
Die Volkswirtschaftslehre ist zudem eine Sozialwissenschaft, die mathematische Hilfsmittel verwendet. Sie ist eine Sozialwissenschaft, da sie sich mit
dem Verhalten von Menschen befasst. Sie verwendet Grundlagen der Mathematik, da Ideen, Theorien, Modelle und empirische Belege zum wirtschaftlichen Verhalten der Menschen mathematisch ausgedrückt werden.
Volkswirtschaftliche Modelle
17
Volkswirtschaftliche Modelle
Volkswirtschaftliche Modelle werden in der Volkswirtschaftslehre zur
Beantwortung von Fragen verwendet. Es handelt sich dabei fast nie um physikalische Modelle, wie zum Beispiel Modellflugzeuge. Vielmehr sind volkswirtschaftliche Modelle eine formelhafte Art und Weise, wie Wirtschaftswissenschaftler Fragen stellen und Geschichten erzählen. Volkswirtschaftliche
Modelle sind die Geschichten, die wir erzählen.
Jedes volkswirtschaftliche Modell besteht aus drei Elementen:
1. Einer Frage
2. Vereinfachungen und Abstraktionen der wirklichen Welt
3. Annahmen über wirtschaftliches Verhalten
Wenn man einen dieser drei Aspekte verändert, erhält man ein anderes Modell.
Lautet die Frage zum Beispiel: „Was bestimmt den Preis einer Essiggurke?“,
ist das passende Modell das von Angebot und Nachfrage (Kapitel 3). Aber
wenn die Frage stattdessen lautet: „Was bestimmt die Arbeitslosenquote?“,
verwenden wir ein anderes Modell. Sobald die Fragestellung verändert wird,
passt ein anderes Modell, eine andere volkswirtschaftliche Geschichte.
Eine Vereinfachung der komplexen Welt, in der wir leben, besteht darin, sie
in vier Gruppen einzuteilen: private Haushalte, Unternehmen, Staat und den
Rest der Welt. Wenn wir diese Vereinfachung vornehmen, verwenden wir ein
makroökonomisches Modell, das Modell nach Keynes oder auch den Keynesianismus (dies wird im Begleitband Wiley-Schnellkurs Makroökonomie abgedeckt). Aber wenn stattdessen die Welt in nur zwei Gruppen eingeteilt
wird – Kapitalisten und Arbeitskräfte – verwenden wir ein anderes Modell.
Sobald die Vereinfachung verändert wird, passt ein anderes Modell, eine andere volkswirtschaftliche Geschichte.
Wenn wir zum Beispiel annehmen, dass Haushalte ihre jährlichen Ausgaben
auf Grund der Überlegung festlegen, wie viel sie sparen müssen, um nach
Ende ihres Arbeitslebens ein gutes Auskommen zu haben, verwenden wir
das sogenannte Lebenszyklus-Modell. Aber wenn wir stattdessen annehmen,
dass Haushalte ihre jährlichen Ausgaben aufgrund der Überlegung festlegen,
wie viel Einkommen im laufenden Jahr zur Verfügung steht, verwenden wir
wieder ein anderes Modell. Sobald die Annahme verändert wird, passt ein
anderes Modell, eine andere volkswirtschaftliche Geschichte.
Volkswirtschaftliche Modelle werden auf drei verschiedene Arten dargestellt:
18
1 Grundlagen der Volkswirtschaftslehre: Mathematik und grafische Darstellungen
▪ Mithilfe von Worten
▪ Mithilfe von mathematischen Gleichungen
▪ Mithilfe grafischer Darstellungen
Die meisten Modelle werden auf zwei Arten dargestellt (mit Worten und
einer anderen); manche werden auch auf alle drei Arten dargestellt.
Wenn Sie die Worte nicht verstehen, sehen Sie sich die grafische Darstellung
an. Wenn eine Grafik keinen Sinn ergibt, sehen Sie sich die Gleichung oder
die Worte an. Die drei Arten, ein Modell darzustellen, ergänzen und unterstützen einander. Stellen Sie sich diese Arten als drei Sprachen vor, die alle
das Gleiche sagen. Letztendlich sollten Sie in der Lage sein, alle drei Darstellungsarten eines jeden Modells zu verstehen und mühelos zwischen ihnen
wechseln können.
Mathematische Grundlagen
In einem Kurs zu den Grundlagen der Volkswirtschaftslehre müssen Sie
auch einige Grundlagen der Mathematik anwenden können. Wir besprechen
hier die am häufigsten verwendeten mathematischen Hilfsmittel. Die grafische Darstellung (die im nächsten Abschnitt besprochen wird) ist sehr
wichtig, um das Studium der Volkswirtschaft erfolgreich zu absolvieren.
Schauen Sie immer wieder in diesem Kapitel nach, solange Sie noch nicht
ganz sicher in der Anwendung dieser Grundlagen sind.
Brüche und Dezimalzahlen
In einigen Teilbereichen der Volkswirtschaftslehre verwenden wir Brüche, in
anderen Dezimalzahlen. Sie sollten mühelos zwischen Brüchen und Dezimalzahlen wechseln können. Außerdem sollten Sie ohne weiteres Brüche
kürzen können. Beispiele:
▪
30 3
¼ ¼ 0;75
40 4
▪
20 1
¼ ¼ 0;5
40 2
▪ 0;6 ¼
6
;
10
also
1
10 5
¼
¼
0;6
6
3
Mathematische Grundlagen
19
Absoluter Wert
In manchen Fällen benutzt man in der Volkswirtschaftslehre absolute Werte.
Der absolute Wert einer Zahl ist der Abstand dieser Zahl von Null (unabhängig
davon, ob die Zahl über oder unter Null liegt). Der absolute Wert einer Zahl
wird durch zwei gerade Linien gekennzeichnet: | |. Also |4| = 4 und |–4| = 4.
Darstellung als Funktion
Vieles wird in der Volkswirtschaftslehre in Gleichungen ausgedrückt und
durch Symbole abgekürzt. Zum Beispiel schreibt ein Volkswirt den einfachen
Satz „Wie viel Limonade jemand kaufen will, hängt vor allem vom Preis der
Limonade ab“ als xN = f(p). Volkswirte bezeichnen diese Art, eine Beziehung
in einer Gleichung darzustellen, als Funktion. Es ist wichtig, diese Gleichungen „lesen“ zu können.
Welche Worte kommen Ihnen in den Sinn, wenn Sie „xN = f(p)“ lesen? Wenn
Sie „x tiefgestellt N ist gleich f Klammer auf p Klammer zu“ gedacht haben,
werden Sie in der Volkswirtschaftslehre eine Menge Probleme bekommen.
Ihre Voraussetzungen sind besser, wenn Sie diese Gleichung als „x von N ist
gleich eine Funktion von p“. gelesen haben. Aber um die Volkswirtschaftslehre wirklich verstehen zu können, müssen Sie „xN = f(p)“ als „die nachgefragte Menge hängt vom Preis ab“ lesen können.
Es hängt von zwei Dingen ab, ob Sie Gleichungen erfolgreiche lesen können;
Sie müssen:
▪ In der Lage sein, die Funktion, wie zum Beispiel f( ) in Worte übersetzen
zu können,
▪ Wissen, für was die Symbole stehen.
Um zu wissen, für was xN, p und weitere Symbole stehen, müssen Sie sich
ihre Bedeutung einprägen. Es wird leichter, sich an die Symbole und Notationen (d. h. Schreibweisen) zu erinnern, wenn Sie immer die gleichen verwenden. Stellen Sie sich das wie Twittern für die Volkswirtschaftslehre vor.
Tipp
Beginnen Sie, indem Sie eine Liste der Notationen aus Ihrem Buch anlegen. Jedes Mal, wenn
der Dozent „Preis“ sagt, schreiben Sie „p“ auf. Wenn er oder sie „Menge“ sagt, schreiben Sie
„x“ und so weiter.
20
1 Grundlagen der Volkswirtschaftslehre: Mathematik und grafische Darstellungen
Variablen
In der Volkswirtschaftslehre wird ständig den Begriff „Variable“ benutzt. Dies
ist eines der vielen Beispiele, wie ein allgemein gebräuchliches Wort in der
Sprache der Ökonomik eine andere, fachsprachlichere Bedeutung hat als in
der Alltagssprache. Eine Variable ist etwas, dessen Wert sich verändern
kann. Der Preis einer Packung Taschentücher im Supermarkt um die Ecke
war vielleicht in den letzten vier Monaten derselbe, aber Volkswirte sagen,
dass der Preis eine Variable ist, da sich der Wert ändern kann. Die Variable
ist der „Preis“, die Notation, die wir für dieseVariable verwenden ist p.
Es gibt zwei Arten von Variablen: abhängige und unabhängige. Der Wert
einer abhängigen Variablen hängt von dem Wert der unabhängigen Variablen ab. Wie viel eine Familie monatlich ausgibt, hängt von ihrem Einkommen ab. Die „Ausgaben einer Familie“ ist eine abhängige Variable, deren
Wert von der unabhängigen Variablen „Familieneinkommen“ bestimmt
wird. Die Ausgaben und das Einkommen einer Familie sind beides Variablen, da die Werte von beiden sich verändern können. In jeder Beziehung
gibt es nur eine abhängige Variable, aber keine Einschränkung wie viele unabhängige Variablen es geben kann.
Algebra
In der Makroökonomik löst man oft algebraische Gleichungen mit einer Unbekannten. Was ist zum Beispiel der Wert von Y, wenn
Y = 100 + 0,6 Y
Um diese Gleichung zu lösen, stellen Sie die Gleichung um. (Zur Erinnerung:
Y ist gleich 1 × Y)
Y – 0,6 Y = 100
0,4 Y = 100
und dann teilen Sie beide Seiten der Gleichung, um Y zu isolieren.
0; 4Y 100
¼
0; 4
0; 4
Y = 250
Grafische Darstellungen
21
Δ bedeutet „Veränderung“
In der Volkswirtschaftslehre werden wir immer wieder von der Veränderung
des Werts einer Variablen sprechen. Man verwendet den griechischen Großbuchstaben Delta Δ, um eine Veränderung auszudrücken. Demnach wird Δx
als „eine Veränderung von x“ gelesen. ΔY ist „die Veränderung von Y“. „Veränderung von“ mit Δ zu ersetzen, ist eine weitere Abkürzung, die Sie ab jetzt
verwenden sollten, wenn Sie sich Notizen im Kurs machen.
Die Berechnung des Grads einer Veränderung
In manchen Fällen muss man den Grad der Veränderung einer Variablen
zwischen zwei Werten berechnen, das heißt die prozentuale Veränderung.
Wenn sich Q zum Beispiel von 50 auf 60 erhöht, um welchen Prozentsatz hat
sich Q erhöht?
Die allgemeine Formel zur Berechnung des Prozentsatzes der Veränderung ist
ðneuer Wert " alter WertÞ
alter Wert
Wenn Q von 50 auf 60 steigt, beträgt der Prozentsatz der Veränderung (60 –
50)/50 = 10/50 = 0,2 oder 20 Prozent.
Aufgaben
Versuchen Sie, folgende Rechenaufgaben zu lösen.
Die Antworten für alle Aufgaben finden Sie am Ende des Buches.
1.1
Um wie viel Prozent verändert sich das Einkommen, wenn das Einkommen
von 100 auf 110 steigt?
1.2
Um wie viel Prozent verändert sich das Einkommen, wenn das Einkommen
von 110 auf 100 sinkt?
Grafische Darstellungen
Beim Durchblättern von VWL-Büchern werden Sie viele Diagramme und
Kurven sehen. Für das Studium der Volkswirtschaftslehre ist es wichtig, Kurven zeichnen, interpretieren und analysieren zu können.
22
1 Grundlagen der Volkswirtschaftslehre: Mathematik und grafische Darstellungen
Die Grundlagen
Fast alle grafischen Darstellungen in der Volkswirtschaftslehre sind zweidimensionale Diagramme – ein Koordinatensystem, in dem dargestellt wird,
was mit zwei Variablen geschieht. Ein zweidimensionales Diagramm hat
eine waagrechte und eine senkrechte Achse. Der Punkt, in dem sich die
zwei Achsen schneiden, wird als Nullpunkt (Ursprung) bezeichnet. Die Werte, die auf der waagrechten Achse dargestellt werden, können negative Werte
links des Nullpunkts oder positive Werte rechts des Nullpunkts sein. Die
Werte, die auf der senkrechten Achse dargestellt werden, können negative
Werte unterhalb des Nullpunkts oder positive Werte oberhalb des Nullpunkts
sein.
Jeder Punkt in einem Koordinatensystem hat gleichzeitig die Werte beider
Variablen. Zur Veranschaulichung hier ein Beispiel: Der Wert der Variable d
wird auf der senkrechten Achse abgetragen, und der Wert der Variable w
wird auf der waagrechten Achse angetragen. Punkt A in Abb. 1.1 beschreibt
einen negativen Wert von w (er liegt links vom Nullpunkt) und einen negativen Wert von d (er liegt unterhalb des Nullpunkts). Punkt B beschreibt einen
positiven Wert von w (er liegt rechts vom Nullpunkt) und einen negativen
Wert von d (er liegt unterhalb des Nullpunkts).
d
positive Werte von d
Nullpunkt 0
negative Werte von w
A
Bei A, w < 0 und d < 0
positive Werte von w
w
B
Bei B, w > 0 und d < 0
negative Werte von d
Abbildung 1.1 Eine zweidimensionale grafische Darstellung im Koordinatensystem.
Grafische Darstellungen
23
senkrechte
Achse
Nullpunkt oder 0
waagerechte Achse
Abbildung 1.2 Der 1. Quadrant, oben rechts.
Zweidimensionale grafische Darstellungen zeigen, was mit zwei Variablen
geschieht. Die waagrechte Achse und senkrechte Achse kreuzen sich am
Nullpunkt. Jeder Punkt im Koordinatensystem hat gleichzeitig zwei Werte.
Punkt A beschreibt einen negativen Wert von w (w < 0) und einen negativen
Wert von d (d < 0).
Die Achsen teilen das Diagramm in vier Bereiche, die Quadranten genannt
werden. Da die meisten Variablen in der Volkswirtschaftslehre nur positive
Werte annehmen, verwendet man fast immer nur den 1. Quadranten, der
sich oben rechts befindet. Deshalb sehen die meisten grafischen Darstellungen in Koordinatensystemen wie in Abb. 1.2 aus.
Da die meisten Variablen, die in der Volkswirtschaftslehre gemessen werden, nur
positive Werte annehmen, verwendet man bei der grafischen Darstellung nur
den oberen, rechten Quadranten eines zweidimensionalen Koordinatensystems.
In Anlehnung an den Mathematikunterricht in der Schule nennen manche
Bücher die waagrechte Achse (Abszisse) die „x-Achse“ und die senkrechte
Achse (Ordinate) die „y-Achse“. Seien Sie jedoch mit der Verwendung dieser
Terminologie vorsichtig. Es gibt ökonomische Variablen die mit x bezeichnet
werden (zum Beispiel Mengen) und y (normalerweise das Einkommen), aber
sie werden nicht immer auf der entsprechenden x- oder y-Achse abgetragen.
Wenn Sie „waagrechte Achse“ und „senkrechte Achse“ schreiben, vermeiden
Sie Verwechslungen.
24
1 Grundlagen der Volkswirtschaftslehre: Mathematik und grafische Darstellungen
Darstellung von Daten
Wenn wir Informationen (Daten) von zwei Variablen haben, können wir die
Daten in ein Diagramm eintragen. Angenommen, wir haben Informationen
über das durchschnittliche Einkommen, das Menschen im Jahr 2003 verdient
haben, geordnet nach Ausbildungsjahren. Man kann nun die Information in
einem (umständlichen!) Satz ausdrücken: 2003 verdienten Menschen mit
einem Highschool-Abschluss im Durchschnitt 28.000 $ im Jahr. Menschen
mit einem Collegeabschluss verdienten 51.000 $, und diejenigen mit einem
Masterabschluss verdienten 62.000 $.
Oder man stellt die Informationen in einer Tabelle, also tabellarisch, dar:
Ausbildungsgrad
Jahre der Ausbildung
Durchschnittliches Einkommen 2003
High School Diploma
12
28.000 $
College Diploma
16
51.000 $
Master
18
62.000 $
Tabelle 1.1 Das Einkommen steigt mit der Ausbildung.
Quelle: U.S. Census Bureau, Statistical Abstract of the United States: 2006 , Tabelle 217.
Es ist mit Sicherheit leichter, aus der Tabelle als aus dem Satz herauszulesen,
dass ein höherer Abschluss höheres Einkommen bedeutet. Wie sieht die Darstellung in einem Diagramm aus?
Um die Daten einzuzeichnen, tragen Sie eine Variable an der waagrechte
Achse und die andere Variable an der senkrechte Achse ab. Oft – aber nicht
immer – wird in der Volkswirtschaft die unabhängige Variable auf der waagrechte Achse abgetragen und die abhängige Variable auf der senkrechten.
Die unabhängigen Variablen sind diejenigen, die den Wert der abhängigen
Variablen bestimmen.
Jeder Punkt im Koordinatensystem in Abb. 1.3 steht für einen Kombination
zweier Werte. Punkt A zeigt, dass das durchschnittliche Einkommen von
Menschen mit 12jähriger Ausbildung (auf der waagrechten Achse abgetragen) 28.000 $ (auf der senkrechten Achse abgetragen) beträgt. Punkt C zeigt,
dass diejenigen mit 18 Jahren Ausbildung ein durchschnittliches Jahreseinkommen von 62.000 $ erhalten.
Grafische Darstellungen
25
Abgeschnittene Achsen
Beachten Sie, dass die Achsen in unserem Koordinatensystem abgeschnitten
sind. Eine abgeschnittene Achse lässt Werte zwischen 0 und einem anderen
Wert aus. Die zwei Zeichen // neben dem Nullpunkt kennzeichnen diese
Auslassung. Die waagrechte Achse ist zwischen 0 und 12 Jahren abgeschnitten. Die senkrechte Achse ist zwischen 0 € und 20.000 € abgeschnitten.
Kurven
Manchmal wird ein Verhältnis mithilfe einer Kurve statt durch einzelne
Punkte dargestellt. Die Kurve – eine ununterbrochene Linie die sowohl gerade als auch nicht gerade sein kann – verbindet tatsächliche Daten. In
Abb. 1.4 werden die Daten aus der Abb. 1.3 durch eine Kurve verbunden.
Jeder Punkt in dem Koordinatensystem steht für eine Kombination aus zwei
Werten. Das jährliche Einkommen wird auf der senkrechten Achse abgetragen. Die Jahre der Ausbildung werden auf der waagrechten Achse abgetragen. Punkt A zeigt, dass die Menschen mit 12 Jahren Ausbildung ein durchschnittliches Jahreseinkommen von 28.000 $ verdienten.
Jährliches
Einkommen
(in €)
60.000
C
B
50.000
40.000
30.000
A
20.000
12
14
Abbildung 1.3 Punktuelle Darstellung von Daten.
16
18
20 Ausbildungsjahre
26
1 Grundlagen der Volkswirtschaftslehre: Mathematik und grafische Darstellungen
Jährliches
Einkommen
(in €)
60.000
C
B
50.000
40.000
30.000
A
20.000
12
14
16
18
20 Ausbildungsjahre
Abbildung 1.4 Verbindung der einzelnen Datenpunkte zu einer Kurve.
Ein Verhältnis zweier Variablen zueinander kann durch eine Kurve dargestellt werden, die einzelne Datenpunkte verbindet. Ausgehend von den
Daten in Tabelle 1.1 zeigt die Kurve, dass das durchschnittliche Jahreseinkommen mit der Anzahl der Ausbildungsjahre steigt.
In der Volkswirtschaftslehre zeichnen wir oft Kurven ohne die Zahlenwerte
der beiden Variablen anzugeben. Wenn wir wissen, dass reichere Haushalte
mehr als ärmere Haushalte ausgeben oder konsumieren, können wir dieses
Verhältnis als Kurve darstellen. Diese Kurve zeigt, dass der Konsum steigt,
wenn das Vermögen steigt. Der Konsum wächst jedoch weniger, wenn das
Vermögen stark zugenommen und eine gewisse Höhe erreicht haben.
Die Kurve kann ein Verhältnis ohne tatsächliche Daten darstellen. Abb. 1.5
zeigt, dass der Konsum von Haushalten höher ist, wenn die Haushalte über
mehr Vermögen verfügen. Punkt A in der Abb. 1.5 bezeichnet zum Beispiel
bestimmte Werte von Konsum und Vermögen. Wenn man eine rechtwinklige
Linie von Punkt A zur senkrechten Achse zieht, findet man den Wert des
Konsums, eine Linie zur waagrechten Achse zeigt den Wert der Vermögens.
Punkt A bezeichnet die Kombination aus der Höhe des Vermögens A1 und
der Höhe des Konsums A2. Punkt B bezeichnet die Kombination aus der
Höhe der Vermögens B1 und der Höhe des Konsums B2.
Grafische Darstellungen
27
Konsum
B
B2
A2
A
A1
B1
verfügbare
Geldmittel
Abbildung 1.5 Kurve ohne Zahlen.
Grafische Darstellungen lesen
Es ist genauso wichtig, grafische Darstellungen „lesen“ zu können wie Gleichungen lesen zu können. Wenn Sie Abb. 1.5 ansehen, welche Wörter (wenn
überhaupt!) gehen Ihnen durch den Kopf? Eine Möglichkeit ist: „Ein Diagramm mit dem Konsum auf der senkrechten und dem Vermögen auf der
waagrechten Achse zeigt eine Kurve mit einer Steigung.“ Das ist richtig, aber
es hilft Ihnen nicht viel weiter.
Eine andere Möglichkeit ist: „Der Konsum hängt vom Vermögen ab.“ Auch
das ist richtig, aber nicht vollständig. Das Schaubild sagt Ihnen viel mehr als
das.
Ein guter Satz wäre „Der Konsum nimmt zu, wenn das Vermögen zunimmt,
aber die Steigung des Konsums wird immer geringer, je größer das Vermögen ist.“
Kurvenverlauf
Manchmal ist es notwendig, die tatsächliche Steigung einer Geraden oder
die Steigung entlang einer Kurve zu berechnen. Viele haben in der Schule
28
1 Grundlagen der Volkswirtschaftslehre: Mathematik und grafische Darstellungen
eine Formel zur Berechnung einer Steigung gelernt: „die Steigung ist gleich
dem Verhältnis von Höhe zur Länge“ oder
Steigung ¼
H€
ohe
L€ange
Diese Formel funktioniert hier auch. Die Höhe ist die Veränderung zwischen
zwei Punkten auf der senkrechten Achse. Die Länge ist der Abstand der beiden Punkte auf der waagrechten Achse.
Zwischen den Punkten A und B in Abb. 1.6 ist die „Höhe“ 6 – 4 = 2. Die
„Länge“ ist 3 – 2 = 1. Somit ist die Steigung zwischen A und B:
H€
ohe Δy 6 " 4 2
¼
¼
¼ ¼2
L€
ange Δx 3 " 2 1
(Zur Erinnerung: Δ ist der griechische Großbuchstabe „Delta“ und steht für
„Veränderung“.)
Positive oder negative Steigung
Wenn die Steigung, wie in Abbildung 1.6, positiv ist, dann sagen wir, dass die
zwei Variablen in direkter Beziehung stehen oder sich proportional verhaly
10
8
6
B
4
A
2
0
(x = 3, y = 6)
(x = 2, y = 4)
1
2
3
Abbildung 1.6 Berechnung einer positiven Steigung.
4
5
6
x
Grafische Darstellungen
29
y
10
8
6
4
2
0
1
2
3
4
5
6
x
Abbildung 1.7 Eine negative Steigung.
ten. Wenn die Temperatur ansteigt (wenn x steigt), trinken mehr Leute Limonade (y steigt). Wirtschaftswissenschaftler sagen: Temperatur und Limonadenkonsum verhalten sich proportional.
Wenn die Steigung negativ ist, so wie in Abb. 1.7, stehen die Variablen in
negativer Beziehung zueinander, sie verhalten sich umgekehrt proportional. Wenn die Temperatur steigt (wenn x steigt), kaufen weniger Menschen
Wollmäntel (y nimmt ab). Volkswirte sagen: Die Temperatur und der Verkauf
von Wollmänteln stehen in umgekehrter Beziehung zueinander.
Die Steigung einer Geraden zwischen zwei Punkten ist gleich der „Höhe dividiert durch die Länge“. Die Höhe ist die Veränderung des Werts auf der
senkrechten Achse. Die Länge ist die Veränderung des Werts auf der waagrechten Achse. Zwischen A und B steigt der Wert von y, das auf der senkrechten Achse abgetragen ist, von 4 auf 6. Die Höhe ist gleich Δy = 6 – 4 = 2.
Zwischen A und B steigt der Wert von x, der auf der waagrechten Achse abgetragen ist, von 2 auf 3. Die Länge ist gleich Δx = 3 – 2 = 1. Die Steigung
zwischen A und B ist Höhe/Länge = 2/1 = 2.
Wenn sich zwei Variablen umgekehrt proportional verhalten, wird das Verhältnis durch eine abwärts verlaufende Kurve dargestellt. Wenn die Variable,
die auf der waagrechten Achse abgetragen wird, steigt, nimmt die Variable
ab, die auf der senkrechten Achse abgetragen wird.
30
1 Grundlagen der Volkswirtschaftslehre: Mathematik und grafische Darstellungen
Aufgabe
1.3
Was ist die Steigung in Abb. 1.7?
Eine Kurve kann eine Gerade sein, manchmal auch lineare Kurve genannt.
Die Steigung auf einer Geraden ist immer dieselbe, egal welche Punkte zur
Berechnung verwendet werden. Die Steigung ist konstant.
Nichtlineare Kurven
Eine Kurve kann auch gekrümmt statt gerade sein. Eine Kurve, die keine Gerade ist, wird manchmal auch nichtlineare Kurve genannt. Die Steigung auf
einer nichtlinearen Kurve ändert sich. Abb. 1.8a zeigt einen positiven und
wachsenden Verlauf: y steigt wenn x steigt, und die Steigung von y wird
immer größer je mehr x steigt. Die Steigung zwischen den Punkten C und D
ist größer als die Steigung zwischen den Punkten A und B.
Abb. 1.8b zeigt eine positive, aber abnehmende Steigung: y steigt, wenn x
steigt; aber die Steigung y wird umso geringer, je mehr x steigt. Die Steigung
zwischen den Punkten C und D ist geringer als die Steigung zwischen den
Punkten A und B.
y
Steigung zwischen
C & D = 5/3
Länge = 3
D
Steigung zwischen
A & B = 1/3
Höhe = 5
Höhe = 1
Länge = 3
A
C
B
Abbildung 1.8a Positive und wachsende Steigung.
x
Grafische Darstellungen
31
y
Länge = 3
Höhe = 1
D
C
Länge = 3
B
Steigung zwischen
C & D = 1/3
Höhe = 5
A
Steigung zwischen
A & B = 5/3
x
Abbildung 1.8b Positive und abnehmende Steigung.
Abb. 1.8c zeigt einen negativen und wachsenden (als absoluter Wert) Verlauf:
y sinkt wenn x steigt; und die Steigung y sinkt je mehr x steigt. Abb. 1.8 wird
auch als konkav zum Nullpunkt bezeichnet. Die Steigung zwischen den
y
A
Höhe = −1
B
Länge = 3
C
Steigung zwischen
A & B = −1/3
Höhe = −5
Steigung zwischen
C & D = −5/3
D
Länge = 3
x
Abbildung 1.8c Negative und zunehmende Steigung.
32
1 Grundlagen der Volkswirtschaftslehre: Mathematik und grafische Darstellungen
y
A
Höhe = −5
Steigung zwischen
A & B = −5/3
B
Länge = 3
Steigung zwischen
C & D = −1/3
C
Höhe = −1
Länge = 3
D
x
Abbildung 1.8d Negative und abnehmende Steigung.
Punkten C und D ist größer (als absoluter Wert) als die Steigung zwischen
den Punkten A und B.
Die Abb. 1.8d zeigt einen negativen aber abnehmenden (als absoluter Wert)
Verlauf: y sinkt, wenn x steigt; und die Steigung y nimmt ab, je mehr x steigt.
Abb. 1.8d wird auch als konvex zum Nullpunkt bezeichnet. Die Steigung
zwischen den Punkten C und D ist geringer (als absoluter Wert) als die Steigung zwischen den Punkten A und B.
Der Verlauf dieser Kurve ist positiv – der Wert von y steigt, wenn der Wert
von x steigt. Die Steigung wird größer, wenn wir uns von links nach rechts
auf der Kurve bewegen. Zwischen den Punkten A und B beträgt die Steigung
1/3. Zwischen den Punkten C und D beträgt die Steigung 5/3.
Der Verlauf dieser Kurve ist positiv – der Wert von y steigt, wenn der Wert
von x steigt. Die Steigung wird kleiner, wenn wir uns von links nach rechts
auf der Kurve bewegen. Zwischen den Punkten A und B beträgt die Steigung
5/3. Zwischen den Punkten C und D beträgt die Steigung 1/3.
Der Verlauf dieser Kurve ist negativ – der Wert von y sinkt, wenn der Wert
von x steigt. Die Steigung wächst als absoluter Wert, wenn wir uns von links
nach rechts auf der Kurve bewegen. Zwischen den Punkten A und B beträgt
die Steigung –1/3. Zwischen den Punkten C und D beträgt die Steigung –5/3.
Kurven mit negativer und wachsender Steigung werden auch „konkav zum
Nullpunkt“ genannt.
Grafische Darstellungen
33
Der Verlauf dieser Kurve ist negativ – der Wert von y sinkt, wenn der Wert
von x steigt. Die Steigung nimmt als absoluter Wert ab, wenn wir uns von
links nach rechts auf der Kurve bewegen. Zwischen den Punkten A und B
beträgt die Steigung –5/3. Zwischen den Punkten C und D beträgt die Steigung –1/3. Kurven mit negativer und abnehmender Steigung werden auch
„konvex zum Nullpunkt“ genannt.
Aufgaben
Sie sollten in der Lage sein, mühelos zwischen Wortformulierungen und grafischen Darstellungen zu wechseln. Versuchen Sie folgende Aussagen grafisch darzustellen:
1.4
Die nachgefragte Menge nimmt ab, wenn der Preis steigt (senkrechte Achse:
Preis; waagrechte Achse: nachgefragte Menge).
1.5
Der Konsum nimmt zu, wenn das Vermögen steigt, aber der Konsum wächst
um so weniger, je höher das Vermögen ist (senkrechte Achse: Konsum;
waagrechte Achse: Vermögen).
1.6
Mit der Erhöhung der Zahl der Arbeitskräfte steigt das Grenzprodukt zunächst, nimmt dann aber ab (senkrechte Achse: Grenzprodukt; waagrechte
Achse: Zahl der Arbeitskräfte).
1.7
Das Einkommen entspricht immer den gesamten Ausgaben (senkrechte Achse: Gesamtausgaben; waagrechte Achse: Einkommen).
1.8
Wenn die Arbeitslosenquote niedrig ist, ist die Inflationsrate hoch; aber
wenn die Arbeitslosenquote hoch ist, ist die Inflationsrate niedrig (senkrechte Achse: Inflationsrate; waagrechte Achse: Arbeitslosenquote).
1.9
Die angebotene Menge steigt, wenn der Preis steigt (senkrechte Achse: Preis;
waagrechte Achse: angebotene Menge).
34
1 Grundlagen der Volkswirtschaftslehre: Mathematik und grafische Darstellungen
1.10
Für einen Monopolisten hat der Grenzerlös, wenn die Menge steigt, einen
steileren negativen Verlauf als der Durchschnittserlös (senkrechte Achse:
Grenzerlös und Durchschnittserlös; waagrechte Achse: Menge). (Sie müssen
zwei Kurven zeichnen.)
1.11
Wenn die Menge an produzierter Butter von 2.000 auf 1.900 Einheiten gesenkt wird, steigt die Zahl an produzierten Waffen von 10 auf 20 Einheiten.
Aber wenn die Menge an produzierter Butter von 1.000 auf 900 Einheiten gesenkt wird, steigt die Zahl an produzierten Waffen nur von 80 auf 82 Einheiten (senkrechte Achse: Einheiten produzierter Butter; waagrechte Achse: Einheiten produzierter Waffen).
1.12
Die angebotene Menge ist 13, wenn der Preis 5 ist. Aber wenn der Preis 8
beträgt, ist die angebotene Menge 19 (senkrechte Achse: Preis; waagrechte
Achse: Angebotsmenge).
p
pA
p
A
B
pB
p
A
B
N
xA
xB
(a)
x
N2
N1
xA
xB
x
(b)
Abbildung 1.9 (a) Bewegung auf einer Kurve im Gegensatz zu der (b) Verschiebung einer Kurve.
Grafische Darstellungen
35
1.13
Wenn der Preis 5 beträgt, ist die nachgefragte Menge 40. Aber wenn der Preis
10 beträgt, ist die nachgefragte Menge 39 (senkrechte Achse: Preis; waagrechte Achse: nachgefragte Menge).
Tipp
Zeichnen Sie immer eine kleine Grafik, wenn Sie etwas über das Verhältnis zwischen zwei
Variablen lesen.
Wenn wir uns zwischen zwei Punkten bewegen, bewegen wir uns „auf“ oder
auch „entlang“ einer bestehenden Kurve. In Abb. 1.9a bewegen wir uns auf
der Kurve von A nach B, wenn der Preis p sinkt, zu einer größeren Menge x.
Wenn eine vollkommen neue Kurve entsteht, „verschiebt sich die Kurve“. In
Abb. 1.9b gibt es für jeden Preis p eine Steigung der Menge x und so ergibt
sich eine komplett neue Kurve N2.
Bewegung auf einer Kurve im Gegensatz zur Verschiebung einer Kurve
Volkswirte unterscheiden gerne zwischen der Bewegung auf einer Kurve
und der Verschiebung einer Kurve. Wenn wir uns „auf“ oder „entlang“
einer Kurve bewegen, bewegen wir uns zwischen zwei Punkten auf einer bestehenden Kurve. In Abb. 1.9a verändert sich die Menge von x1 zu x2, wenn
der Preis sich von p1 zu p2 ändert. Wir bewegen uns auf der bestehenden
Kurve.
Wenn sich die Kurve „verschiebt“, verändert sich das gesamte Verhältnis
zwischen den beiden Variablen. In Abb. 1.9b verschiebt sich die Kurve von
N1 nach N2, wenn zu jedem Preis die Menge steigt. Damit erhalten wir eine
völlig neue Kurve. Manchmal ist es zur Unterscheidung hilfreich, die neue
Kurve dunkler als die ursprüngliche Kurve einzuzeichnen.
Ein einfacher Weg, um herauszufinden, ob wir uns auf einer Kurve bewegen
oder sich die Kurve verschiebt, ist folgender: Wenn sich eine unabhängige
Variable, die auf einer der Achsen abgetragen ist, verändert, bewegen wir
uns auf der bestehenden Kurve. Aber wenn sich eine unabhängige Variable
verändert, die nicht an einer der Achsen abgetragen ist, verschiebt sich die
gesamte Kurve.
36
1 Grundlagen der Volkswirtschaftslehre: Mathematik und grafische Darstellungen
Zusammenfassung
Dieses Kapitel hat Ihnen einen Überblick über die mathematischen Grundlagen, die in der Volkswirtschaftslehre verwendet werden, gegeben. Lesen
Sie in diesem Kapitel die Informationen über die einzelnen Hilfsmittel nach,
wenn Sie im Kurs eingeführt und verwendet werden. Wenn Sie weiterhin
Probleme haben sollten, hilft es vielleicht, in einem Mathematikbuch Details
nachzulesen. Wir sind jetzt bereit, in die Tiefen der Volkswirtschaftslehre
einzutauchen.