UE10 20150611 Angabe

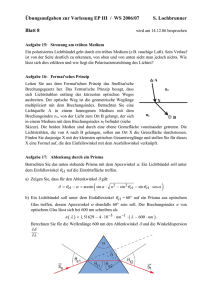
Institut f. Angewandte Physik
UE Grundlagen der Physik II SS 2015
10. Übung am 11. 6. 2015
47) In einer stark gekrümmten optischen Faser (Durchmesser
d, Brechungsindex n) können einige Lichtstrahlen, die auf der
Innenseite der Faser treffen, aus der Faser entweichen, statt in
das Innere reflektiert zu werden (siehe Abbildung). Wie groß
muss der Krümmungsradius eins kurzen gebogenen
Abschnitts mindestens sein, damit die Totalreflexion der
Lichtstrahlen gewährleistet ist, wenn diese anfänglich parallel
zur Achse der Faser verlaufen?
(1 Pkt)
48) Auf die ebene Fläche eines Halbzylinders mit Radius r aus
Glas mit dem Brechungsindex n = 2 fallen Lichtstrahlen. Sie
liegen in einer Ebene senkrecht zur Zylinderachse und treffen auf
die ebene Fläche unter dem Einfallswinkel ! = 45° auf.
An welchen Stellen der Mantelfläche des Halbzylinders treten
Lichtstrahlen aus ?
(2 Pkte)
49) Ein Material habe im Infraroten eine Absorptionslinie bei der Kreisfrequenz ! 0 . Der
Brechungsindex lässt sich außerhalb der Resonanzlinie näherungsweise durch
n ! A + B / (" 0 # " ) mit den Konstanten A und B darstellen.
2
2
Berechnen Sie die Phasen und die Gruppengeschwindigkeit.
(2 Pkte)
!
" + $ )] mit der
50) Eine linear polarisierte Welle der Form E = x̂ ! E 0 exp [ i (" t # kz
Vakuumfrequenz ! = 5 " 10 ! Hz falle bei z=0 senkrecht auf ein homogenes Material mit dem
14
0
komplexen Brechungsindex n! = 3.0 ! i " 0.15 bei dieser Frequenz.
a) Wie groß sind Kreisfrequenz, Wellenlänge und Phasengeschwindigkeit des Lichtstrahls im
Vakuum und im Medium?
1
b) Wie viel Prozent der! Intensität
! der Strahlung wird an der Grenzfläche reflektiert?
c) Bestimmen sie die E - und B -Felder im Medium
d) In welcher Tiefe ist die Intensität der Strahlung auf den
! 1/e-ten Teil abgesunken?
!
e) Bestimmen sie den Phasenwinkel zwischen E - und B -Feld im Material.
(2 Pkte)
51) Der Regenbogen kann durch die Reflexion des Sonnenlichtes im Inneren der Regentropfen
erklärt werden. Ein monochromatischer Lichtstrahl (Bestandteil des Bündels weißen Lichtes) trifft
auf einen kugelförmigen Regentropfen mit Brechungsindex n und wird im Inneren des Tropfens
(total) reflektiert (siehe Abbildung).
a) Wie groß ist der Ablenkwinkel δ in Abhängigkeit vom Einfallswinkel α und dem ersten
Brechungswinkel β ?
b) Bestimmen Sie den Wert von sin(α) als Funktion von n, für den δ minimal wird und berechnen
Sie Φ=π-δ für n=1.33 (Wasser).
c) Die Intensität des austretenden Lichtes hat ihr Maximum, wenn die Ablenkung δ des eintretenden
Lichtes minimal ist. Erklären Sie vor diesem Hintergrund die Bildung des Regenbogens durch
weißes Licht. Hierzu nehmen wir an, dass der Brechnungsindex wie folgt von der Lichtwellenlänge
λ abhängt (Gesetz von Cauchy):
n( ! ) = n0 + C ! , wobei n0 und C zwei positive Konstanten sind.
2
(3 Pkte)
2