P1b:¨Ubungen zur Geometrischen Optik, SS 2010
Werbung

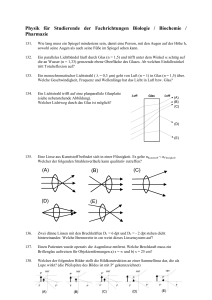
P1b: Übungen zur Geometrischen Optik, SS 2010 Blatt3, Abgabetermin: Mi. 12.05.2010 (in der Vorlesung) 1. Gegeben sei der in der Vorlesung demonstrierte Aufbau (siehe Abb.): Eine dünne, symmetrisch bikonvexe Linse (nL = 1.5) befinde sich am unteren Ende eines Kunststoff-Rohres. Ein Gegenstand G, welcher sich in 21 cm Entfernung unterhalb der Linse befindet, wird auf einen Schirm oberhalb der Linse mit 20facher Vergrößerung scharf abgebildet. Nun wird Wasser (nW = 1.33) in das Rohr gefüllt, bis die Linse gerade komplett bedeckt ist. (a) Was lässt sich beim Einfüllen des Wassers auf dem Schirm beobachten? (b) Geben Sie für den Aufbau mit Linse und Wasser die Systemmatrix M̂ an! (c) Um wieviel Dioptrien hat sich die Brechkraft des Systems durch das Wasser geändert und in welchem Bildabstand b 0 würde man jetzt eine scharfe Abbildung des Gegenstandes G erwarten? (Hinweis: Die Brechkraft (in Dioptrien) ist gleich dem Kehrwert der Brennweite (in Metern)). (d) Wieweit muss der Gegenstand G verschoben werden, um auf dem Schirm in seiner ursprünglichen Position eine scharfe Abbildung zu erhalten und wie ist dabei die Vergrößerung? (e) Wie ändern sich die Abbildungseigenschaften des Systems, wenn man das Rohr bis auf eine endliche Höhe d über dem oberen Scheitel der Linse mit Wasser auffüllt? 2. Paralleles Licht soll mit einer dünnen plankonvexen Linse auf einen Punkt fokussiert werden. Die plane Seite sei auf der Einfallsseite. Berechnen Sie mit dem Fermatschen Prinzip die Form der gekrümmten Oberfläche. (Hinweis: Paralleles Licht = Licht welches aus einer (Punkt)quelle im Unendlichen kommt. Damit Licht, welches von einem Punkt ausgeht, wieder in einem Punkt vereinigt wird, müssen nach dem Fermatschen Prinzip die optischen Weglängen für alle Strahlen gleich sein.) 3. Ein Laserresonator besteht aus zwei shärischen Spiegeln, zwischen denen das Licht eingesperrt wird. Ein solcher Resonator befindet sich in einem stabilen Zustand, wenn Lichtstrahlen, die unter einem kleinen Winkel zur optischen Achse laufen, nach mehrfacher Reflexion innerhalb des Resonators bleiben. Die Frage ist, wie muss der der Resonator beschaffen sein (Abstand zwischen den Spiegeln d, Krümmungsradien R1 , R2 ), damit ein stabiler Zustand erreicht wird. c für eine Periode des Lichtumlaufes auf! (a) Stellen Sie dazu die Systemmatrix M 1 c. Dadurch werden die Vektoren (h,β) in die neuen (b) Diagonalisieren Sie die Matrix M Vektoren (ah + bβ, −bh + aβ) überführt. cN . Die bündeln(c) Für N Perioden des Lichtumlaufes ergibt sich die Systemmatrix zu M d den Eigenschaften lassen sich leichter an Hand der diagonalisierten Matrix M D erN d kennen. Berechnen Sie MD und stellen Sie die Transfergleichung für die Vektoren (ahN + bβN , −bhN + aβN ) für N Perioden des Lichtumlaufes auf! (d) Überlegen Sie sich, wie die Eigenwerte beschaffen sein müssen (reell oder komplex), damit nach N Umläufen des Strahls hN endlich bleibt und somit das Licht im Resonator verbleibt! Leiten Sie daraus eine Bedingung für d, R1 , R2 für einen stabilen Zustand des Resonators ab! 2