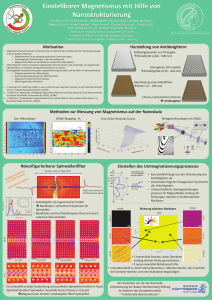
Wellenvektoraufgelöste Brillouin

Wellenvektoraufgelöste
Brillouin-Lichtstreuspektroskopie
an nichtlinearen Spinwellen
DIPLOMARBEIT
in
Experimentalphysik
von
Matthias Benjamin Jungfleisch
durchgeführt am
Fachbereich Physik
der Technischen Universität Kaiserslautern
Unter Anleitung von
Prof. Dr. Burkard Hillebrands
November 2009
für meine Eltern
Inhaltsverzeichnis
1
Einleitung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1
2
Theoretische Grundlagen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
2.1 Ferromagnetismus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
2.1.1 Dipol-Dipol-Wechselwirkung und Entmagnetisierungsfeld . . . . . . . . . . . . . . . . .
3
2.1.2 Austauschwechselwirkung. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5
2.2 Spindynamik. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
2.2.1 Landau-Lifshitz-Gilbert-Gleichung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
2.3 Spinwellen. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9
2.3.1 Magnetostatische Oberflächenmoden . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
2.3.2 Magnetostatische Backward-Volumenmoden. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
2.4 Parametrische Prozesse . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
2.4.1 Erzwungene Verstärkung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
2.4.2 Parametrische Verstärkung. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
3
Experimenteller Aufbau . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
3.1 Yttrium-Eisen-Granat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
3.2 Probenaufbau . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
3.3 Mikrowellenaufbau . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
3.3.1 Direkte Anregung von Spinwellen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
3.3.2 Parametrische Verstärkung. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
3.4 Frequenzmessung mittels Interferometrie. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
3.4.1 Fabry-Perot-Interferometer . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
3.4.2 Tandem-Fabry-Perot-Interferometer . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
3.5 Brillouin-Lichtstreuspektroskopie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
3.5.1 Zeitaufgelöste Brillouin-Lichtstreuspektroskopie. . . . . . . . . . . . . . . . . . . . . . . . . . . 33
3.5.2 Wellenvektoraufgelöste Brillouin-Lichtstreuspektroskopie . . . . . . . . . . . . . . . . . 34
i
INHALTSVERZEICHNIS
4
Experimentelle Ergebnisse und Diskussion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
4.1 Direkte oder erzwungene Anregung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
4.1.1 Backward-Volumenmoden . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
4.1.2 Oberflächen- oder Damon-Eshbach- Moden. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
4.1.3 Untersuchung der Charakteristik verschiedener Antennen . . . . . . . . . . . . . . . . . . 42
4.2 Parametrische Verstärkung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44
4.2.1 Untersuchung des Minimums des Spinwellenspektrums . . . . . . . . . . . . . . . . . . . . 44
4.2.2 Untersuchung der dominanten Gruppe bei halber Pumpfrequenz . . . . . . . . . . . 50
4.2.3 Untersuchung der Abhängigkeit des angelegten Magnetfeldes vom Wellenvektor im Fall der dominanten Gruppe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53
5
Zusammenfassung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 58
Literaturverzeichnis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 60
Danksagung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 65
ii
Abbildungsverzeichnis
2.1
Präzession der Magnetisierung . . . . . . . . . . . . . . . . . . . . . . . . . . . .
8
2.2
Dipolare Spinwellendispersion . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
2.3
Streufelder der dynamischen Magnetisierung bei dipolaren Spinwellen . . . . . . . 13
2.4
Dispersion von Spinwellen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
2.5
Veranschaulichung der erzwungenen Verstärkung . . . . . . . . . . . . . . . . . . 15
2.6
Instabilitäten bei parametrischen Prozessen . . . . . . . . . . . . . . . . . . . . . 17
2.7
Butterfly-Kurve . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
2.8
Parametrische Anregung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
3.1
Yttrium-Eisen-Granat Kristallstruktur . . . . . . . . . . . . . . . . . . . . . . . . 21
3.2
Aufbau der Probe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
3.3
Veranschaulichung des Lift-off-Prozesses . . . . . . . . . . . . . . . . . . . . . . 23
3.4
Mikroskopaufnahmen der angfertigten Antennen . . . . . . . . . . . . . . . . . . 24
3.5
Oerstedfeld einer Microstrip-Antenne . . . . . . . . . . . . . . . . . . . . . . . . 25
3.6
Schematische Darstellung des Mikrowellenaufbaus . . . . . . . . . . . . . . . . . 26
3.7
Aufbau eines Fabry-Perot-Interferometers . . . . . . . . . . . . . . . . . . . . . . 27
3.8
Tandem-Fabry-Perot-Interferometer . . . . . . . . . . . . . . . . . . . . . . . . . 28
3.9
Aufbau des Interferometer . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
3.10 Grundlage der Brillouin-Lichtstreuspektroskopie . . . . . . . . . . . . . . . . . . 30
3.11 Typische BLS Streugeometrien . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
3.13 Grundlage der zeitaufgelösten Brillouin-Lichtstreuspektroskopie . . . . . . . . . . 33
3.14 Aufbau zur wellenvektoraufgelösten BLS . . . . . . . . . . . . . . . . . . . . . . 35
3.15 Wellenvektorabhängige Untersuchung von Spinwellen mittels Blende . . . . . . . 36
iii
ABBILDUNGSVERZEICHNIS
3.16 Weitere Methoden zur wellenvektoraufgelösten Detektion von Spinwellen . . . . . 37
4.1
Backward-Volumenmode . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
4.2
Damon-Eshbach-Mode . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
4.3
Antennencharakteristik . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
4.4
Wellenvektoraufgelöste Untersuchung des Bose-Einstein-Kondensats . . . . . . . . 45
4.5
Abhängigkeit des Bose-Einstein-Kondensats von der Mikrowellenleistung . . . . . 46
4.6
Magnetfeldabhängigkeit des Signals vom Minimum des Spinwellenspektrums . . . 47
4.7
Auswertung der zeitaufgelösten Messung . . . . . . . . . . . . . . . . . . . . . . 48
4.8
Zeitaufgelöste Messung des Signals vom Minimum des Spinwellenspektrums . . . 49
4.9
Abhängigkeit der dominaten Gruppe von der Mikrowellenleistung . . . . . . . . . 50
4.10 Zeitliche Entwicklung des Spinwellensignals . . . . . . . . . . . . . . . . . . . . 51
4.11 Wellenvektoraufgelöste Untersuchung der dominanten Gruppe . . . . . . . . . . . 52
4.12 Abhängigkeit des angelegten Magnetfeldes vom Wellenvektor um Fall der dominanten Gruppe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53
4.13 Hybridisierung von magnonischer und phononischer Dispersion . . . . . . . . . . 56
4.14 Hybridisierung zwischen Phononen und Spinwellen bei Veränderung der Pumpfrequenz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57
iv
KAPITEL 1
Einleitung
Nicht erst seit der Verleihung des Nobelpreises in Physik im Jahr 2007 an Peter Grünberg und
Albert Fert für die Entdeckung des Riesenmagnetowiderstandes [1–3] rückt das Forschungsgebiet Magnetismus in das öffentliche Interesse. Viele alltägliche Tätigkeiten lassen sich heute ohne
nichtflüchtige magnetische Speichermedien, wie Festplatten oder Magnetstreifen auf Kreditkarten, kaum mehr vorstellen. Die wachsenden Anforderungen im Bereich der Datenverarbeitung
und der Telekommunikation führten - und führen - zu einer rasanten Entwicklung magnetischer
Systeme. Die Datenspeicherung mittels Festplatte stellt jedoch nicht die einzige Anwendung des
Magnetismus dar. Die Entwicklung des MRAM (Magnetic Random Access Memory) zeigt, dass
es möglich ist hohe Zugriffsgeschwindigkeiten eines herkömmlichen auf Halbleitertechnik basierenden Arbeitsspeichers mit der Nichtflüchtigkeit einer Festplatte zu verbinden [4, 5].
Seit den ersten Untersuchungen von Spinwellen in Yttrium-Eisen-Granat (YIG) durch
J. R. Eshbach im Jahr 1962 [6] wurde der Erforschung von Spinwellen zunehmend Aufmerksamkeit geschenkt. Die Spinwelleneigenschaften hängen von einer Vielzahl von Materialparametern
ab, die mittels Untersuchungen des thermischen Spinwellenspektrums bestimmt werden können.
Heute verwendet man solche Messungen zum Beispiel, um Heusler-Legierungen zu charakterisieren [7].
Des Weiteren können Spinwellen – wie in dieser Arbeit – künstlich durch Mikrowellen angeregt
werden. Oftmals kommt bei Spinwellen-Experimenten als Material YIG zum Einsatz, in dem sich
Spinwellen aufgrund seiner sehr geringen Dämpfung über makroskopische Distanzen ausbreiten
können. Aus diesem Grund findet YIG auch Anwendung in vielen Mikrowellenbauteilen, die zur
analogen Signalverarbeitung dienen [8].
In der Halbleitertechnologie setzte man bisher lediglich die Ladung des Elektrons als Informationsträger ein. In den letzten Jahren versuchte man dagegen den Spin des Elektrons zur Informationsdarstellung und -verarbeitung zu verwenden. Durch die Berücksichtigung des Spins erhoffte
man sich komplett neuartige Bauelemente entwickeln zu können. So wurden verschiedene Konzepte zur Realisierung von logischen Operatoren mit Hilfe von Spinwelleninterferometern vor-
1
gestellt [9–11]. Darüber hinaus wurde von A. Khitun et al. ein Modell vorgeschlagen, bei dem
Spinwellen in Quantencomputern verwendet werden [12].
Spinwellen können im quantenmechanischen Teilchenbild als Magnonen betrachtet werden. Sie
haben ganzzahligen Spin und können in einem thermischen Gleichgewicht durch die Bose-EinsteinStatistik beschrieben werden. In YIG dienen sie als Modellsystem für ein bosonisches Gas. Im Jahr
2006 demonstrierte S. O. Demokritov in Kooperation mit B. Hillebrands, dass es möglich ist, ein
Bose-Einstein-Kondensat in einem Magnonengas bei Raumtemperatur zu erzeugen [13].
Die Brillouin-Lichtstreuspektroskopie ist seit den 1970er Jahren ein etabliertes Beobachtungsinstrument sowohl zur Detektion von Spinwellen als auch von Phononen. Prinzipiell ist es hiermit
möglich orts-, zeit- und phasenaufgelöst Spinwellen zu beobachten [14, 15].
Im Rahmen dieser Diplomarbeit wurden mikrowellenangeregte Spinwellen in YIG wellenvektoraufgelöst mit Hilfe der Brillouin-Lichtstreuspektroskopie untersucht. In Kapitel 2 wird ein kurzer Überblick über die physikalischen Grundlagen gegeben, die für das Verständnis der in dieser
Arbeit verwendeten Messmethoden und der vorgestellten Ergebnisse erforderlich sind. Zunächst
wird auf die fundamentalen Phänomene des Ferromagnetismus eingegangen und anschließend die
Landau-Lifshitz und Gilbert-Gleichung halbklassisch hergeleitet. Außerdem werden die verschiedenen Spinwellenmoden erläutert und die grundlegenden Prozesse der parametrischen Verstärkung
eingeführt.
Auf den experimentellen Aufbau wird in Kapitel 3 eingegangen. Hier wird das untersuchte Material – YIG – näher beschrieben sowie der Probenaufbau vorgestellt. Des Weiteren werden der
verwendete Mikrowellenaufbau und die Grundlagen der Brillouin-Lichtstreuspektroskopie (BLS)
erklärt. Dabei liegt ein besonderes Augenmerk auf dem neu entwickelten Aufbau zur wellenvektorabhängigen Messung von Spinwellen.
In Kapitel 4 werden die durchgeführten Messungen präsentiert. Anhand der Ergebnisse, die bei
der direkten Anregung von Spinwellen gewonnen wurde, wird demonstriert, dass sich der Aufbau
prinzipiell zur wellenvektoraufgelösten BLS eignet. Im Anschluss daran werden die Resultate der
parametrischen Verstärkung vorgestellt: Sowohl die wellenvektoraufgelöste Messung des BoseEinstein-Kondensats als auch die Untersuchungen der dominanten Gruppe werden besprochen.
Die Arbeit schließt in Kapitel 5 mit einer Zusammenfassung der erzielten Ergebnisse und einem
kleinen Ausblick auf weiterführenden Untersuchungen, die von dieser Arbeit ausgehen.
2
KAPITEL 2
Theoretische Grundlagen
Im Folgenden sollen die theoretischen Grundlagen, die für das Verständnis der hier präsentierten
Ergebnisse erforderlich sind, vorgestellt werden. Alle hier vorgestellten Gleichungen sind im cgsSystem angegeben. Die Umrechnung vom cgs- ins SI-System findet sich beispielsweise in [16].
Zunächst werden die Grundlagen des Ferromagnetismus erläutert und auf die fundamentale Gleichung der Spindynamik – die Landau-Liftshitz- und Gilbert-Gleichung – eingegangen.
Nachdem die Spindynamik besprochen wurde, wird ein kurzer Überblick über die allgemeinen
Eigenschaften von Spinwellen gegeben. Spinwellen können als kollektive Anregung aller Spins
interpretiert werden, die sich im Festkörper in Form von Wellen ausbreiten. Je nach Größe des
Wellenvektors unterscheidet man zwischen austauschdominierten bzw. dipoldominierten Spinwellen. Im letzten Abschnitt des Kapitels werden die unterschiedlichen Arten von Spinwellen charakterisiert und die entsprechenden Dispersionsrelationen hergeleitet.
2.1. Ferromagnetismus
Der ferromagnetische Grundzustand ist durch eine Parallelstellung der Spinmomente gekennzeichnet. Oberhalb einer materialspezifischen Temperatur, der sogenannten Curie Temperatur, verliert
der Festkörper seine ferromagnetische Ordnung und wird paramagnetisch.
Die einzelnen Spinmomente koppeln untereinander im Wesentlichen aufgrund zwei verschiedener
Wechselwirkungsmechanismen: der Dipol-Dipol-Wechselwirkung und der Austauschwechselwirkung. Darauf wird im Folgenden näher eingegangen.
2.1.1 Dipol-Dipol-Wechselwirkung und Entmagnetisierungsfeld
Die Spins, welche als magnetische Dipole betrachtet werden können, wechselwirken miteinander.
Die Wechselwirkungsenergie zwischen zwei magnetischen Dipolmomenten µk und µl im Abstand
3
2.1 Ferromagnetismus
rkl ist dann [17]
µk µl
(µk rkl )(µl rkl )
.
(2.1)
3 −3
|rkl |
|rkl |5
Die Dipol-Dipol-Wechselwirkung ist langreichweitig, so dass in einem Festkörper über alle Atome
Ed =
summiert werden muss.
Handelt es sich um einen unendlich ausgedehnten, homogen magnetisierten Festkörper, so kompensieren sich alle atomaren magnetischen Momente gegenseitig [18]. Für einen endlichen Festkörper
ist dies nicht mehr der Fall. Durch die nicht kompensierten Dipolfelder an der Oberfläche entsteht
ein Dipolfeld, welches Entmagnetisierungsfeld Hd genannt wird. Zur Berechnung dieses Feldes
verwendet man die magnetostatischen Maxwellgleichungen. Das ist erlaubt, da die Frequenzen
aller hier behandelten Spinwellen deutlich kleiner als die Frequenz von Licht des gleichen Wellenvektors ist [19, 20]. In der Magnetostatik vereinfachen sich die Maxwellgleichungen zu
∇ × Hd = 0
(2.2)
∇ · B = ∇ · (Hd + 4πM) = 0 .
(2.3)
Wegen der Rotationsfreiheit des Entmagnetisierungsfeldes (Gleichung (2.2)) ist es möglich ein
skalares Potential ΦM zu definieren mit
Hd = −∇ΦM
.
(2.4)
Setzt man Gleichung (2.4) in Gleichung (2.3) ein, erhält man die Poissongleichung
∆ΦM = −4π(∇ · M) = −ρM
(2.5)
mit der magnetische Ladungsdichte ρM = ∆ΦM . Lösung dieser Gleichung ist das aus der Elektrodynamik [17] bekannte Poisson-Integral
Z
Z
∇′ · M(r′ ) ′
ρM
1
′
dr
=
−
dr
ΦM (r) =
4π
|r − r′ |
|r − r′ |
.
(2.6)
Für endliche Magnetisierungsverteilungen lässt sich das Integral lösen und kann in einen Volumensowie einen Oberflächenterm aufgeteilt werden:
I
Z
n(r′ ) · M(r′ ) ′
∇′ · M(r′ ) ′
′
dr
+
dF
ΦM (r ) = −
|r − r′ |
|r − r′ |
∂V
V
.
(2.7)
n(r′ ) bezeichnet dabei den Flächennormalenvektor. Der erste Term, welcher ein Volumenintegral
ist, beschreibt das magnetostatische Entmagnetisierungspotential durch eine inhomogene Magnetisierungsverteilung. Daher lassen sich magnetische Volumenladungen λM = ∇′ · M(r′ ) definieren. Genauso kann man sich den Oberflächenanteil von ΦM als durch Oberflächenladungen σM = n(r′ ) · M(r′ ) erzeugt vorstellen. Dieser Anteil beschreibt den Einfluss der geometrischen Begrenzungen des Materials. Geht man von einer homogenen Magnetisierung aus, so gilt
4
2.1 Ferromagnetismus
∇′ · M(r′ ) = 0, wodurch man für das Entmagnetisierungsfeld
I
n(r′ )
′
dF
Hd (r) = −∇ M ·
′
∂V |r − r |
(2.8)
erhält. Da das Entmagnetisierungsfeld Hd linear in der Magnetisierung M ist, kann es durch den
Entmagnetisierungstensor N (r)
Hd (r) = −4πN (r)M
(2.9)
ausgedrückt werden. Bei homogen magnetisierten Ellipsoiden ist der Entmagnetisierungstensor
unabhängig vom Ort [21]. Im Hauptachsensystem des Ellipsoiden kann der Entmagnetisierungstensor diagonalisiert werden. In Tabelle 2.1 sind die Diagonalelemente für verschiedene Körper
angegeben. Die magnetostatische Energiedichte ist gegeben durch
1
ǫd = Hd · M
2
.
(2.10)
Diese wird minimal, wenn keine magnetischen Ladungen erzeugt werden, da dann das Entmagnetisierungspotential und wegen (2.4) auch Hd minimal ist. Das heißt, dass die Magnetisierung
stets homogen im Volumen und tangential zur Oberfläche des Festkörpers ausgerichtet ist. Dies
ist natürlich nur dann der Fall, wenn keine anderen Effekte, wie zum Beispiel ein äußeres Feld,
andere Konfigurationen erzwingen.
Kugel
Zylinder parallel ez
Film in der xy-Ebene
Nxx
1/3
1/2
0
Nyy
1/3
1/2
0
Nzz
1/3
0
1
Tabelle 2.1: Diagonalelemente des Entmagnetisierungstensors N
2.1.2 Austauschwechselwirkung
Wie bereits im vorangegangenen Kapitel erwähnt, ist die Dipol-Dipol-Wechselwirkung im Vergleich zur Austauschwechselwirkung sehr klein. Schätzt man die Dipol-Dipol-Wechselwirkung
zwischen zwei benachbarten Momenten µ = µb in einem Abstand von 0,3 nm ab, so erhält man
Ed ≈ 1,3 · 10−6 eV , was einer thermischen Energie von 0,01 K entspricht. Vergleicht man diese Temperatur mit der Curie Temperatur eines typischen Ferromagneten (Eisen: 1043 K, Kobalt:
1388 K, Nickel: 627 K [18]) ist offensichtlich, dass die Dipol-Dipol-Wechselwirkung nicht die Ursache der ferromagnetischen Ordnung sein kann.
Die Austauschwechselwirkung ist eine rein quantenmechanische Wechselwirkung, die klassisch
nicht beschrieben werden kann. Elektronen sind Fermionen und ihre Gesamtwellenfunktion muss
aufgrund des Pauli-Prinzips antisymmetrisch sein. Bei einem Zwei-Elektronen-System sind deshalb nur Kombinationen aus einer symmetrischen Spinwellenfunktion (parallele Spins) mit einer
5
2.1 Ferromagnetismus
antisymmetrischen Ortswellenfunktion oder umgekehrt möglich. Die Elektronenaufenthaltswahrscheinlichkeit ist für beide Fälle unterschiedlich und führt damit zu verschiedenen Energiewerten.
Die Energiedifferenz zwischen paralleler und antiparaller Stellung der Spins wird als Austauschenergie bezeichnet. Sie lässt sich für ein Spinsystem im sogenannten Heisenberg Modell [20] durch
den Heisenberg-Hamilton-Operator
Hex = −2
n
X
Jijex Si · Sj
(2.11)
i6=j
beschreiben. Dabei bezeichnen Si und Sj die Spins. Der Ausdruck Jijex heißt Austauschintegral
und ist durch den Überlapp der Wellenfunktionen des i-ten und j-ten Atom bestimmt. Da nur die
Wellenfunktionen benachbarter Atome überlappen und die Elektronen-Aufenthaltswahrscheinlichkeiten sehr schnell abfallen, kann man direkt folgern, dass die Austauschwechselwirkung eine
kurzreichweitige Wechselwirkung ist. Dies erlaubt die Vereinfachung des Problems durch die Molekularfeldnäherung, bei der lediglich über nächste Nachbarn (n. N.) summiert wird
Eiex
= −2
n.N.
X
Jijex Si
· Sj = −2Si ·
j
n.N.
X
Jijex Sj
j
n.N.
2 µi X ex
=
·
J Sj
gµB j ij
.
(2.12)
Hierbei wurde berücksichtigt, dass zwischen Spin und magnetischem Moment die Beziehung
µi = gµB Si gilt. Damit kann man die Austauschenergie als Zeemanenergie des magnetischen Moments µi im sogenannten Austauschfeld
Hex
n.N.
2 X ex
J Sj
=−
gµB j ij
(2.13)
auffassen. Nicht immer ist die Formulierung (2.12) für konkrete Rechnungen sinnvoll. Bei der quasiklassischen Beschreibung der Austauschwechselwirkung geht man daher von diskreten Spins zu
einer kontinuierlichen Magnetisierung über. Dazu ersetzt man den quantenmechanischen Drehimpuls durch einen Vektor mit beliebiger Orientierung. Sind alle Atome identisch und handelt es sich
um ein kubisches Gitter, so kann man die quasiklassische Austauschwechselwirkung als
Eex = −2Jex zS
2
n.N.
X
cos φij
(2.14)
i6=j
schreiben, wobei φij den Winkel zwischen zwei Spins und z die Anzahl der nächsten Nachbarn
bezeichnet. Mit Hilfe des Kosinussatzes
|Sj − Si |2 = S 2 + S 2 − 2S 2 · cos φij
(2.15)
ergibt sich
Eex = −2Jex zS 2
n.N.
X
i6=j
(1 −
1
|Sj − Si |2 ) .
S2
(2.16)
6
2.2 Spindynamik
Der erste Summand ist konstant und beschreibt die Energie, bei der die Spins parallel ausgerichtet sind. Durch geschickte Wahl des Energienullpunktes ist es möglich, ihn zum Verschwinden
zu bringen. Den Übergang zur makroskopischen Magnetisierung liefert die erste Ordnung einer
Taylorentwicklung
1
1
|Sj − Si | =
|(rij · ∇)M| ,
(2.17)
S
Ms
wobei rij der Ortsvektor vom Gitterplatz i zum Gitterplatz j ist. Es muss also immer noch über
einzelne Gitterplätze summiert werden, so dass man von der Summe (2.16) zu einem Integral der
Form
Eex =
mit der Energiedichte
ǫ=
Z
ǫd3 r
2A
2A
(∇ · M)2 = 2 M · ∆M
2
Ms
Ms
(2.18)
(2.19)
übergeht. Dabei bezeichnet A = zJS 2 /a die Austauschkonstante mit der Gitterkonstante a. Für
das gesuchte Austauschfeld erhält man
Hex = −∇M ǫ =
2A 2
∇ M = λex ∇2 M
Ms
mit der Austausch-Steifigkeitskonstanten λex =
(2.20)
2A
.
Ms
2.2. Spindynamik
2.2.1 Landau-Lifshitz-Gilbert-Gleichung
Die Grundlage der Spindynamik ist die Präzession eines magnetischen Moments unter dem Einfluss eines effektiven magnetischen Feldes Heff um die Feldachse. Dies wird durch die Bewegungsgleichung der Magnetisierung, der Landau-Lifshitz-Gleichung, beschrieben, die erstmals
von Landau und Lifshitz im Jahr 1935 veröffentlicht wurde [22]. Sie soll im Folgenden halbklassich hergeleitet werden [23, 24]. Eine quantenmechanische Rechnung findet sich zum Beispiel
in [25,26]. Zunächst soll der ungedämpfte Fall behandelt werden und anschließend die von Gilbert
stammenden Modifikationen erläutert werden.
Das atomare, magnetische Moment µ und der Drehimpuls J sind über folgenden Beziehung miteinander verknüpft:
µ = γJ .
(2.21)
Dabei ist γ das gyromagnetischen Verhältnis
γ=
gµB
~
.
(2.22)
7
2.2 Spindynamik
Heff
Heff
M×(M×Heff)
-M×Heff
-M×Heff
M
M
(a)
(b)
Abbildung 2.1: Stehen Magnetisierung M und effektives Magnetfeld Heff nicht parallel zueinander, wirkt ein Drehmoment D. Dies bewirkt eine Präzession der Magnetisierung um die Feldachse (siehe (a)). Durch Einführung eines Dämpfungsterms kommt eine zusätzliche Vektorkomponente
M × M × Heff radial zur Feldachse hinzu (dargestellt in (b)). Dieser Dämpfungsterm bewirkt eine
allmähliche Ausrichtung der Magnetisierung in Richtung des effektiven Feldes Heff .
Hierbei bezeichnet g den Landé-Faktor, µB das Bohrsche Magneton und ~ =
h
2π
das reduzierte
Plancksche Wirkungsquantum. Auf ein magnetisches Moment µ wirkt in einem effektiven Magnetfeld Heff das Drehmoment D (siehe Abbildung 2.1)
D=
dJ
= µ × Heff
dt
.
(2.23)
Wenn man von atomaren magnetischen Momenten zur Magnetisierung übergeht und (2.21) verwendet, ergibt sich die Landau-Lifshitz-Gleichung:
dM
= −γ(M × Heff ) .
dt
(2.24)
Das effektive Feld Heff setzt sich aus allen Feldern (siehe Abschnitt 2.1), die an der Magnetisierung
angreifen, zusammen:
Heff = H0 + Hex + Hd + Hani + HM (t) + ...
.
(2.25)
Dabei ist H0 ein statisches und HM (t) ein dynamisches, von außen angelegtes Feld. Hd bezeichnet das Entmagnetisierungsfeld, welches von magnetischen Oberflächenladungen durch DipolDipol-Wechselwirkung erzeugt wird. Das Austauschfeld wird mit Hex bezeichnet, Hani fasst alle
durch die Kristallstruktur hervorgerufenen Anistropiebeiträge zusammen. Weitere Beiträge, wie
zum Beispiel die Magnetostriktion oder Austausch-Verschiebungseffekte (exchange bias) sollen
im Weiteren nicht berücksichtigt werden.
Die Landau-Lifshitz-Gleichung (2.24) beschreibt die Präzessionsbewegung der Magnetisierung
um die durch das effektive Magnetfeld Heff vorgegebene Achse. Aufgrund der fehlenden Dämpfung würde ein einmalig aus der Ruhelage ausgelenktes magnetisches Moment ewig weiter präze8
2.3 Spinwellen
dieren. Aus diesem Grund führten bereits Landau und Lifshitz einen phänomenologischen Dämpfungsterm der Form
αLL |γ|
M × (M × Heff )
(2.26)
Ms
ein [22]. Dabei bezeichnet αLL die Landau-Lifshitz-Dämpfungskonstante. Für den Grenzfall hoher
−
Dämpfung αLL ≫ 1 ergibt sich jedoch ein physikalisch nicht sinnvolles Verhalten: die Präzessionsfrequenz steigt mit steigender Dämpfung an [27, 28]. Ein verbesserter Ansatz von Gilbert [29], der
aber weiterhin rein phänomenologischer Art ist, führt zur Landau-Lifshitz und Gilbert-Gleichung
dM
αG
dM
= −γ(M × Heff ) +
)
(M ×
dt
Ms
dt
(2.27)
mit dem dimensionslosen Gilbert-Dämpfungsparamter αG . Bei der Landau-Lifshitz und GilbertGleichung hängt der Dämpfungsterm von der zeitlichen Änderung der Magnetisierung ab und
verhindert so ein ansteigen der Präzessionsfrequenz mit zunehmender Dämpfung.
2.3. Spinwellen
Als Spinwellen bezeichnet man die kollektive Anregung der Magnetisierung. Wie bei Gitterschwingungen, die im Quasiteilchenbild als Phononen bezeichnet werden, spricht man bei Spinwellen im Bild der zweiten Quantisierung von Magnonen. Spinwellen entstehen durch die Wechselwirkung zwischen magnetischen Momenten. Je nachdem, welche Spinwellen-Wellenlänge vorliegt, unterscheidet man zwischen dipoldominierten oder austauschdominierten Spinwellen.
Die Landau-Lifshitz und Gilbert-Gleichung beschreibt die Dynamik eines einzelnen Spins bzw.
in der Makrospinnäherung die Dynamik einer kohärente Präzession in einem homogen magnetisierten Medium über das gesamte Volumen. Letzteres gilt für Spinwellen mit einem gegen Null
gehenden Wellenvektor (λ → ∞). In diesem Fall sind alle Spins immer parallel ausgerichtet. Um
die Präzessionsfrequenz für Spinwellen mit endlicher Wellenlänge bestimmten zu können, muss
die Landau-Lifshitz und Gilbert-Gleichung unter der Berücksichtigung der Maxwell-Gleichungen
im magnetostatischen Limit (Gleichung (2.2) und Gleichung (2.3)) gelöst werden. Um die LandauLifshitz und Gilbert-Gleichung analytisch lösen zu können, muss sie zunächst linearisiert werden.
Dazu betrachtet man einen in z-Richtung magnetisierten, isotropen und unendlich ausgedehnten
Festkörper und zerlegt die Magnetisierung und das Magnetfeld in einen statischen und einen dynamischen Anteil:

mx eiωt
M = M0 + m(t) =  my eiωt 
M0

(2.28)
9
2.3 Spinwellen

hx eiωt
H = H0 + h(t) =  hy eiωt 
H0

.
(2.29)
Hierbei wird zur Vereinfachung eine harmonische Zeitabhängigkeit der Magnetisierung und des
magnetischen Feldes angenommen. Des Weiteren sollen die Amplituden der dynamischen Komponenten im Vergleich zu den statischen klein sein:
mx ,my ≪ M0 und hx ,hy ≪ H0
.
(2.30)
Die Landau-Lifshitz und Gilbert-Gleichung kann mit den Ansätzen (2.28) und (2.29) unter Berücksichtigung von (2.30) linearisiert werden. Als Lösung erhält man für die kohärente Präzessionsfrequenz die sogenannte Kittel-Formel [30]
ν=
γ p
(H0 + 4πMs )H0
2π
.
(2.31)
Die Kittel-Formel ist ein Spezialfall für k = 0 cm−1 und gibt die Spinwellenpräzessionsfrequenz
der einzelnen Spins an. Diese Frequenz wird auch als ferromagnetische Resonanz (FMR) Frequenz
bezeichnet.
Geht man zu endlichen Wellenlängen über, stehen nicht mehr alle Spins parallel zueinander. Wegen der Verkippung benachbarter Spins muss Austausch- und Dipolenergie aufgebracht werden.
Außerdem ist die dynamische Magnetisierung nun ortsabhängig. Unter der Voraussetzung (2.30)
und der Beibehaltung der harmonischen Zeitentwicklung kann die dyanmische Magnetisierung
m(R,t) in ebene Wellen entwickelt werden
m(R,t) =
X
mk (t)eikR
.
(2.32)
k
In der Landau-Lifshitz und Gilbert-Gleichung muss nun das Austauschfeld (2.20) berücksichtigt
werden:
Hex = λex ∇2 M = λex ∇2 [M0 + m(R,t)] = −λex k 2 m(R,t) .
(2.33)
Mit Gleichung (2.33) ergibt sich als Lösung der Landau-Lifshitz und Gilbert-Gleichung die HerringKittel-Formel [31]
γ
ν=
2π
q
(H0 + λex k 2 )(H0 + λex k 2 + 4πMs sin2 θk )
.
(2.34)
θk beschreibt den Winkel zwischen dem Wellenvektor und der statischen Magnetisierung. Im Vergleich zur Kittel-Formel (2.31) ist das effektive Magnetfeld H0 um den Austauschterm λex k 2
10
2.3 Spinwellen
erhöht. Die Spinwellendispersion wächst für große Wellenvektoren aufgrund dieses Austauschtermes quadratisch mit k 2 . Solche Spinwellen werden als austauschdominiert bezeichnet, während
Spinwellen mit kleinen Wellenvektoren als dipoldominiert oder magnetostatisch bezeichnet werden.
Die Herring-Kittel-Formel beschreibt, wie oben bereits erwähnt, das Spinwellenspektrum eines unendlich ausgedehnten Ferromagneten. Beim Übergang zu einer dünnen magnetischen Schicht muss
sie hinreichend verändert werden. Die Einschränkung in einer Dimension bewirkt eine Quantisierung in Richtung der Flächennormale. Durch Reflexion der Spinwellen an den Schichtoberflächen
bilden sich stehende Wellen (Perpendicular Standing Spin Waves, PSSW) aus, die senkrecht zur
Schicht stehen. Sie werden nach der Anzahl ihrer Knoten unterschieden. Im Folgenden werden
jedoch nur die homogene PSSW-Mode mit p = 0 behandelt. Außerdem muss beim Übergang zu
dünnen Schichten berücksichtigt werden, dass die dynamische Komponente der Magnetisierung an
der Schichtoberfläche magnetische Oberfächenladungen erzeugt, welche aufgrund der langreichweitigen Dipol-Dipol-Wechselwirkung (Kapitel 2.1.1) die Dispersionsrelation verändern. Diese
durch die Oberflächenladungen hervorgerufenen Effekte wirken sich über die gesamte Schichtdicke aus und beeinflussen vor allem die dipolaren Spinwellen im Bereich großer Wellenlängen,
wenn die Austauschwechselwirkung vernachlässigbar ist. Die Dispersionsrelation für die über die
Schichtdicke homogene Mode lautet [32]:
γ q
ν0 (k) =
(H0 + λex k 2 )(H0 + λex k 2 + 4πMs F00 (θ, kk d)) .
2π
(2.35)
Das Dipol-Dipol-Matrixelement F00 ist eine Funktion des Winkels θ zwischen der statischen Magnetisierung und der auf die Schichtebene projezierten Wellenvektorkomponenten kk
F00 = 1 + P00 [1 − P00 (k)]
4πMs
sin2 θk − P00 (k) cos2 θk
H + λex k 2
mit
P00 = 1 −
1 − e−kk d
kk d
.
(2.36)
(2.37)
Für lange Wellenlänge weisen Spinwellen dipolaren Charakter auf und haben für verschiedenen
Winkel θk ein unterschiedliches Dispersionsverhalten. Die Dispersionsrelation (2.35) ist in Abbildung 2.2 für einen YIG Film der Dicke 5 µm und einem Feld von H0 = 1850 Oe graphisch
dargestellt. Wie zu sehen, gibt es zwei voneinander getrennte Dispersionsmannigfaltigkeiten für
Oberflächen-Spinwellen (Magnetostatic Surface Spin Waves, MSSW) und Volumen-Spinwellen
(Backward Volume Magnetostatic Spin Waves, BVMSW). Es ist anzumerken, dass im Folgenden keine höheren PSSW Moden berücksichtigt werden. In [34] ist gezeigt, dass OberflächenSpinwellen nur in einem Frequenzbereich oberhalb des Volumen-Bandes existieren können. Des
Weiteren gibt es einen minimalen Winkel θkrit , unter dem keine Oberflächen-Spinwellen existieren
11
2.3 Spinwellen
Frequenz (GHz)
MSSW
BVMSW
-1
k^ (cm )
-1
k|| (cm )
Abbildung 2.2: Dipolare Spinwellendispersion für einen 5 µm dicken YIG-Film mit einer in der Filmebene liegenden Magnetisierung und einem Magnetfeld von H0 = 1850 Oe [33]. Wie zu sehen, sind
die Dispersionsflächen der Oberflächenspinwellen (MSSW) und der Volumenspinwellen (BVMSW)
voneinander getrennt. Das Oberflächenband muss in einem Frequenzbereich oberhalb des Volumenbandes liegen. Ab einem bestimmten Winkel θkrit existieren keine Oberflächenspinwellen mehr [34].
können. Der Vollständigkeit halber soll erwähnt werden, dass es für eine aus der Schicht herauszeigende Magnetisierung sogenannte Forward-Volumenmoden gibt. In der vorliegenden Arbeit
lag die Magnetisierung jedoch stets in der Filmebene. Daher wird nicht näher auf die ForwardVolumenmode eingegangen.
Im Folgenden soll auf den Einfluss des dynamischen Streufeldes auf die Richtung der Gruppengeschwindigkeit und damit auf die Ausbildung der verschiedenen Spinwellentypen eingegangen
werden. Liegt die statische Magnetisierung in der Filmebene, bilden sich keine Streufelder aus
(siehe Kapitel 2.1.1). Existieren jedoch Spinwellen im Film, so gibt es eine dynamische Magnetisierung m(t) und somit auch ein dynamisches Streufeld hs (t). Diese Streufelder werden von der
out-of-plane Komponente der dynamischen Magnetisierung erzeugt. In Abbildung 2.3 ist dieser
Effekt für die Sonderfälle kkH0 und für k⊥H0 veranschaulicht. Wird die Wellenlänge verringert, liegen die antiparalleln out-of-plane Komponenten der dynamische Magnetisierung näher
zusammen und das Streufeld wird kleiner. Es resultiert eine Verringerung der Energie zum Aufbau des Streufeldes. Aus diesem Grund nimmt bei Backward-Volumenmoden die Frequenz mit
12
2.3 Spinwellen
H0, M0
H0
M0
(a)
(b)
5
5
4
4
1
3
2
4
5
3
3
l
l
2
2
1
1
Abbildung 2.3: Streufelder der dynamischen Magnetisierung bei dipolaren Spinwellen. Die dynamische Komponente der Magnetisierung, die sich innerhalb einer Wellenlänge um 360 ° dreht, ist in
Rot gezeichnet. Die durch diese erzeugten Streufelder sind gestrichelt gezeichnet. (a) Oberflächenwellen mit k⊥H0 und (b) Volumenwellen mit kkH0 . Erläuterungen siehe Text.
zunehmendem Wellenvektor (kleinere Wellenlänge) ab. Die Dispersion ist monoton fallend. Bei
den Oberflächenwellen wird dieser Effekt durch einen anderen überkompensiert: Die antiparallele Stellung der dynamische in-plane Komponente erhöht die Dipolenergie. Diese Erhöhung ist
größer als die Energieabsenkung durch die Reduzierung des Streufeldes. In diesem Fall steigt die
Frequenz mit zunehmendem Wellenvektor an. Liegt der Wellenvektor in einem beliebigen Winkel
zum angelegten Feld, tritt eine Mischform beider Situationen ein.
Nachfolgend werden die Spezialfälle k⊥H0 , θk = 90 ° und für kkH0 , θk = 0 ° näher betrachtet.
2.3.1 Magnetostatische Oberflächenmoden
Damon und Eshbach [36] berechneten erstmals 1961 die Dispersionsrelation für den Fall einer
senkrecht zur Magnetisierung propagierenden Spinwelle, θk = 90 °. Es handelt sich hierbei um
die magnetostatische Oberfächenmode (Magnetostatic Surface Spin Wave, MSSW), die aus historischen Gründen oft als Damon-Eshbach-Mode bezeichnet wird. In Abbildung 2.4 ist am Beispiel
eines 5 µm dicken YIG-Films die Dispersionsrelation für die MSSW- und die BVMSW Mode
bis k = 2,5 · 105 cm−1 gezeigt. Es ist deutlich zu erkennen, dass die Damon-Eshbach-Mode für
k = 0 cm−1 bei der ferromagnetischen Resonanzfrequenz (2.31) startet und dann eine monoton
steigende Dispersion zeigt, bis sie in Sättigung übergeht. Für noch größere k Werte würde sich die
k 2 -Abhängigkeit der austauschdominierten Spinwellen bemerkbar machen. Unter Vernachlässi gung der Austauschwechselwirkung und magnetischer Anisotropien lautet die Dispersionsrelation
für magnetostatische Oberflächenmoden:
q
γ
νMSSW =
H0 (H0 + 4πMs ) + (2πMs )2 (1 − e−2kk d ) .
2π
(2.38)
13
2.3 Spinwellen
M
k
Frequenz (GHz)
fFMR
MSSW
M
k
BVMSW
Wellenvektor k (cm-1)
Abbildung 2.4: Dispersion von dipolaren Spinwellen für einen 5 µm dicken YIG-Film mit
H0 = 1800 Oe, 4πMs = 1750 Oe, γ = 2π · 2.82 · 106 rad/s
Oe . Aus [35].
Die Damon-Eshbach-Mode zeichnet sich durch zwei Eigenschaften aus. Ihre maximale Amplitude liegt an der Schichtoberfläche und fällt zum Inneren hin exponentiell ab, daher der Name
Oberflächenmode“. Die Abklinglänge liegt in der Größenordnung der Spinwellen-Wellenlänge.
”
Außerdem besitzt die MSSW-Mode eine Vorzugsrichtung des Umlaufsinns auf der Probenoberfläche [23].
2.3.2 Magnetostatische Backward-Volumenmoden
Spinwellen, die parallel zur Magentisierungsrichtung propagieren (θk = 0 °), heißen BackwardVolumenmoden (Backward Volume Magnetostatic Spin Wave, BVMSW). Im Gegensatz zu Oberflächenmoden hat die dynamische Magnetisierung bei Volumenmoden über die Schichtdicke ein
nahezu konstantes Profil. Die Dispersionsrelation beginnt wie die MSSW-Mode für k = 0 cm−1
bei der ferromagnetischen Resonanz, fällt dann aber monoton, das heißt die Frequenz sinkt mit
größer werdendem Wellenvektor. Dies ist in Abbildung 2.4 gut zu erkennen. Im Bereich der austauschdominierten Spinwellen bei noch größeren Wellenvektoren wächst die Dispersion quadratisch mit k. Im Bereich kleiner Wellenvektoren ist die Gruppengeschwindigkeit
∂ω
∂k
negativ und
steht antiparallel zur Phasengeschwindigkeit ωk . Aus diesem Grund nennt man diese Spinwellen
Backward“ Volumenmode. Für die Dispersionsrelation ergibt sich [20]:
”
s
γ
1 − e−kk d
νBVMSW =
) .
H0 (H0 + 4πMs
2π
kk d
(2.39)
14
2.4 Parametrische Prozesse
(a)
H
H
M
h
M
h
H
(b)
H
M
h
M
h
Abbildung 2.5: Veranschaulichung der erzwungenen Verstärkung durch ein zusätzliches Magnetfeld
h⊥H. (a) Wenn die Frequenz des Hinzuschaltens der Präzessionsfrequenz entspricht erfolgt eine
Verstärkung. (b) Ist die Frequenz verschieden, so resultiert aufeinander folgend eine Verstärkung und
eine Abschwächung.
2.4. Parametrische Prozesse
Als parametrischen Prozess bezeichnet man die Verstärkung einer Schwingung durch periodische
Änderung eines bestimmten Parameters des anzuregenden Systems mit der doppelten Eigenfrequenz. Als Beispiel sei eine Kinderschaukel genannt: das Kind streckt die Beine aus und zieht sie
im richtigen Zeitpunkt wieder an den Körper (das heißt verlängert und verkürzt die Pendellänge
periodisch mit doppelter Schaukelfrequenz) und pumpt so Energie in das System Schaukel.
2.4.1 Erzwungene Verstärkung
Im Folgenden wird die erzwungene Verstärkung durch ein zusätzliches schwächeres Magnetfeld,
welches senkrecht zur Präzessionsachse steht, erläutert. Geht man davon aus, dass das magnetische Moment µ anfangs parallel zum äußeren Magnetfeld H steht, so beginnt es um die Feldachse
zu präzessieren, sobald ein zusätzliches, viel schwächeres Magnetfeld h⊥H für ein kurzes Zeitintervall eingeschaltet wird. Schaltet man dieses Magnetfeld h periodisch mit der Präzessionsfrequenz ein und aus, so vergrößert sich der Präzessionswinkel (Abbildung 2.5 (a)). Ist die Frequenz von der Präzessionsfrequenz verschieden, so resultiert im Allgemeinen keine Verstärkung
(Abbildung 2.5 (b)).
15
2.4 Parametrische Prozesse
2.4.2 Parametrische Verstärkung
Bei der erzwungenen Verstärkung regt man das System mit seiner Eigenfrequenz an. Bei der parametrischen Verstärkung dagegen verwendet man im Allgemeinen die doppelte Eigenfrequenz des
Systems, wie später gezeigt wird. Zwei wesentlichen Arten von parametrischen Pumpprozessen
werden hier dargestellt: das transversale und das longitudinale Pumpen. Im Fall des transversalen
Pumpens steht das zusätzliche schwächere Magnetfeld h, wie bei der erzwungenen Verstärkung,
senkrecht zum ursprünglichen Magnetfeld H. Wird h für eine in Bezug auf die Präzessionsdauer
kurzes Zeitintervall eingeschaltet, so beginnt das magnetische Moment M um die Magnetfeldachse zu präzidieren. Im Gegensatz zum transversalen Pumpprozess steht das zusätzliche Magnetfeld
h beim longitudinalen Pumpen parallel zum Magnetfeld H. Daher wird dieser Prozess auch paralleles Pumpen genannt.
Transversales Pumpen
Regt man einen Ferromagneten resonant oder nicht resonant durch ein zum Magnetfeld transversal
stehendes Mikrowellenfeld (h⊥H) an, so treten ab einer kritischen Mikrowellenleistung Spinwelleninstabilitäten auf. Dabei unterschiedet man zwischen vorzeitiger Sättigung“ (premature satu”
ration of main resonance), welche bei resonanter Anregung der uniformen Mode (k = 0 cm−1 )
auftritt, und der zusätzlichen Resonanz“ (subsidiary resonance), die bei nicht resonanter Anre”
gung auftritt. Dies konnte theoretisch von H. Suhl Mitte der 1950er Jahre [37,38] als paramterische
Anregung von Spinwellen erklärt werden.
Im Folgenden soll nur kurz auf die der transversalen Anregung zugrundeliegenden Prozesse eingegangen werden, da in der vorliegenden Arbeit ausschließlich das parallele Pumpen verwendet
wurde.
Erste Suhl-Instabilität
Bei der ersten Suhl-Instabilität handelt es sich um einen 3-Magnonen-Splitting-Prozess, bei dem
ein Magnon der uniformen Mode unter Energie- und Impulserhaltung in zwei Magnonen der halben Frequenz und entgegengesetzten Wellenvektor k und −k zerfällt (siehe Abbildung 2.6 (a)).
Falls ωp /2 innerhalb des Spinwellenbandes liegt, findet dieser Prozess immer statt. Die angeregten
Magnonen müssen also die halbe Energie der uniformen Mode haben. Dies ist der Fall für
ωp
0 < H0 <
.
(2.40)
2γ
Ab einer ausreichend großen Mikrowellenleistung – einem kritischen Feld hkrit entsprechend –
werden mehr Spinwellen erzeugt als zur gleichen Zeit dissipiert werden und es kommt zu einem
exponentiellen Anstieg der Spinwellen: Die Instabilität tritt ein.
16
2.4 Parametrische Prozesse
wp
wp
wp
wp/2
-k
k
wp/2
-k
k
(a)
-k
k
(c)
(b)
Abbildung 2.6: Parametrische Prozesse. (a) Die erste Suhl Instabilität ist ein 3-Magnonen-SplittingProzess. (b) Die zweite Suhl Instabilität ist ein 4-Magnonen-Splitting-Prozess. (c) Dargestellt ist der
1-Photon-2-Magnonen-Prozess der Parallel-Pump Instabilität.
Zweite Suhl Instabilität
Die zweite Suhl Instabilität ist ein 4-Magnon-Splitting-Prozess (siehe Abbildung 2.6 (b)). Hierbei
zerfallen zwei Magnonen der uniformen Mode unter Energie- und Impulserhaltung in zwei Magnonen gleicher Frequenz und entgegengesetztem Wellenvektor k und −k. Dieser Prozess findet
ebenfalls immer statt, wenn ωp innerhalb des Spinwellenbandes liegt:
0 < H0 <
ωp
γ
.
(2.41)
Man kann die zweite Suhl Instabilität aber nur innerhalb des Feldbereichs
ωp
ωp
< H0 <
2γ
γ
(2.42)
beobachten, da für kleinere Magnetfelder die Schwelle für die erste Suhl Instabilität geringer ist.
Longitudinales oder paralleles Pumpen
Nicht nur bei transversaler, sondern auch bei paralleler Mikrowellenanregung kann eine Spinwelleninstabilität beobachtet werden. Schlömann und Morgenthaler entwickelten bereits 1960 ein
solches Paralleles Pump“-Experiment, bei dem Spinwellen direkt ohne Antreiben der uniformen
”
Mode angeregt werden. Dieser Prozess eignet sich daher besonders zur Untersuchung von Spinwellendämpfungen. Der zugrunde liegende Prozess ist ein 1-Photon-2-Magnonen-Prozess (Abbildung 2.6 (c)), der wie die erste Suhl Instabilität in einem Feldbereich
0 < H0 <
ωp
2γ
(2.43)
17
2.4 Parametrische Prozesse
wp
wp
wp
wp/2
wp/2
wp/2
k
-k
-k
k
k
hkrit (Oe)
-k
H0 (Oe)
Abbildung 2.7: Butterfly-Kurve. Unterhalb von H0 = 947 Oe werden Magnonenpaare bei k > 0 und
θk = 90 ° instabil, oberhalb bei k = 0 und θk < 90 °. Hier für den Fall einer YIG-Kugel; aus [41].
auftritt. Die kritische Feldstärke hkrit des treibenden Mikrowellenfeldes ist nach [39, 40] bestimmt
durch:
hkrit =
ωp · ∆Hk
γ4πMs · sin2 θk
.
(2.44)
min
Ausdruck (2.44) wird bezüglich aller k minimiert. ωp bezeichnet die Pumpfrequenz und ∆Hk ist
die Spinwellenlinienbreite. In Abbildung 2.7 ist die sogenannte Butterfly-Kurve dargestellt: Das
kritische Mikrowellenfeld hkrit ist gegen das äußere Magnetfeld H0 aufgetragen.
Das äußere Feld H0 , bei dem das Mikrowellenfeld hkrit minimal wird, heißt kritisches äußeres
Magnetfeld Hkrit . Hier werden Spinwellen mit k ≈ 0 cm−1 und θk = 90° angeregt. Für kleinere
Magnetfelder H0 < Hkrit werden Spinwellen mit k > 0 und θk = 90° angeregt. Die Schwelle hkrit
steigt aufgrund der Abhängigkeit von ∆Hk von k zu kleineren Feldern H0 < Hkrit hin an [42].
Bei höheren Feldern H0 > Hkrit werden Spinwellen mit k = 0 cm−1 und θk < 90 ° instabil.
Aufgrund des sin2 θk -Terms im Nenner von Ausdruck (2.44) steigt die Mikrowellenschwelle hkrit
für größere Felder H0 stark an.
Klassisch lässt sich der parametrische Pumpprozess nicht durch eine Präzession der Magnetisierung auf einem Kegel erklären. Wäre dies der Fall, würde sich, wie später gezeigt, die in das System
während einer Präzessionsdauer gesteckte Energie wegmitteln. Dabei gilt: M = mx + my + Mz .
Der Betrag dieses Ausdrucks ist wegen der starken Austauschwechselwirkung in einem Ferromagneten konstant. Des Weiteren gilt für eine rein zirkulare Präzession |mx |2 + |my |2 = const. und
18
2.4 Parametrische Prozesse
Frequenz (GHz)
(a)
(b)
H0
14
wp
12
Ms
10
M
8
wD=wp/2
a
6
h
-kD
4
-kBEC
-10
5
-10
4
k??H
3
-10 -102 -10
1
kD
kBEC
10
1
2
10
10
3
10
4
10
5
k (cm
-1
)
Abbildung 2.8: (a) Geht man von einer zirkularen zu einer ellipsoidalen Präzession über und existiert ein zusätzliches Magnetfeld h, tritt eine parametrische Verstärkung auf. Das hinzugeschaltete
Magnetfeld h oszilliert mit der doppelten Präzessionsfrequenz. (b) Darstellung des parametrischen
Pumpprozesses. Das Pump-Photon zerfällt in 2 Magnonen. Bei langem Pumpen dominiert nur eine
der unterschiedlichen Spinwellengruppen, die dominante Gruppe (in lila). Von dort relaxieren die
Magnonen zum Spinwellenspektrum-Minimum. Hier kann sich ein Bose-Einstein-Kondensat bilden.
damit |Mz | = const.. Wird nun ein schwaches Magnetfeld h(t) = h0 cos(2ω0 t) mit der doppelten
Präzessionsfrequenz 2ω0 parallel zur Magentisierung der Probe Mz angelegt, so verschwindet die
Energie, die in das System gesteckt wird während der Präzessionsdauer T0 :
Z T0
1
∆E ∝ h · m = hMz = h0 Mz
cos(2ω0 t) = 0 .
T0 0
(2.45)
Geht man von einer zirkularen zu einer ellipsoidalen Präzession, wie in Abbildung 2.8 gezeigt,
über, so ist die in das System gesteckte Engerie ungleich Null. Dies soll nachfolgend gezeigt werden. Bei der ellipsoidalen Präzession oszilliert auch die z-Komponente des magnetischen Moments
Mz um einen konstanten Wert Mz = const. + mz,0 cos(2ω0 t). Für die in das System transferierte
Energie gilt:
∆E ∝
Z
T0
cos2 (2ω0 t) 6= 0 .
(2.46)
0
Nachfolgend soll der in dieser Arbeit verwendete Parallel-Pump-Prozess anhand von Abbildung
2.8 näher erklärt werden. Ein Mikrowellenfeldphoton erzeugt unter Energie- und Impulserhaltung
in einer der möglichen Spinwellengruppen ein Paar aus zwei Magnonen. Aus der Homogenität des
Pumpfeldes folgt, dass die Magnonen eines Paares entgegengesetzten Wellenvektor besitzen. Aus
einem stationären Pumpen folgt die Energieerhaltung. Zusammen mit der Tatsache, dass das Spektrum symmetrisch ist, ergibt sich, dass die Frequenz der Magnonen gerade der halben Pumpfrequenz entspricht. Über das Pumpphoton sind die beiden Magnonen eines Paares in ihrer Phase
gekoppelt; daher kann die Gesamtheit der Magnonenpaare als Kondensat aufgefasst werden [43].
19
2.4 Parametrische Prozesse
Der Pumpprozess ist für die verschiedenen, möglichen Spinwellengruppen unterschiedlich effizient. Es kommt zu einer Verstärkung der Gruppe, wenn die Pumpstärke das entsprechende Verhältnis von Linienbreite ∆Hk zu Kopplungsstärke sin2 θk übersteigt (siehe Gleichung 2.44). Für langes
Pumpen setzt sich nur eine Gruppe durch, die als dominante Gruppe bezeichnet wird. Aufgrund
ihres internen Feldes setzt sie die effektiv wirkende Pumpstärke herab und verhindert so die effiziente Verstärkung anderer Gruppen [44].
Wie beschrieben, sind sind die Magnonen aufgrund des elektromagnetischen Pumpfeldes paarweise gekoppelt. Die Vier-Magnonenstreuung ist daher unterdrückt und der Energietransfer in andere
Teile des Spektrums somit stark eingeschränkt. Wenn das Pump-Feld ausgeschaltet wird und damit die Kopplung der Magnonenpaare ausfällt, kommt es zur Vier-Magnonenstreuung und einer
schnellen Thermalisierung der Energie zum Minimum des Spinwellenspektrums. Hier kann sich
ein Bose-Einstein-Kondensat von Magnonen bilden, was erstmals von S. O. Demokritov in Zusammenarbeit mit B. Hillebrands und Weiteren 2006 [13] beobachtet wurde.
20
KAPITEL 3
Experimenteller Aufbau
3.1. Yttrium-Eisen-Granat
In der vorliegenden Arbeit wurden Spinwellen in wenige µm dünnen Filmen aus Yttrium-EisenGranat (englisch: Yttrium-Iron-Garnet, kurz YIG, Y3 Fe5 O12 ) untersucht.
Abbildung 3.1: YIG Kristallstruktur [45]. YIG kristallisiert kubisch-raumzentriert und hat 160 Atome
je Elementarzelle. Fe3+ Ionen besetzen oktaedrische (grünlich schattiert) und tedraedrische (rötlich
schattiert) Gitterplätze, die entgegengesetzte magnetisiert sind. Die Y3+ Ionen sind dodekaedrisch
koordiniert.
Bei der Untersuchung von Spinwellen spielt YIG eine herausragende Rolle. Es besitzt die schmalste bekannte ferromagnetische Resonanz Linienbreite und damit die geringste Spinwellen-Dämpfung. YIG ist ein kubisch-raumzentrierter (bcc), ferrimagnetischer Isolator mit 8 Formeleinheiten
je Elementarzelle [46]. Die Raumgruppe von YIG ist Oh (10) – Ia3d. Y3+ ist diamagnetisch. Die
resultierende äußere Magnetisierung ergibt sich aus zwei entgegengesetzt magnetisierten Gittern
21
3.1 Yttrium-Eisen-Granat
YIG
Al
G
Su GG
bst
rat
um
ini
An
ten
ne
um
nit
rid
Masse
Su
bs
tra
t
Abbildung 3.2: Aufbau der Probe
Sättigungsmagnetisierung MS
gyromagnetisches Verhältnis γ
FMR Linienbreite
Gilbert Dämpfungsparameter α
1750 G
2π· 2.82· 106 rad/s
Oe
0.5 Oe
0.00056
Tabelle 3.1: Eigenschaften von YIG
aus Fe3+ Ionen (siehe Abbildung 3.1). Am absoluten Nullpunkt hat jedes Fe3+ Ion ein magnetisches Moment von 5 µB . Je Formeleinheit sitzen drei Fe3+ Ionen auf oktaedrischen Gitterplätzen sogenannten d Plätzen - und sind in eine Richtung magnetisiert. Die beiden anderen Fe3+ Ionen sitzen auf tedraedrischen - sogenannten a Plätzen - und sind entgegengesetzt magnetisiert [47]. Daher
erhält man eine Magnetisierung von ingesamt 5 µB pro Formeleinheit. Der Unterschied zwischen
den oktaedrischen und den tedraedrischen Gitterplätzen liegt in der unterschiedlichen Konfiguration von benachbarten O-Ionen, die für den Superaustausch [48] zwischen den magnetischen Ionen
verantwortlich sind [49].
Die Probe besteht aus einem Substrat aus Gallium-Gadolinium-Granat (GGG), auf dem auf beiden Seiten ein identischer YIG Film angebracht ist. Die über dem GGG liegende YIG Schicht ist
für die Experimente nicht wichtig und wird im Weiteren nicht berücksichtigt. Der Grund für die
beidseitige Beschichtung des Substrats liegt in der Herstellung mittels Flüssigkeitsphasen Epitaxie, bei der das YIG auf dem GGG aufwächst. Spinwellen werden in dem YIG Streifen detektiert,
der sich unter dem GGG Substrat befindet. Dies ist möglich, weil YIG und GGG transparent sind.
Die komplette Probe wurde auf einem Substrat aus Aluminiumnitrid befestigt. Dieses Material
zeichnet sich besonders durch seine thermischen Eigenschaften aus: Wegen seiner guten Wärmeleitfähigkeit sorgt es dafür, dass sich die Probe durch die Mikrowellen nicht übermäßig erhitzt.
Auf dem Aluminiumnitrid Substrat befindet sich eine 50 µm breiten Antenne; die Rückseite des
Substrats ist vollständig metallisiert und dient als Masse. Ein Schema des Probenaufbaus ist in
Abbildung 3.2 zu sehen.
22
3.2 Probenaufbau
UV Licht
nach dem Bedampfen:
5 nm Chrom
+ 500 nm Kupfer
AZ nLof
Substrat
Maske
AZ nLof
Substrat
nach dem Lift-offProzess:
nach der Entwickeln:
AZ nLof
Substrat
5 nm Chrom
+ 500 nm Kupfer
Substrat
Abbildung 3.3: Schematische Abfolge des Lift-off-Prozesses. Anfangs wird der Lack mit UV-Licht
belichtet und danach entwickelt. Anschließend wird das gewünschte Material (hier Chrom und Kupfer) aufgedampft. Nach dem Lift-off bleibt das Metall nur noch an den Stellen stehen, an denen nach
der Entwicklung kein Lack mehr verblieben ist. Als Substrat“ kam hier YIG zum Einsatz.
”
3.2. Probenaufbau
In diesem Kapitel wird lediglich der Aufbau der Proben, die in Kapitel 4.1.3 verwendet werden,
vorgestellt. Um die Charakteristik verschiedener Antennen zu untersuchen, wurden spezielle Proben angefertigt. In allen anderen Experimente wurde der YIG Film auf der Antenne fixiert. Im
Gegensatz dazu wurde hier die Antenne direkt auf das YIG prozessiert. Da YIG Film und Antenne
so in direktem Kontakt zueinander sind, ist die Anregung wesentlich effizienter. Bei der hier hergestellten Antenne handelt es sich um kurzgeschlossene coplanar striplines, wie in Abbildung 3.4 (a)
skizziert. In Kapitel 4.1.3 wird gezeigt, dass an unterschiedlichen Positionen auf dem YIG Streifen
aufgrund unterschiedlicher Abstände der Leiter der coplanar striplines, verschiedene SpinwellenWellenlängen angeregt werden. Man kann die verschiedenen Positionen also als unterschiedliche
Antennen auffassen.
Die coplanar striplines wurden mittels UV-Photolithographie und anschließendem Lift-off-Prozess
auf den YIG Film prozessiert (siehe Abbildung 3.3). Dabei wurde zunächst der Fotolack AZ nLof
2035 der Firma MicroChemicals [50] auf das YIG aufgetragen. Anschließend wurde der Lack
mit UV-Licht belichtet. Um die gewünschte Struktur zu erhalten, wurde eine Maske verwendet.
Durch die Belichtung werden die chemische Eigenschaften des Lacks verändert, so dass mit Hilfe
des Entwicklers AZ 726 MIF von MicroChemicals [50] der Lack nur von den nicht belichteten
Flächen entfernt wird. In Abbildung 3.4 (b) ist eine 100-fache Vergrößerung des entwickelten
Lacks zu sehen. In einem nächsten Arbeitsschritt wurden 5 nm Chrom und weitere 500 nm Kupfer
auf die Proben gedampft. Die dünne Chromschicht dient dabei lediglich als Haftvermittler. Anschließend wurden in einem Lift-off-Prozess die verbliebenen mit Chrom und Kupfer beschich-
23
3.3 Mikrowellenaufbau
(a)
(c)
(b)
5.99 mm
4.03 mm
49.25 mm
4.24 mm
5.98 mm
5.98 mm
49.26 mm
Kurzschluss
Abbildung 3.4: (a) Skizze der hergestellten Antenne. (b) Mikroskopaufnahme der Proben nach der
Entwicklung bei 100-facher Vergrößerung. (c) Mikroskopaufnahme der fertigen Antenne (100-fache
Vergrößerung). Die äußeren Leiter spielen in den hier präsentierten Experimenten keine Rolle.
teten Lackflächen entfernt, so dass lediglich die Antenne stehen blieb. In Abbildung 3.4 (c) ist
eine Vergrößerung der fertigen Antenne gezeigt. Die äußeren Leiter, die auf dem Foto zu sehen
sind, spielen für die in dieser Arbeit vorgestellten Experimente keine Rolle. Sie sollen in einem
zukünftigen Experiment verwendet werden. Des Weiteren sind auf den Bildern die noch nicht
kurzgeschlossenen striplines zu sehen. Der Kurzschluss wurde durch einen winzigen Tropfen Silberkleber hergestellt. Die Prozessierung der Proben erfolgte in Zusammenarbeit mit T. Brächer
und P. Pirro im Nano+Bio Center Kaiserslautern [51].
3.3. Mikrowellenaufbau
In dieser Arbeit wurden Spinwellen mittels Mikrowellen angeregt. Dabei regt das magnetische
Wechselfeld einer Mikrowellenantenne die magnetischen Momente in der Probe zur Präzession
an. Die Präzession erfolgt um die durch ein statisches Feld definierten Gleichgewichtslage. Die
Frequenz und die Amplitude der Spinwellen sind durch das Mikrowellensignal bestimmt. In Abbildung 3.5 ist das Oerstedfeld einer Microstrip-Antenne mit einer Querschnittsfläche von 50 µm
× 5 µm dargestellt. Die x-Komponente des Magnetfelds erstreckt sich im Wesentlichen über die
Breite der Antenne. Umgekehrt kann das von der Spinwelle erzeugte Magnetfeld in der Mikrowellenantenne eine hochfrequente Wechselspannung erzeugen und die Spinwelle ist somit detektierbar. Spinwellen propagieren gemäß der Abstrahlcharakteristik bevorzugt senkrecht zur Antenne.
Für die Untersuchung der direkten Anregung wird ein cw-Mikrowellensignal verwendet, wohingegen bei der parametrischen Verstärkung gepulste Spinwellen benötigt werden, um trotz hoher
Leistungen ein Überhitzen der Probe zu vermeiden. Dabei müssen aus dem cw-Signal der Mikrowellenquelle kurze, zeitlich scharf begrenzte Pulse erzeugt werden. Des Weiteren soll es bei
24
3.3 Mikrowellenaufbau
Feldstärke (Oe)
Magnetfeld an
der Oberfläche
x
Hx: rot
Hy: blau
Schnitt entlang der
Oberfläche
x (mm)
Abbildung 3.5: Oerstedfeld einer Microstrip-Antenne mit einer Querschnittsfläche von 50 µm × 5 µm.
Die x-Komponente des Magnetfelds fällt am Rand der Antenne sehr schnell auf nahezu Null ab.
der Untersuchung der parametrischen Verstärkung möglich sein, die Spinwellen nicht nur optisch
mittels BLS zu beobachten, sondern auch mithilfe eines Detektors auf einem Oszilloskop.
Eine detaillierte Übersicht über Mikrowellentechnik findet sich beispielsweise in [52, 53]. Nachfolgend sollen die verwendeten Schaltungen näher beschrieben werden.
3.3.1 Direkte Anregung von Spinwellen
Die Mikrowellenquelle liefert ein kontinuierliches Ausgangssignal variabler Frequenz zwischen 2
und 18 GHz und einer Leistung bis zu 13 dBm, was 20 mW entspricht. Da zur direkten Anregung
von Spinwellen keine weiteren Mikrowellenbauteile benötigt werden, kann die Mikrowellenquelle
direkt an die Antenne angeschlossen werden (Abbildung 3.6 (a)). Für die direkte Anregung wurde ein Ausgangssignal von 4 dBm (=2,5
b
mW) gewählt. Der Mikrowellengenerator wird mit der
Frequenz betrieben, die in der Nähe der mittels Netzwerkanalysator bestimmten ferromagnetische
Resonanzfrequenz (k = 0 cm−1 ) der verwendeten Probe liegt. Der Netzwerkanalysator funktio-
niert folgendermaßen: Das durch die Mikrowellen erzeugte dynamische Magnetfeld regt, wie oben
beschrieben, die magnetischen Momente in der Probe zur Präzession an. Misst man die Absorption
des Mikrowellensignals als Funktion der Frequenz, ist die Resonanzfrequenz eines magnetischen
Systems die Frequenz, bei der die Absorption maximal ist.
25
3.3 Mikrowellenaufbau
Puls
Pumpende
Mikrowellenquelle
Abschwächer
Stub
tuner
(a) Direkte Anregung
YZirkulator
50 W
Switch
Pumpende
Mikrowellenquelle
Verstärker
Verstärker
Abschwächer
Detektor
Oszilloskop
(b) Parametrische Verstärkung
Abbildung 3.6: Mikrowellenaufbau: (a) Bei der direkten Anregung von Spinwellen wird die pumpende Mikrowellenquelle direkt mit der Antenne verbunden. (b) Um Spinwellen paramterisch zu
verstärken wird das Mikrowellensignal gepulst und anschließend verstärkt. Mit Hilfe des Oszilloskops läßt sich das von der Probe reflektierte Signal darstellen.
3.3.2 Parametrische Verstärkung
Bei der Untersuchung der parametrischen Verstärkung wird das Mikrowellen-Pumpsignal zunächst
verstärkt. Ein schneller Schalter, der von einem Pulsgenerator gesteuert wird, erzeugt aus dem
kontinuierlichen Wellensignal einen Mikrowellen-Rechteckpuls mit einer Breite von einigen Nanosekunden und einer Periodizität in derselben Größenordnung. Außerdem wird der Pulsgenerator
zur Synchronisation des Oszilloskops und zur Zeitauflösung (Kapitel 3.5.1) des optischen Aufbaus
verwendet. Anschließend passieren die Pulse einen Abschwächer, mit dem es möglich ist, die Mikrowellenintensität und somit die Spinwellenintensität zu kontrollieren. Der Stub Tuner“ dient
”
zur Impendanzanpassung der Antenne. Durch Längenänderung eines Resonators kann eine Resonanzbedingung erfüllt werden. Über einen Y-Zirkulator wird das von der Probe reflektierte Signal
über einen Verstärker und einen Abschwächer zu einem Mikrowellendetektor geleitet. Um das
schwache, reflektierte Signal überhaupt detektieren zu können muss es verstärkt werden. Der zum
Verstärker in Serie geschaltete Abschwächer dient zur Anpassung der Signalstärke. Der Detektor wandelt anschließend das Mikrowellensignal in eine Spannung um, die dann vom Oszilloskop
dargestellt werden kann. Zum Schutz des Detektors wird ein Gleichstrom-Blocker zwischengeschaltet. Der Aufbau ist in Abbildung 3.6 (b) schematisch dargestellt.
26
3.4 Frequenzmessung mittels Interferometrie
3.4. Frequenzmessung mittels Interferometrie
3.4.1 Fabry-Perot-Interferometer
Die Funktionsweise eines Fabry-Perot-Interferometers (FPI) basiert auf der Vielstrahlinterferenz
an planparallelen Schichten [54]. Meist ist dies durch zwei hochreflektierende Spiegel realisiert,
deren reflektierende Seiten sich im Abstand d gegenüberstehen. Des Weiteren ist die Rückseite
üblicherweise mit einer Antireflexionsschicht versehen, um die Effizienz zu erhöhen.
Abbildung 3.7 zeigt den schematischen Aufbau eines FPIs.
d
hochreflektierende
Schichten
Abbildung 3.7: Schematischer Aufbau eines Fabry-Perot-Interferometers.
Die Transmissionsfunktion ist durch
T = T0 ·
1
1 + F sin2 (∆φ/2)
(3.1)
gegeben [55,56]. Dabei bezeichnet F die Finesse des Etalons. Sie kann aus der Spiegelreflektivität
R bestimmt werden
F =
4R
(1 − R)2
(3.2)
und ist ein Maß für den Kontrast des Etalons. Die Transmissionsfunktion (3.1) ist periodisch mit
der Phasendifferenz ∆φ der interferierenden Teilstrahlen und wird maximal für ∆φ = 2mπ mit
m ∈ N. Bei festem Spiegelabstand d ist der Wegunterschied ∆s der am zweiten Spiegel interferierenden Teilstrahlen gegeben durch
∆s = 2nd
(3.3)
mit dem Brechungsindex n des Mediums zwischen den Spiegeln. Die Phasendifferenz ist bestimmt
durch
∆φ =
2π∆s
2nd
=
λ
λ
.
(3.4)
27
3.4 Frequenzmessung mittels Interferometrie
L·cos(a)
FP 2
FP 2
Scan-Richtung
a
FP 1
Scanbühne
Transmission
Umlenkspiegel
FP 1
TFPI
L Tandem-Fabry-PerotInterferometer
(a) Aufbau
Referenzsignal
magnonisches
Signal
Spiegelposition
(b) Funktionsweise
Abbildung 3.8: Tandem-Fabry-Perot-Interferometer [35]: (a) Vergrößerter Ausschnitt des TandemFabry-Perot-Interferometers. (b) Skizziert ist die transmittierte Intensität gegen den Spiegelabstand
sowohl für beide Etalons (FP 1 und FP 2), als auch für das Tandem-Fabry-Perot-Interferometer
(TFPI). Die höheren Ordnungen verschwinden beim TFPI nicht vollsttändig, da die GesamtTransmissionsfunktion nicht auf Null abfällt.
Mit der Bedingung ∆φ = 2mπ mit m ∈ N folgt, dass bei variablem Spiegelabstand d die Transmission für d = mλ/2 maximal wird. Für festen Spiegelabstand bezeichnet man ein Fabry-PerotInterferometer als Etalon. Man bezeichnet den von zwei Transmissionsmaxima eingegrenzten Frequenzbereich als freien Spektralbereich und kürzt ihn üblicherweise mit FSR (Free Spectral Range)
ab.
3.4.2 Tandem-Fabry-Perot-Interferometer
Wegen der Periodizität der Transmissionsfunktion (3.1) des Fabry-Perot-Interferometers wiederholt sich das gemessene Spektrum in Abständen des freien Spektralbereichs. Es ist daher möglich,
dass sich Stokes- und anti-Stokes-Spektren verschiedener Ordnung überlagern. Um eine eindeutige Frequenzzuordnung zu gewährleisten und um einen hohen Kontrast zu erreichen, kommt in
der vorliegenden Arbeit ein von J. R. Sandercock [57, 58] entwickeltes Multi-Pass Tandem-FabryPerot-Interferometer zum Einsatz. Es zeichnet sich durch einen Kontrast von mehr als 1 : 1010
sowie einer Auflösung im Sub-GHz-Bereich aus. Es besteht aus zwei in Serie geschalteten FabryPerot-Spiegelpaaren, deren optische Achsen um einen Winkel α gegeneinander verkippt sind. In
Abbildung 3.8 (a) ist der Aufbau skizziert.
Wie in Abbildung 3.9 gezeigt, gelangt das inelastisch gestreute Licht über ein Shuttersystem in
das Interferometer. Die Verwendung dieses Shuttersystems ist dringend notwendig: Für die Detektion der Photonen wird ein Photomultiplier mit sehr hoher Quantenausbeute verwendet. Das von
28
3.4 Frequenzmessung mittels Interferometrie
Spektralfilter
Räumlicher
Filter
Photodetekor
Shutter
System
Scanbühne
von der Probe
Referenzstrahl
Abbildung 3.9: Aufbau des Tandem-Fabry-Perot-Interferometers. Erläuterungen siehe Text.
der Probe elastisch gestreute, intensive Licht würde aufgrund der hohen Intensität den Photomultiplier zerstören. Andererseits ist die Messung der Referenzfrequenz des elastisch gestreuten Lichts
für die Bestimmung der Frequenz sowie zur Stabilisierung des Interferometers unabdingbar. Das
Shuttersystem sorgt nun dafür, dass abwechselnd das an Magnonen inelastisch gestreute Licht oder
ein geringer Teil des vorher ausgekoppelten Referenzlichts in das Interferometer gelangt. Da das
Interferometer nur über den Referenzstrahl stabilisiert wird, ist die Stabilisierung unabhängig von
der zu untersuchenden Probe.
Anschließend gelangt der Laserstrahl über einen Umlenkspiegel und einige räumliche Filter auf
das erste Etalon, dessen linke Seite starr mit dem Tisch verbunden ist, während die rechte Seite
auf einer piezoelektrischen Scanbühne montiert ist. Falls der Spiegelabstand d ein ganzzahliges
Vielfaches der halben Wellenlänge λ ist - also das Licht die Resonanzbedingung erfüllt - transmittiert das erste Etalon. Das Licht gelangt über einen weiteren Umlenkspiegel auf das zweite Etalon,
das in einem festen Winkel α gegenüber dem ersten montiert ist. Wiederum ist die rechte Seite
des Etalons auf der gemeinsamen Scanbühne befestigt. Der linke Spiegel ist fest auf dem Tisch
montiert.
Die Scanbühne dient dazu die Spiegelabstände zu variieren und so ein Spektrum aufzuzeichnen.
Erfüllt das zweite Etalon ebenfalls die Resonanzbedingung, kann das Licht passieren. Um einen besonders hohen Kontrast zu erzielen, durchläuft das Licht beide Etalons insgesamt drei mal (Abbildung 3.9), bevor es schließlich mit Hilfe eines Photomultipliers detektiert wird. Man spricht daher
von einem (3+3) Tandem-Fabry-Perot-Interferometer. Das gesamte Interferometer ist zusätzlich
auf einer Stabilisierungsbühne gelagert. Die Steuerung, Stabilisierung und Erfassung des Signals
wurde mit dem von H. Schulheiß entwickelten Programm TFPDAS4 (Tandem-Fabry-Perot-Data-
29
3.5 Brillouin-Lichtstreuspektroskopie
(a) ws=wi-w
ks=ki-k
w, k
w, k
wi, ki
Erzeugung (Stokes)
wi
(b)
ws=wi+w
ks=ki+k
wi+w
wi-w
wi , k i
Vernichtung (Anti-Stokes)
Frequenz
Abbildung 3.10: Brillouin-Lichtstreuspektroskopie. (a) Schematische Darstellung einer PhotonMagnon-Streuung. Es kann sowohl ein Magnon erzeugt als auch vernichtet werden. Das gestreute
Photon verliert oder gewinnt dabei Energie und Impuls. ωi und ki bezeichnen Frequenz und Wellenvektor des einfallenden Photons; ωs und ks beschreiben das gestreute Photon und ω und k das
Magnon. (b) Typisches BLS Spektrum.
Aquisation-Software) durchgeführt. Es ist eine mit dem Programmiersystem LabView erstellten
Weiterentwicklung der von B. Hillebrands geschriebenen TFPDAS3 Software.
Verfährt man die piezoelektrische Scanbühne um die Strecke L, ändert sich der Spiegelabstand
des ersten Etalons ebenfalls um L, der des zweiten Etalons lediglich um L · cos α. Soll nun das
Licht von beiden Etalons transmittiert werden, muss die Bedingung (3.1) simultan für beide Spiegelabstände erfüllt werden. Wie in Abbildung 3.8 (b) gezeigt sind Etalon eins und Etalon zwei
für die zentrale Ordnung gleichzeitig in Transmission. Die höheren Ordnungen werden vom zweiten Etalon jedoch bei einem anderen Spiegelabstand transmittiert als vom ersten Etalon. Da die
Gesamttransmissionsfunktion durch das Produkt der einzelnen Transmissionsfunktionen gegeben
ist, werden die höheren Ordnungen stark unterdrückt und nur die zentrale Ordnung wird maximal
transmittiert. Dies stellt die eindeutige Frequenzzuordnung sicher.
3.5. Brillouin-Lichtstreuspektroskopie
Die Brillouin-Lichtstreuspektroskopie (BLS) stellt seit den 1970er Jahren eine versierte Methode
zur Untersuchung sowohl magnonischer als auch phononischer Anregungen in Festkörpern dar.
Anders als bei der Detektion von Spinwellen durch eine Mikrowellenantenne, bei der die Welle
nur über die gesamte Länge und am Ort der Antenne registriert wird, bietet die BLS eine Nachweismöglichkeit in jedem beliebigen Punkt auf der Probenoberfläche. Außerdem ist die Detektion
kurzer Wellenlängen mittels BLS möglich. Dies ist mit Mikrowellenantennen jedoch schwierig,
da die Breite der Antenne kleiner als die Spinwellen-Wellenlänge sein müsste und solch schmale
Antennen schwer herzustellen sind. Die BLS beruht auf der inelastischen Streuung von Photonen
mit Magnonen, welche die Quanten der magnetischen Anregung darstellen. Im Bild der Quasi-
30
no
k
M
ag
M
k
ag
q
ks
q
no
n
n
3.5 Brillouin-Lichtstreuspektroskopie
ki
ki
al
et
m
(b)
lis
ie
rt
eP
la
tte
Pr
ob
e
Pr
ob
e
q
ks
(a)
Abbildung 3.11: Typische BLS Streugeometrien: (a) Streuung in Vorwärtsrichtung, (b) Rückwärtsstreugeometrie.
Teilchen kann bei einem solchen Streuprozess entweder ein Magnon erzeugt (Stokes-Prozess) oder
vernichtet (Anti-Stokes-Prozess) werden. Dies ist in Abbildung (3.10) verdeutlicht.
Setzt man die Translationsinvarianz und die Zeitinvarianz des untersuchten Systems voraus, erhöhen
sich aufgrund der Impuls- und Energieerhaltung beim Anti-Stokes-Prozess (Vernichtung) die Frequenz und der Wellenvektor des gestreuten Photons. Umgekehrt verringern sich Frequenz und
Wellenvektor beim Stokes-Prozess (Erzeugung).
~ωs = ~ωi ± ~ω
(3.5)
~ks = ~ki ± ~k
(3.6)
Dabei bezeichnen ~ωi , ~ωs , ~ω und ~ki , ~ks , ~k die Energien und die Impulse des einfallenden
Photons, des gestreuten Photons und des erzeugten (-) bzw. des vernichteten (+) Magnons. Im
klassischen Bild kann man den Streuprozess als Bragg-Streuung interpretieren, bei der das Licht
an einem sich bewegenden Phasengitter gestreut wird. Durch die dynamische Magnetisierung wird
die Permeabilität des Mediums moduliert und damit entsteht eine dynamische Modulation der Polarisation. Folglich wird die Wechselwirkung zwischen Photon und Medium moduliert: Es entsteht
ein Phasengitter, an dem das Licht gestreut wird. Die Frequenz des gestreuten Lichtes ist durch den
Dopplereffekt verschoben:
ωi = ωs − k · v
(3.7)
v bezeichnet dabei die Phasengeschwindigkeit der Spinwelle im Medium mit
v = (ω/k 2 ) · k
.
(3.8)
G = k = ki − ks
(3.9)
Zusammen mit der Bragg-Bedingung
31
3.5 Brillouin-Lichtstreuspektroskopie
Magnet
Umlenkspiegel
Probe
zum
Interferometer
Linse
Laser
Abbildung 3.12: Experimentelle Realisierung der Rückstreugeometrie.
und der Tatsache, dass der reziproke Gittervektor G gerade dem Wellenvektor k der Spinwelle
entspricht, ergeben sich wieder Gleichungen (3.5) und (3.6).
Aufgrund der Energieerhaltung (3.5) kann die Frequenz eines Magnons als Funktion der Frequenzverschiebung des gestreuten Lichts bestimmt werden. Nach der Bragg-Bedingung (3.9) entspricht
der maximal übertragene Wellenvektor dem doppelten Wellenvektor des einfallenden Photons. Die
Phasengeschwindigkeit der Magnonen kann im Vergleich zur Lichtgeschwindigkeit als sehr klein
angenommen werden. Daher ist die zu erwartende Frequenzverschiebung - bei gleichem Wellenvektor von Magnon und Photon - sehr klein
ωMagnon = vMagnon · k ≪ c · k ⇒ ωLicht − ωMagnon ≈ ωLicht
(3.10)
und liegt typischerweise im GHz Bereich. Um diese Frequenzbereiche mittels Brillouin-Lichtstreuspektroskopie detektieren zu können, kommt ein frequenzstabilisierter Festkörper-Laser als
Lichtquelle, sowie ein Tandem-Fabry-Perot-Interferometer (Kapitel 3.4.2) zur Frequenzselektion
zum Einsatz [56, 59].
Neben der Frequenz der Spinwelle ist der Wellenvektor eine direkt messbare Größe. In der vorliegenden Arbeit spielt die wellenvektoraufgelöster Brillouin-Lichtstreuspektroskopie eine zentrale
Rolle. Zur Messung wird ein neuartiger Aufbau verwendet, der in Kapitel 3.5.2 näher beschrieben ist. Da die Translationssymmetrie senkrecht zur Filmebene bei Streuung an dünnen Filmen
gebrochen ist, ist die Impulserhaltung (3.6) für die senkrechte Komponente des Wellenvektors
nicht mehr gültig. Für die parallel zur Filmebene liegende Komponente kk ist die Impulserhaltung weiterhin erfüllt. In dieser Arbeit wird ausschließlich in Rückstreugeometrie gemessen. Die
experimentelle Realisierung ist in Abbildung 3.12 dargestellt. Bei der Rückstreugeometrie liegen
32
3.5 Brillouin-Lichtstreuspektroskopie
BLS Intensität
Dt
Zeit
Frequenz Kanal
n1
n2 n3
t0
t0
t1 t2 t3
Frequenz
+
Ankunftszeit
Photon 1
00110100
0111011001000010010011
Photon 2
11110100
0011011001011010010010
Photon 3
10110100
0001011001000010010011
Abbildung 3.13: Zeitaufgelöste Brillouin-Lichtstreuspektroskopie: Die Frequenz und die Ankunftszeit jedes am Detektor auftreffenden Photons wird gleichzeitig gespeichert. Zur Aufnahme des
zeitaufgelösten Spektrums wurde die von H. Schultheiß und B. Obry entwickelte Software TFPDAS4TR verwendet.
einfallendes und gestreutes Licht parallel zueinander und es gilt ki = ks . Die untersuchte parallele
Wellenvektorkomponente kk ist gegeben durch
4π
kk =
· sin θ
λ
,
(3.11)
wobei λ die Wellenlänge des Laserlichts und θ den gegen die Schichtnormale gemessenen Einfallswinkel bezeichnet. Bei fester Wellenlänge λ = 532 nm kann durch Variation des Einfallswinkels θ
ein Wellenvektorbereich von kk = 0 bis 2,36 · 105 cm−1 untersucht werden.
3.5.1 Zeitaufgelöste Brillouin-Lichtstreuspektroskopie
Um Informationen über die Dynamik eines Systems zu erhalten, können zum einen Prozesse direkt
zeitaufgelöst beobachtet werden, zum anderen ist es möglich durch Messung im Frequenzraum und
anschließender Fouriertransformation zur selben Informationen zu gelangen. Um Messungen im
Zeitraum durchführen zu können, müssen die Zeitskalen der ablaufenden Prozesse aufgelöst werden können. Ist dies nicht der Fall, muss auf Messungen im Frequenzraum zurückgegriffen werden.
Die Spektroskopie, und damit auch die Brillouin-Lichtstreuspektroskopie, gehört zum klassischen
Fall einer Frequenzanalyse. Die zeitaufgelöste Brillouin-Lichtstreuspektroskopie verwendet man,
um langsame Spinwellen-Zerfallsprozesse beobachten zu können und um untersuchen zu können,
33
3.5 Brillouin-Lichtstreuspektroskopie
wie schnell die Energie einer Spinwellenmode in die veschiedenen Zerfallskanäle übergeht. Außerdem lässt sich damit die Spinwellenpropagation beobachten.
Zur Untersuchung von Spinwellenzerfällen mittels BLS muss die Zeitauflösung deutlich kleiner als
die Dauer des beobachteten Prozesses sein. Der Spinwellenzerfall geschieht innerhalb von Nanobis Mikrosekunden, weshalb die Zeitauflösung im Sub-Nanosekundenbereich liegen muss. Außerdem muss ein genau festlegbarer Zeitnullpunkt gesetzt werden können, um den Zeitpunkt eines
Ereignisses zu bestimmen. Da man nicht genau sagen kann, wann eine Spinwelle thermisch angeregt wurde, ist es aus diesem Grund auch nicht möglich, thermische Spinwellen zeitaufgelöst
zu messen. Folglich verwendet man Spinwellenpulse, deren Beginn als Zeitreferenz dienen kann.
Die einmalige Anregung eines Spinwellenpulses reicht nicht aus, um die ablaufenenden Prozesse
abbilden zu können. Erst die mehrmalige Wiederholung der immer gleich ablaufenden Prozesse
und anschliessende Summation liefert die zeitliche Intensitätsverteilung. Daher kann man bei der
zeitaufgelösten BLS auch von einem stroboskopischen Messverfahren sprechen.
Zur Zeitauflösung wird in dieser Arbeit ein P7887-PCI-PC Board der Firma FAST Com-Tec [60]
verwendet, welches als Flugzeit-Analysator fungiert. Mit Hilfe dieser Karte ist es möglich Zeitund Frequenzinformation gleichzeitig zu speichern und damit den Zerfall einer Eigenmode zeitaufgelöst in eine andere Eigenmode zu beobachten. Das Verfahren ist schematisch in Abbildung 3.13
gezeigt.
Derselbe Pulsgenerator, der den Mikrowellenschalter (siehe Kapitel 3.3) steuert, legt auch den
Startpunkt der Zeitmessung fest. Dazu wird das Trigger Out Signal des Pulsgenerators mit dem
P7887 Board verbunden und die Zeitauflösungskarte kann für eine durch die Software festgelegtes
Zeitintervall Ereignisse registrieren. Mit Hilfe der Delay-Funktion des Pulsgenerators ist eine Verschiebung des Zeitfensters der Messung möglich. Zur Aufnahme des zeitaufgelösten BLS Spektrums wurde die von H. Schultheiß und B. Obry entwickelte Software TFPDAS4-TR verwendet,
die näher in [61] beschrieben ist.
3.5.2 Wellenvektoraufgelöste Brillouin-Lichtstreuspektroskopie
In Abbildung 3.14 ist schematisch der Aufbau der in dieser Arbeit verwendeten BLS-Anlage gezeigt. Als Lichtquelle kommt ein frequenzverdoppelter, diodengepumpter Nd:YAG Laser vom Typ
Coherent Verdi V2 zum Einsatz. Dieser Dauerstrichlaser emittiert eine Wellenlänge von λ = 532 nm
und liefert einstellbare Leistungen von 10 bis 2000 mW. Ein Bruchteil des Laserlichts wird mit
einem Strahlteiler abgetrennt und dient als Referenzstrahl zu Stabilisierung des Interferometers,
sowie zur Messung der Referenzfrequenz (Frequenz des elastisch gestreuten Lichts). Der Rest des
linear polarisierten Laserlichts passiert zunächst ein λ/2-Element und gelangt anschließend auf
einen polarisierenden Strahlteilerwürfel. Mit dieser Kombination aus λ/2-Element und polarisie-
34
3.5 Brillouin-Lichtstreuspektroskopie
xyz-Verschiebetisch
Drehbarer Arm
Räumlicher
Filter
Spektralfilter
µw Quelle
Strahlteiler
Probenhalter
N
N
Lochblende
Photodetekor
Shutter
System
Scanbühne
Polarisationsfilter
Shunts
Referenzstrahl
S
S
Elektromagnet
motorisierter Rotator
l/2
Laser
Abbildung 3.14: Aufbau zur wellenvektoraufgelösten Brillouin-Lichtstreuspektroskopie: Links ist das
von C. Sandweg konzipierte sowohl horizontal als auch vertikal drehbare Joch zu sehen. Auf der
rechten Seite ist der übliche BLS-Aufbau gezeigt. Die einzelnen Komponenten werden im Text näher
erläutert.
rendem Strahlteiler ist es möglich, die Laserintensität auf der Probe zu regulieren. Das Laserlicht
wird mittels eines Objektivs auf die Probe fokussiert. Bei der Streuung erfährt das inelastisch gestreute Licht eine Drehung der Polarisationsebene um π/2. Ein Polarisationsfilter, der senkrecht
zur ursprünglichen Polarisationsrichtung steht, filtert das elastisch gestreute oder das an Phononen
gestreute Licht heraus. Des Weiteren sorgt eine zusätzliche Lochblende vor dem Polarisationsfilter
dafür, dass nur inelastisch gestreutes Licht von der Mitte des Objektivs detektiert wird, da sich dort
die Probe befindet. Anschließend fokussiert eine Linse das gestreute Licht auf die Eingangsblende
des Interferometers. Diese Blende dient dazu, Hintergrundlicht zu unterdrücken und unerwünschte Reflexe herauszufiltern. Direkt hinter der Blende befindet sich ein Shuttersystem, welches im
Kapitel 3.4.2 beschrieben wird.
Das Hauptaugenmerk der vorliegenden Arbeit liegt auf der wellenvektoraufgelösten BrillouinLichtstreuspektroskopie. Dabei wurde ein von C. Sandweg entwickeltes und realisiertes Konzept
verwendet. Zunächst soll aber kurz auf die bisher gängigen Verfahren zur wellenvektoraufgelösten
35
3.5 Brillouin-Lichtstreuspektroskopie
(a)
Probe
vom
Laser
zum
Interferometer
f
(c)
(b)
ks
f
ki
k
q
H
verschiedene Blenden
Abbildung 3.15: Erste wellenvektorabhängige Untersuchungen von Spinwellen wurden mit Blenden
verschiedener Öffnung realisiert [62, 63]. (a) Streugeometrie (b) Streugeometrie durch Wellenvektoren dargestellt: ki einfallendes Photon, ks gestreutes Photon, k Magnon. (c) Blende und Öffnung zur
Wellenvektorselektion. θ und φ werden im Text erläutert.
Detektion von Spinwellen eingegangen werden.
Ende der 1970er bzw. Anfang der 1980er Jahre wurden erste Anstrengungen unternommen, um
Spinwellen wellenvektoraufgelöst mittels BLS untersuchen zu können [62, 63]. Um den Wellenvektor präzise bestimmen zu können, verwendete man rotierbare oder horizontal und vertikal bewegbare Blenden mit unterschiedlichen Öffnungen (siehe Abbildung 3.15 (c)). Dabei ist der maximal erreichbare Wellenvektor kmax durch die Größe der Sammellinse hinter der Probe bestimmt.
Der Winkel φ kontrolliert die in-plane Komponente des Wellenvektors der streuenden Magnonen
(siehe Abbildung 3.15 (b)). Die Richtung des in-plane Wellenvektors in Bezug auf die Orientierung
des externen Magnetfelds ist durch die Position der Öffnung in der Blende bestimmt, wobei θ den
Winkel zwischen dem Magnon-Wellenvektor k und dem Feld H bezeichnet. Dies ist in Abbildung
3.15 (c) verdeutlicht. Mit dieser Technik sind Wellenvektoren bis k ≈ 4 · 104 cm−1 [64] detektierbar; daher eignet sich die Verwendung von Blenden nicht für die Untersuchung von Prozessen, die
bei größeren Wellenvektoren ablaufen (siehe Kapitel 4.2.2).
Außerdem gibt es die Möglichkeit, Spinwellenpakete phasenaufgelöst zu untersuchen und so aus
der Wellenlänge der Spinwelle den Wellenvektor zu ermitteln [15]. Mit diesem Verfahren sind
jedoch nur Wellenvektoren bis etwa k ≈ 250 − 300 cm−1 nachweisbar. Als Beispiel für diese Methode sind in Abbildung 3.16 (a) Ergebnisse von A. A. Serga et al. gezeigt. Als weitere Methode
Spinwellen wellenvektoraufgelöst zu beobachten sei ein von B. Hillebrands und S. O. Demokritov realisierte Aufbau genannt [65]. Dabei wurde die Probe zwischen den feststehenden Polen des
Magneten verkippt, wie in Abbildung 3.16 (b) gezeigt. Mit diesem Verfahren können für eine Wel-
36
3.5 Brillouin-Lichtstreuspektroskopie
(b)
(a)
7180
H =1831 Oe
Frequenz [GHz]
7160
α
7140
N
7120
S
H =1821 Oe
7100
7080
7060
0
50
1 00
150
200
250
300
Wellenvektor k [cm-1]
Abbildung 3.16: Weitere Methoden Spinwellen wellenvektoraufgelöst zu beobachten: (a) Durch phasenaufgelöste BLS lassen sich Rückschlüsse auf den Wellenvektor ziehen [15]. (b) Die Probe wird
zwischen den feststehenden Polschuhen des Magneten gedreht. Damit sind jedoch nur Spinwellen in
Damon-Eshbach Geometrie detektierbar [65].
lenlänge von λ = 532 nm Wellenvektoren bis |k| ≈ 2 · 105 cm−1 untersucht werden. Der große
Nachteil liegt darin, dass Spinwellen nur in Damon-Eshbach Geometrie, das heißt der Wellenvektor steht senkrecht zum angelegten Magnetfeld, untersucht werden können. Die Lösung dieses Problems besteht darin, ein Aufbau zu konstruieren, bei dem sowohl die Probe als auch die Polschuhe
des Magneten horizontal drehbar sind, also in der Erweiterung von einer auf zwei Dimensionen.
Dieser Weg wurde bei der hier verwendeten Apparatur eingeschlagen. In Abbildung 3.14 ist auf
der linken Seite der neuartige Aufbau zu sehen. Das komplette Joch mitsamt der Probe sitzt auf
einem motorisierten Rotator und lässt sich Software gestützt horizontal bewegen. Des Weiteren
ist der Probenhalter an einem drehbaren Arm befestigt, der sich ebenfalls mit Hilfe eines Rechners steuern lässt. Als Permanentmagnet kommen zwei NdFeB-Magnete zum Einsatz, die auf den
beiden Seiten des Jochs montiert wurden; das Joch an sich besteht aus speziell behandeltem Eisen ( VACOFER S1“), das sich durch seine besondere Reinheit und durch eine niedrige Koer”
zitivfeldstärke auszeichnet. Die Magnetpole sind so geformt, dass der Strahlengang des Lasers
nicht beeinflusst wird und die Homogenität des Magnetfeldes gewährleistet ist. Zusätzlich wurde ein Messingrahmen an das Joch angebracht, der zur Stabilisierung des Aufbaus dient und die
Möglichkeit bietet, eiserne Stangen ( shunts“) zu befestigen. Diese Eisenstangen dienen dazu, den
”
magnetischen Fluss zu variieren und so das Magnetfeld zwischen den Polen zu verändern. Für die
Feinregulierung des Magnetfeldes steht eine Spule zu Verfügung, die mit einem Strom von bis zu
5 A betrieben werden kann, was einer Magnetfeldänderung von etwa 300 Oe entspricht. Zusammen
mit einer Hallsonde wird so die Langzeitstabilität des Magnetfeldes sichergestellt.
Der Probenhalter ist auf einem xyz-Verschiebetisch montiert, welcher auf dem vertikal drehbaren
Arm sitzt. Der Winkel zwischen diesem Hebel und dem einfallenden Laserlicht lässt sich bis auf
37
3.5 Brillouin-Lichtstreuspektroskopie
∆θ = 0,1 ° genau bestimmen. Durch Variation des vertikalen Winkels kann die in-plane Komponente des Wellenvektors senkrecht zum angelegten Magnetfeld untersucht werden. Außerdem
können durch horizontale Drehung des Aufbaus Wellenvektoren parallel zum angelegten Magentfeld beobachtet werden, ohne die Magnetisierung der Probe zu verändern. Möglich wird dies
durch Positionierung des gesamten Aufbaus mitsamt des Magnetjochs auf einem Rotator, der sich
mit einer höheren Genauigkeit als ∆θ = 0,1 ° ansteuern lässt.
Mit dem hier vorgestellten Aufbau sind Wellenvektoren bis |k| ≈ 2,36 · 105 cm−1 nachweisbar.
Aufgrund des verwendeten Objektivs ist eine räumliche Auflösung von 25 µm gegeben. Wegen der
Heisenberg Unschärferelation beträgt die Wellenvektorauflösung etwa 3000 cm−1 . Des Weiteren
geht der Fehler aufgrund von Gleichung (3.11) mit cos(∆θ) ein und ist daher für kleinere Winkel
größer als für große Winkel.
38
KAPITEL 4
Experimentelle Ergebnisse und Diskussion
Wie bereits in Kapitel 3.5.2 beschrieben, wurden seit den 1970er Jahre verschiedene Aufbauten
und Methoden zur wellenvektorabhängigen Untersuchung von Spinwellen verwendet. Mit diesen Aufbauten war es entweder nur möglich, Spinwellen mit einem Wellenvektor von maximal
4 · 10−4 cm−1 zu detektieren oder lediglich Spinwellen, die senkrecht zum angelegten Magnetfeld
propagieren, zu vermessen. In Kapitel 4.1 wird zunächst anhand der Ergebnisse für die direkte Anregung von Spinwellen gezeigt, dass der hier vorgestellte Aufbau sowohl für den Fall von
parallel zum Magnetfeld propagierenden, als auch für den Fall von senkrecht zum Magnetfeld propagierenden Spinwellen verwendet werden kann. Der Aufbau ist also hervorragend für sämtliche
Mess-Geometrien in Rückwärtsstreuung geeignet und man kann damit dipolare Spinwellen langer
Wellenlänge messen. Im Anschluss daran werden verschiedene Antennen wellenvektorabhängig
charakterisiert. In Kapitel 4.2 werden die Ergebnisse vorgestellt, bei denen Spinwellen parametrisch verstärkt wurden. Dabei wurde sowohl das Minimum des Spinwellenspektrums als auch
die Gruppe mit der geringsten Dämpfung untersucht. Das Signal vom Minimum des Spinwellenspektrums wurde nicht nur wellenvektorabhängig, sondern auch zeitaufgelöst untersucht. Um
die optimale Mikrowellenleistung zu bestimmen, wurde das Signal der dominanten Gruppen leistungsabhängig aufgezeichnet. Des Weiteren wurde das Signal der dominanten Gruppe wellenvektorabhängig untersucht, um Rückschlüsse auf die Bildung eines Bose-Einstein-Kondensates (BEC,
Bose-Einstein-Condensation) ziehen zu können.
4.1. Direkte oder erzwungene Anregung
Zur direkten Anregung von Spinwellen wird eine 50 µm breite Microstrip-Antenne verwendet (siehe Kapitel 3.3.1), auf die ein 7 µm dicker YIG Streifen (Abmessungen: 16×3 mm2 ) fixiert wurde.
Antenne und YIG-Streifen werden zwischen den Polen des Jochs positioniert und anschließend die
Antenne über ein SMA-Kabel mit einem Netzwerkanalysator verbunden. Hiermit ist es möglich,
die ferromagnetische Resonanzfrequenz des YIG Streifens zu bestimmen: Der Netzwerkanalysator
erzeugt Mikrowellen verschiedener Frequenz und detektiert, bei welcher Frequenz eine resonan-
39
4.1 Direkte oder erzwungene Anregung
Abbildung 4.1: Im Fall der Backward-Volumenmode stehen Wellenvektor und Magnetisierung parallel zueinander. Die Anregungsfrequenz betrug 7,04 GHz bei einem Magnetfeld von 1755 Oe. (a)
Die BLS-Intensität ist gegen den Winkel aufgetragen. (b) Die BLS-Intensität ist gegen den Wellenvektor dargestellt. Die Breite, bei der das BLS-Signal auf die Hälfte abgefallen ist, beträgt in etwa
1700 cm−1 .
te Absorption auftritt. Eine Mikrowellenquelle, die so eingestellt wurde, dass sie eine Frequenz
knapp über oder knapp unter der so ermittelte Frequenz liegt, liefert, wird nun mit der Antenne
verbunden.
4.1.1 Backward-Volumenmoden
Wie bereits in Kapitel 2.3.2 erläutert, stehen im Fall der Backward-Volumenmode der Wellenvektor der Spinwelle und die Magnetisierungsrichtung parallel zueinander. Um diese Spinwellen
detektieren zu können, wird das Joch zusammen mit der Probe horizontal rotiert.
Die Anregungsfrequenz betrug 7,04 GHz bei einem Magnetfeld von 1755 Oe und lag somit knapp
unter der ferromagnetischen Resonanzfrequenz von νFMR = 7,07 GHz (Abbildung 4.1 (a)). Die
Anregungsfrequenz wurde knapp unter der FMR gewählt, damit Spinwellen des BVMSW-Bandes
mit einem Wellenvektor |k| ≈ 0 cm−1 angeregt werden. Mit Hilfe des Winkels zwischen einfallendem Laserlicht und der Schichtnormalen kann über die Relation (3.11) der Wellenvektor berechnet
werden (Abbildung 4.1 (b)).
Die experimentellen Resultate (Abbildung 4.1) zeigen den erwarteten Verlauf: Eine MicrostripAntenne sollte bei der verwendeten Frequenz theoretisch vor allem Spinwellen mit einem Wellenvektor von |k| ≈ 0 cm−1 anregen. Dieses Verhalten konnte experimentell bestätigt werden: Die
maximale BLS-Intensität wurde bei einem gegen Null gehenden Wellenvektor detektiert und fällt
für größere Wellenvektoren schnell ab.
40
4.1 Direkte oder erzwungene Anregung
(a)
(b)
Abbildung 4.2: Im Fall der Damon-Eshbach-Mode stehen Wellenvektor und Magnetisierung senkrecht zueinander. Die Anregungsfrequenz betrug 7,98 GHz bei einem Magnetfeld von 2030 Oe. (a)
Die BLS-Intensität ist gegen den Winkel aufgetragen. (b) Die BLS-Intensität ist gegen den Wellenvektor dargestellt. Die Breite, bei der das Signal auf die Hälfte abgefallen ist, beträgt in etwa 1700 cm−1 .
Die Breite, bei der das Signal auf die Hälfte abgefallen ist, liegt bei etwa 1700 cm−1 . Diese
Auflösung lässt sich durch die Unschärferelation erklären, da der Laserspot lediglich eine Größe
von 25 µm aufweist. Außerdem muss berücksichtigt werden, dass das Objektiv aus mehreren Linsen besteht und man selbst bei zentralem Strahlendurchgang nie davon ausgehen kann, dass sich
keine Linsenfehler bemerkbar machen.
4.1.2 Oberflächen- oder Damon-Eshbach- Moden
In Kapitel 2.3.1 wurde die Theorie der Oberflächen-Mode, welche auch als Damon-Eshbach-Mode
bezeichnet wird, eingeführt. Hier stehen Wellenvektor der Spinwelle und die Magnetisierungsrichtung senkrecht zueinander. Um die Oberflächenspinwellen nachweisen zu können, wird der
Hebelarm mit der Probe vertikal gedreht.
Hier lag die Anregungsfrequenz knapp über der ferromagnetischen Resonanzfrequenz von
νFMR = 7,96 GHz, bei 7,98 GHz und einem Magnetfeld von 2030 Oe. Die Anregungsfrequenz
wurde knapp über der FMR gewählt, damit Spinwellen des MSSW-Bandes mit einem Wellenvektor |k| ≈ 0 cm−1 angeregt werden. Die Ergebnisse sind in Abbildung 4.2 dargestellt. Wie im Falle
der Backward-Volumenmode beträgt die Breite, bei der das BLS-Signal auf die Hälfte abgefallen
ist, etwa 1700 cm−1 und zeigt den erwarteten Verlauf: Die maximale BLS-Intensität wurde bei
einem Wellenvektor |k| ≈ 0 cm−1 detektiert. Zu größeren Wellenvektoren fällt das Signal rasch
ab.
41
4.1 Direkte oder erzwungene Anregung
Die primäre Idee, einen Aufbau, wie den in dieser Arbeit vorgestellten, zu realisieren, war die Untersuchung von Spinwellen mit größerem Wellenvektor. Insbesondere die Detektion der BackwardVolumenmode, die mit den bisherigen Methoden nur bis zu einem Wellenvektor von 4 · 104 cm−1
untersucht werden konnte. Außerdem sollten mit ein und dem selben Aufbau sowohl BVMSWals auch MSSW-Spinwellen nachgewiesen werden können. Wie in Abbildung 4.1 und 4.2 zu sehen, bietet der hier verwendete Aufbau eine hervorragende Möglichkeit, dies zu bewerkstelligen.
Beide Arten von Spinwellen können detektiert werden und wie in Kapitel 4.2 präsentiert, stellt der
Aufbau das Mittel der Wahl bei der Untersuchung von Spinwellen mit höherem Wellenvektor dar.
4.1.3 Untersuchung der Charakteristik verschiedener Antennen
In Kapitel 3.2 wird der Probenaufbau bzw. die Antennenstruktur näher erläutert. Im Unterschied
zur direkten Anregung, bei der eine Microstrip-Antenne verwendet wird, handelt es sich hier um
eine kurzgeschlossene Antenne wie im Inset von Abbildung 4.3 (a) gezeigt. Des Weiteren ist die
Antenne direkt auf den YIG-Streifen prozessiert worden, um eine optimale Anregung zu erzielen.
In diesem Kapitel sollen die Ergebnisse, die mit den eigens für diesen Zweck angefertigten Proben gemessen wurden, diskutiert werden. Die nachfolgend präsentierten Ergebnissen wurden in
BVMSW-Geometrie gemessen.
Die in Abbildungt 4.3 (a) gezeigten Resultate wurden mit einer kurzgeschlossenen Antenne erzielt, wie sie rechts dargestellt ist. Die Anregungsfrequenz betrug 7,28 GHz bei einem Magnetfeld
von 1980 Oe. Um Spinwellen verschiedener Wellenlänge anzuregen, wurde der Laserspot auf verschiedenen Stellen zwischen den beiden Leitern fokussiert. In den verschiedenen Positionen ist
der Abstand der beiden Leiter unterschiedlich und es werden aufgrund verschiedener Randbedingungen unterschiedliche Spinwellen-Wellenlängen erzeugt. Die verschiedenen Positionen auf dem
Streifen lassen sich also als unterschiedliche Antennen auffassen. Die Leiter haben am Ende (Position 1) eine Breite von ungefähr 6 µm, der Abstand zwischen beiden Leitern beträgt etwa 4 µm. In
Position 2 beträgt die Breite der Leiter jeweils 100 µm und der Abstand beider Leiter 130 µm. Anhand der dargestellten Messungen ist eindeutig zu erkennen, dass an den verschiedenen Positionen
auf dem YIG Streifen verschiedene Spinwellengruppen angeregt werden.
Ein Winkel von einem Grad entspricht einem Wellenvektor von ungefähr 4200 cm−1 . Daher muss
das Joch, um die in Abbildung 4.3 (a) gezeigten Resultate zu messen, um lediglich 3 Grad rotiert
werden. Es ist experimentell also nicht einfach zu bestimmen, wo sich die Nullposition exakt befindet. Hier wurde folgender Weg beschritten: für die vorliegenden Dimensionen der Antenne kann
man eine homogene Stromverteilung annehmen, wie es in Abbildung 4.3 (b) dargestellt ist. Durch
Fouriertransformation der Stromverteilung der Antennen wurde anhand von Abbildung 4.3 (b) der
Wellenvektor (für Position 2) bestimmt, bei dem die Intensität maximal ist. Dieser liegt theore-
42
4.1 Direkte oder erzwungene Anregung
(a)
(b)
FFT der Position 1
FFT der Position 2
Stromverteilung:
+
Position 2
-
Position 1
Kurzschluss
Abbildung 4.3: Antennencharakteristiken (a) Experimentelle Ergebnisse: In Schwarz ist das BLSSignal der ersten Position dargestellt. In Rot ist das BLS-Signal der zweiten Antennenposition abgebildet. Die maximale Intensität ist für beide Fälle auf 100 normiert. (b) Fouriertransformation der
homogenen Stromverteilung für beide Antennenpositionen. Hier ist ebenfalls die maximale Intensität
auf 100 (a. u.) normiert.
tisch bei rund 150 cm−1 . Der experimentell bestimmte Wellenvektor von Position 2, bei dem das
BLS Signal maximal ist, wird nun mit diesem Wert identifiziert. Der Abstand der jeweils ersten
Maxima der Fouriertransformation von Position 1 und Position 2 (Abbildung 4.3 (b)) beträgt etwa 2500 cm−1 und stimmt damit gut mit dem Abstand der beiden gemessenen Peaks von rund
2400 cm−1 in Abbildung 4.3 (a) überein.
In Position 1 wurde eine maximale BLS-Intensität bei rund 2600 cm−1 detektiert, was einer Spinwellen-Wellenlänge von ungefähr 25 µm entspricht. Das maximale BLS-Signal bei der Untersuchung von Position 2 liegt bei ungefähr 150 cm−1 , was einer Wellenlänge der Spinwellen von
420 µm entspricht. In beiden Fällen wurden die Messkurven durch einen Gauss-Fit angepasst und
die Halbwertsbreite beträgt jeweils rund 1200 cm−1 .
Mit Hilfe der Wellenvektorabhängigen Messung verschiedener Antennen, kann man klar sagen,
welcher Wellenvektor am effizientesten von einer bestimmten Antenne angeregt wird. Die so gewonnenen Informationen über die wellenvektorabhänige Anregungscharakteristik der Antennen
lassen sich nun auf reine Mikrowellenexperimente übertragen, die keine Wellenvektorauflösung
bieten.
43
4.2 Parametrische Verstärkung
4.2. Parametrische Verstärkung
Im Folgenden werden die Resultate, die beim parallelen Pumpen gewonnen wurden, vorgestellt.
Bei diesem Pumpprozess werden, wie in Kapitel 2.4.2 beschrieben, Spinwellen direkt, ohne Antreiben der uniformen Mode, angeregt werden. Zur Anregung wurde ein koplanarer Wellenleiter
(Coplanar Wave Guide, CPW) von 50 µm Dicke verwendet, auf dem, wie im Fall der direkten Anregung, ein 7 µm dicker YIG-Streifen fixiert wurde. In Kapitel 3.3.2 ist der Mikrowellenaufbau,
der für die parametrische Verstärkung verwendet wurde, näher erläutert.
Die Hauptmotivation, einen Aufbau, wie den hier präsentierten, zu realisieren, war die Detektion und Analyse von Magnonen mit höherem Wellenvektor in Backward-Volumen-Geometrie. In
den vergangenen Jahren erhielt die Untersuchung von Bose-Einstein-Kondensaten von Magnonen mehr und mehr Aufmerksamkeit [13]. Wie nachfolgend in Kapitel 4.2.1 dargestellt, bietet der
verwendete Aufbau eine hervorragende Möglichkeit das Bose-Einstein-Kondensat von Magnonen
wellenvektorabhängig zu untersuchen. Außerdem ist es hiermit möglich, die für die Formation des
Bose-Einstein-Kondensates wichtige dominante Gruppe zu erforschen. Wie bereits erwähnt, ist die
dominante Gruppe diejenige mit der geringsten Dämpfung.
4.2.1 Untersuchung des Minimums des Spinwellenspektrums
Zunächst sollen die Ergebnisse vorgestellt werden, die bei der Untersuchung des Minimums des
Spinwellenspektrums erzielt wurden. Durch einen parametrischen Pumpprozess, wie er in Kapitel
2.4.2 beschrieben wurde, erzeugt ein Mikrowellenphoton zwei Magnonen mit entgegengesetztem
Wellenvektor. Diese injizierten Magnonen gehen dann in die Gruppe mit der geringsten Dämpfung bei der halben Pumpfrequenz über und relaxieren anschließend aufgrund eines 4-MagnonenKonversions-Prozesses thermisch zum Minimum des Spektrums. Hier bildet sich bei genügend
großer Mikrowellenleistung ein Bose-Einstein-Kondensat von Magnonen [13].
Verteilung im reziproken Raum
Als Bose-Einstein-Kondensat (BEC) bezeichnet man einen kollektiven quantenmechanischen Zustand identischer Teilchen mit ganzzahligem Spin (Bosonen), wenn die Teilchendichte einen kritischen Wert übersteigt. Um ein Bose-Einstein-Kondensat zu erzeugen, kann man entweder die Temperatur erniedrigen oder die Teilchendichte erhöhen. Bereits 1968 wurde vorausgesagt, dass ein
Quasi-Gleichgewichtszustand eines bosonischen Systems selbst bei relativ hohen Temperaturen
in ein Bose-Einstein-Kondensat übergehen kann [66, 67]. Voraussetzung hierfür ist das Erreichen
einer kritischen Pumprate. Magnonen haben ganzzahligen Spin und können somit in einem thermischen Gleichgewicht mit Hilfe der Bose-Einstein-Statistik beschrieben werden. Im Jahr 2006
44
4.2 Parametrische Verstärkung
(a)
(b)
Abbildung 4.4: (a) Wellenvektoraufgelöste Untersuchung des Signals vom Minimum des Spinwellenspektrums. Bei einem Wellenvektor von 49500 ± 1700 cm−1 bildet sich ein Bose-Einstein-Kondensat
von Magnonen. Die Frequenz, bei der das Spektrum aufgenommen wurde, betrug 5,6 GHz. Die
Pumpfrequenz betrug 14,05 GHz bei einem angelegten Magnetfeld von 1960 Oe. (b) Berechnete Dispersionsrelation für den Fall einer in Magnetisierungsrichtung propagierenden Spinwelle (kkH0 ).
Das berechnete Minimum liegt bei 47600 cm−1 und einer Frequenz von 5,65 GHz.
konnten Demokritov et al. [13] mithilfe der Mikrowellentechnik ein Bose-Einstein-Kondensat in
einem Magnonengas bei Raumtemperatur erzeugen. In der vorliegenden Arbeit wurde dieses wellenvektorabhängig untersucht.
Aufgrund der relativ schwachen Wechselwirkung zwischen den Magnonen bei Temperaturen weit
unterhalb der Curietemperatur TC , eignen sich Magnonengase besonders gut für die Bildung eines BECs. YIG stellt einen guten Kandidaten zur Untersuchung eines BECs dar. Zum einen besitzt es, wie in Kapitel 3.1 beschrieben, eine sehr lange Spin-Gitter-Relaxationszeit von über 1 µs.
Im Vergleich dazu liegt die Relaxationszeit der 2- bzw. 4-Magnonen-Streuung bei weniger als
200 ns. Zum anderen beträgt die durch den parametrischen Pumpprozess injezierte Magnonendichte 1018 − 1019 cm−1 [42]. Die Dichte der thermischen Magnonen bei Raumtemperatur ist zwar
mit 1021 − 1022 cm−1 [13] größer, doch der Zuwachs ist ausreichend, um ein BEC herstellen zu
können. Beide Mechanismen zusammen ermöglichen, dass die Magnonenzahl konstant bleibt und
sich ein BEC bilden kann.
In Abbildung 4.4 sind die wellenvektoraufgelösten Messergebnisse des Bose-Einstein-Kondensats
sowie die dazugehörige Dispersionsrelation zu sehen. Um der Energie- und Impulserhaltung gerecht zu werden, wurde eine parametrische Pumpfrequenz von 14,05 GHz bei einem Magnetfeld
von 1960 Oe gewählt. Das Minimum des Spinwellenspektrums wurde experimentell bei einer Frequenz von 5,6 GHz bestimmt und stimmt damit gut mit dem berechneten Wert (Abbildung 4.4
(b)) von 5,65 GHz überein. Der Wellenvektor, bei dem die maximale BLS-Intensität detektiert
45
4.2 Parametrische Verstärkung
60000
50 Watt
32 Watt
50000
BLS Intensität (a. u.)
25 Watt
40000
30000
20000
10000
0
30000
40000
50000
60000
70000
80000
-1
Wellenvektor (cm )
Abbildung 4.5: Signal vom Minimum des Spinwellenspektrums bei verschiedenen Mikrowellenleistungen: mit abnehmender Leistung sinkt das Maximum des Bose-Einstein-Kondensats. Das Magnetfeld betrug 1980 Oe und die Pumpfrequenz 14,02 GHz.
wurde, entspricht in guter Näherung dem Wellenvektor, an dem das Spinwellenspektrum sein Minimum aufweist. Dies erklärt sich dadurch, dass die Magnonen vorzugsweise zum niedrigsten
Energiezustand relaxieren. Der Relaxationsprozess ist jedoch nur für die Magnonen möglich, die
bei der Streuung in diesen Zustand Energie- und Impulserhaltung erfüllen. Die Relaxation zum
Minimum des Spinwellenspektrums stellt den wahrscheinlichsten Übergangsprozess dar und es
resultiert ein maximales BLS-Signal. Die maximale Intensität des BECs von Magnonen liegt bei
49500±1700 cm−1 und zeigt damit eine gute Übereinstimmung mit dem berechneten Minimum
der Dispersionsrelation bei 47600 cm−1 . Um die Breite des BEC-Peaks im Frequenzraum bestimmen zu können, wurden die Wellenvektoren, bei denen das BLS-Signal auf die Hälfte abgefallen
ist, ermittelt (Abbildung 4.4 (a)). Anhand der Dispersionsrelation (Abbildung 4.4 (b)) wurde nun
die Frequenzbreite berechnet. Sie beträgt in der vorgestellten Messung weniger als 10 MHz und
entspricht damit der typischen Frequenzbreite eines BECs.
Des Weiteren wurde das Bose-Einstein-Kondensat wellenvektorabhängig für verschiedenen Mikrowellenleistungen untersucht, wie in Abbildung 4.5 gezeigt. Die Pumpfrequenz betrug 14,02 GHz
bei einem Magnetfeld von 1980 Oe. Es ist klar zu erkennen, dass das Maximum des BECs weniger
stark ausgeprägt ist, je niedriger die verwendete Mikrowellenleistung ist.
46
4.2 Parametrische Verstärkung
Abbildung 4.6: Magnetfeldabängigkeit des Signal vom Minimum des Spinwellenspektrums. Diese
Messung dient dazu, das Feld zu bestimmen, bei dem die BLS-Intensität minimal wird. Hier können
kinetische Instabilitäten [68] ausgeschlossen werden. Die Pumpfrequenz betrug 14,05 GHz und das
Spektrum wurde bei einer Frequenz von 5,6 GHz aufgezeichnet.
Untersuchung der Zeitabhängigkeit
Das Minimum des Spinwellenspektrums wurde nicht nur wellenvektorabhängig beobachtet, sondern gleichzeitig zeitaufgelöst gemessen. Die zeitaufgelöste Messung bietet Informationen über
die zeitliche Entwicklung des sich formierenden Bose-Einstein-Kondensates, das heißt zu welchem Zeitpunkt das BEC gepumpt wird und wann ein Gleichgewichtszustand vorliegt.
Um kinetische Instabilitäten und andere störende Effekte auszuschließen [68], wurde vor der
eigentlichen zeitaufgelösten Messung, das Signal vom Minimum des Spinwellenspektrums in
Abhängigkeit des angelegten Magnetfeldes untersucht. Diese Messung diente lediglich dazu ein
geeignetes Magnetfeld zu finden, bei dem die BLS-Intensität minimal ist. Die Pumpfrequenz betrug 14,05 GHz und das Spektrum wurde bei einer Frequenz von 5,6 GHz aufgezeichnet. Die Ergebnisse sind in Abbildung 4.6 dargestellt. Es ist klar ein Minimum des BLS-Signals im Bereich
zwischen 1750 Oe und 1850 Oe zu erkennen. Für die weiteren Messungen wurde ein Magnetfeld
von 1750 Oe und ein Verhältnis von Pulslänge zu Repetitionsrate von 5 % gewählt. Die Resultate
der zeitaufgelösten Messungen ist in Abbildung 4.8 für verschiedene Wellenvektoren abgebildet.
Dabei ist zu berücksichtigen, dass es sich bei den dargestellten Ergebnissen um die auf 100 normierten Werte handelt. Es fällt auf, dass das lokale Maximum am Anfang des Pulses zunächst
mit steigendem Wellenvektor anwächst, bei rund 50000 cm−1 seinen maximalen Wert erreicht und
47
4.2 Parametrische Verstärkung
dann wieder abfällt. Dieses Verhalten korrespondiert zur reinen, wellenvektoraufgelösten Messung
des BEC (Abbildung 4.4), bei dem das maximale Signal ebenfalls bei 50000 cm−1 detektiert wurde. Man kann also diesen Peak am Anfang des Pulses der Bildung des BECs zuordnen. An das
Maximum am Anfang des Pulses schließt sich ein Plateau an, das dem Gleichgewichtszustand
des BECs entspricht. Zwischen den beiden Bereichen befindet sich ein lokales Minimum. Ursache
dafür könnte sein, dass sich das Signal aus der Überlagerung beider Teile (dem für das BEC charakteristischen Peak am Anfang des Pulses und dem flach verlaufenden Plateau) zusammensetzt.
Für ein genaueres Verständnis sind weitere Messungen notwendig.
Anhand der zeitaufgelösten Messung kann man jedoch klar unterscheiden, wann sich das BEC im
Aufbau befindet und wann ein Gleichgewicht erreicht ist.
In Abbildung 4.7 ist die Differenz aus maximalen BLS-Signal am Anfang des Pulses und dem
daran anschließenden Plateau gegen den Wellenvektor aufgetragen. Die Differenz wurde sowohl
für den normierten, als auch für den unnormierten Fall bestimmt und erreicht in beiden Fällen ihren
maximalen Wert ebenfalls bei 50000 cm−1 . Dies bedeutet zum einen, dass durch die Normierung
keine Informationen verloren gehen. Zum Anderen kann man den Peak am Anfang des Pulses
eindeutig dem Signal des BECs zuordnen (siehe Abbildung 4.4).
Differenz
Abbildung 4.7: Differenz zwischen dem maximalen Signal am Anfang des Pulses und dem darauf
folgenden Plateau (siehe Abbildung 4.8).
48
4.2 Parametrische Verstärkung
Abbildung 4.8: Zeitaufgelöste Messung des Signals vom Minimum des Spinwellenspektrums für verschiedene Wellenvektoren. Die Pumpfrequenz betrug 14,05 GHz und das angelegte Magnetfeld lag
bei 1750 Oe. Die Profile wurden bei 5,6 GHz aufgezeichnet.
49
4.2 Parametrische Verstärkung
Pulslänge/ Repetitionsrate
12000
100
40
BLS Intensität (a. u.)
10000
s/ 5
s/ 2
200
s
s
s/ 10
s
8000
6000
4000
2000
0
-20
-15
-10
-5
0
Abschwächung der Pumpleistung (dB)
Abbildung 4.9: BLS Signal aufgetragen gegen Abschwächung der Mikrowellenleistung für verschiedene Pulslängen und Repetitionsraten. Das Verhältnis von Pulslänge zu Repetitionsrate wurde nicht
verändert, um das Erhitzen der Probe zu vermeiden. Die Pumpfrequenz betrug 13,95 GHz bei einem
Feld von 1715 Oe. Das Signal wurde bei 7 GHz detektiert.
4.2.2 Untersuchung der dominanten Gruppe bei halber Pumpfrequenz
In diesem Kapitel wird die sogenannte dominante Gruppe untersucht, die bei der halben Pumpfrequenz auftritt. Da sie sozusagen als Quelle des sich formierenden Bose-Einstein-Kondensats von
Magnonen betrachtet werden kann, ist sie von besonderem Interesse. Außerdem tritt sie erst bei
wesentlich höheren Wellenvektoren als 40000 cm−1 auf, so dass der hier verwendete Aufbau für
ihre Detektion und Analyse prädestiniert ist.
Die Pumpfrequenz betrug in den hier vorgestellten Experimenten 13,95 GHz, so dass die dominante Gruppe bei rund 7 GHz detektiert wurde.
Abhängigkeit der dominanten Gruppe von der Mikrowellenleistung und dem Mikrowellenpuls
Um die optimale Mikrowelleneinstellungen, (das heißt Leistung, Pulslänge und Wiederholungsrate) zu bestimmen, wurde das BLS-Signal der dominanten Gruppe in Abhängigkeit der Abschwächung der Mikrowellen-Eingangsleistung für verschiedene Kombinationen aus Pulslänge
und Repetitionsrate aufgezeichnet. Dabei betrug das Verhältnis der Repetitionsrate zur Pulslänge
50
4.2 Parametrische Verstärkung
(a)
(b)
(c)
Abbildung 4.10: Darstellung der zeitlichen Entwicklung des durch den Mikrowellenpuls erzeugte Spinwellensignal. Dargestellt für verschiedene Abschwächungen der Mikrowellenleistung: (a)
−22 dB, (b) −18 dB und (c) −2 dB. Die nachfolgenden Messungen wurden bei einer Abschwächung
von −18 dB durchgeführt.
in allen Fällen 20:1, was einem Arbeitszyklus von 5 % entspricht. Dieser Wert erwies sich in vorherigen Messungen als geeignet, um die Probe nicht zu überhitzen. Diese Messung wurde lediglich
durchgeführt, um die Einstellung zu bestimmen, bei der die maximale BLS Intensität erreicht ist,
und nicht um verschiedene Arbeitszyklen zu untersuchen. Die Resultate sind in Abbildung 4.9 gezeigt. Hierbei ist anzumerken, dass die größte Abschwächung des Mikrowellensignals bei −25 dB
liegt und entsprechend die kleinste Abschwächung bei 0 dB vorliegt. Eine Abschwächung von
0 dB entspricht der vollen Leistung des Mikrowellenverstärkers von 47 dBm. Es ist klar zu erkennen, dass mit kleiner werdender Abschwächung – das heißt größerer Mikrowellenleistung – das
BLS Signal bei der halben Pumpfrequenz zunächst steil ansteigt und dann in Sättigung übergeht.
Anschließend fällt das Signal bis zur vollen Mikrowellenleistung wieder auf nahezu Null ab.
Dieses Verhalten lässt sich folgendermaßen erklären: Mit zunehmender Pumpleistung steigt die
Magnonendichte in der dominanten Gruppe stark an, was in einem Anstieg des BLS Signals resultiert. Danach relaxieren genauso viele Magnonen zum Minimum des Spinwellenspektrums,
wie durch die Mikrowellenquelle nachgeliefert werden. Das BLS Signal geht in Sättigung über.
Erhöht man die Mikrowellenleistung nun noch weiter, so dominieren nichtlineare Effekte und das
BLS-Signal nimmt wieder ab. Aus diesem Grund wurden die folgenden Messungen bei einer Abschwächung der Mikrowellenleistung von −18 dB durchgeführt. Außerdem ist anhand von Abbildung 4.9 ersichtlich, dass mit abnehmender Pulslänge respektiv Repetitionsrate die BLS Intensität
kleiner wird. Für die weiteren Messungen wurde daher die Kombination aus einer Pulslänge von
10 µs und einer Wiederholrate von 200 µs gewählt. Wie bereits in Kapitel 3.3.2 erläutert, ist es
möglich, das Spinwellensignal nicht nur optisch mittels Brillouin-Lichtstreu-Spektroskopie zu detektieren, sondern auch mithilfe eines Oszilloskops. In Abbildung 4.10 ist die durch den Mikrowellenpuls erzeugte zeitliche Entwicklung des Spinwellensignal für verschiedene Abschwächungs-
51
4.2 Parametrische Verstärkung
Signal bei 1707 Oe
Gauss Fit
20000
Signal bei 1640 Oe
Gauss Fit
8000
7000
BLS Intensität (a. u.)
BLS Intensität (a. u.)
6000
15000
10000
5000
5000
4000
3000
2000
1000
0
0
20000
40000
60000
80000
100000
120000
110000
120000
-1
Wellenvektor (cm )
130000
140000
150000
160000
170000
-1
Wellenvektor (cm )
Abbildung 4.11: Wellenvektoraufgelöste Untersuchung des Signals der dominanten Gruppe bei der
halben Pumfrequenz von 7 GHz. (a) Dargestellt ist das BLS Signal für ein Magnetfeld von 1707 Oe
und in (b) für 1640 Oe.
einstellungen zu sehen, wie sie vom Oszilloskop dargestellt wird. Von links nach rechts nimmt die
Abschwächung ab und somit die Mikrowellenleistung zu. Es ist ersichtlich, dass für eine große
Abschwächung von −22 dB (a) die linke Flanke des Pulses relativ schwach ansteigt, bevor das
Signal in Sättigung übergeht. Bei einer Abschwächung des Mikrowellensignals von −18 dB (b)
ist die Flanke bereits steiler und bevor das Signal in Sättigung übergeht, ist ein lokales Maximum
zu beobachten. Bei −2 dB Abschwächung (c) steigen die Flanken des Pulses nahezu senkrecht an
und das lokale Maximum am Anfang des Pulses ist noch stärker ausgeprägt. Die gezeigten Formen des Pulses sind charakteristisch für eine starke (a), eine moderate (b) und eine geringe (c)
Abschwächung der Mikrowellenleistung.
Verteilung der dominanten Gruppe im reziproken Raum
Alle hier vorgestellten Ergebnisse wurden bei einer Mikrowellenabschwächung von −18 dB und
einer Pulslänge von 10 µs, sowie einer Repetitionsrate von 200 µs durchgeführt (siehe vorangegangener Abschnitt). In Abbildung 4.11 ist das Signal der dominanten Gruppe bei der halben
Pumpfrequenz von 7 GHz wellenvektorabhängig abgebildet. In (a) ist das BLS-Signal für den
Fall eines Magnetfeldes von 1707 Oe und in (b) für den Fall von 1640 Oe abgebildet. Aufgrund
der verschiedenen Magnetfelder liegt die maximale BLS-Intensität bei unterschiedlichen Wellenvektoren. Für 1707 Oe liegt sie bei 61080 ± 1350 cm−1 ; für 1640 Oe wurde das Maximum bei
137720 ± 820 cm−1 detektiert. Wie bereits in Kapitel 3.5.2 erwähnt, geht der Fehler bei der Bestimmung des Wellenvektors (3.11) mit cos(∆θ) ein, so dass der Fehler für einen kleineren Einfallswinkel größer ist. Dieser Sachverhalt spiegelt sich in einer scheinbar größeren Signalbreite im
52
4.2 Parametrische Verstärkung
1780
1760
-2 dB
-18 dB
1740
-22 dB
1720
Theorie
Feld (Oe)
1700
1680
1660
1640
1620
1600
1580
1560
0
25000
50000
75000
100000
125000
150000
175000
-1
Wellenvektor (cm )
Abbildung 4.12: Von außen angelegtes Magnetfeld aufgetragen gegen den Wellenvektor für verschiedene Mikrowellenleistungen. In grün ist der theoretisch berechnete Verlauf eingezeichnet. Die
Pumpfrequenz betrug 13,95 GHz. Das Spektrum wurde bei 7 GHz aufgenommen. Erläuterungen siehe Text.
Fall des größeren Magnetfeldes (kleinerer Wellenvektor und damit auch kleinerer Einfallswinkel)
wider.
Anhand der hier vorgestellten Ergebnisse wird deutlich, dass mit den bisher realisierten Aufbauten
zur Untersuchung der Wellenvektorabhängigkeit (siehe Kapitel 3.5.2) aufgrund des großen Wellenvektors die dominante Gruppe nicht untersucht werden konnte.
4.2.3 Untersuchung der Abhängigkeit des angelegten Magnetfeldes vom Wellenvektor im Fall der dominanten Gruppe
In diesem Kapitel werden die Ergebnisse präsentiert, die bei der Untersuchung der Abhängigkeit
des von außen angelegten Magnetfeldes vom Wellenvektor erzielt wurden. Doch zunächst soll
erklärt werden, wie gemessen wurde.
Für ein festes Magnetfeld wurde bei einer bestimmten Mikrowellenabschwächung das gesamte BLS-Spektrum wellenvektorabhängig aufgezeichnet. So wurden alle Magnetfelder zwischen
1579 Oe und 1630 Oe in 3 Oe-Schritten vermessen. Anschließend wurde für eine bestimmte Wellenvektoreinstellung (das heißt eine bestimmte Position des Jochs) überprüft, bei welchem Magnetfeld das BLS-Signal bei der halben Pumpfrequenz von 7 GHz maximal war. So erhält man
53
4.2 Parametrische Verstärkung
für verschiedene Mikrowellenleistungen eine Funktion H0 (k). In Abbildung 4.12 sind die Resultate dargestellt. Dabei ist für alle drei verwendeten Mikrowellenleistungen von −2 dB, −18 dB
und −22 dB prinzipiell der gleiche Verlauf zu erkennen: Mit steigendem Wellenvektor verringert
sich das Magnetfeld, das zum Erreichen des maximalen BLS-Signals notwendig ist. Diesen Verlauf zeigt auch die theoretisch berechnete Kurve (in Grün), die man aus der Herring-Kittel-Formel
(2.34) ableiten kann. Diese lautet:
q
ω = γ (H0 + λex k 2 )(H0 + λex k 2 + 4πMs sin2 θk ) .
(4.1)
Berücksichtigt man, dass θk = 90 ° für den Fall der dominanten Gruppe ist, erhält man mit Hilfe
einiger Umformungen das Magnetfeld in Abhängigkeit des Wellenvektors:
s
ω2
H0 = −λex k 2 − 2πMs ± 4π 2 Ms 2 − 2 .
γ
(4.2)
Es ist eine Differenz von ungefähr 25 Oe zwischen der theoretisch berechneten Kurve und dem
Verlauf der Messergebnisse zu erkennen. Die Ursache hierfür liegt zum einen darin, dass der theoretisch berechnete Wert von der Volumentheorie abgeleitet wurde und in Realität ein dünner Film
verwendet wurde. Zum anderen müsste der Anisotropiebeitrag des verwendeten YIG-Streifens experimentell bestimmt werden, da davon auszugehen ist, dass bei der Präparation ein anderes Anisotropiefeld vorliegt als beim Endprodukt. Berücksichtigt man diese beiden Faktoren, so zeigen
die Messergebnisse eine gute Übereinstimmung mit der Theorie.
Es soll nun noch einmal kurz auf die Theorie des parallen Pumpens (Kapitel 2.4.2) im Allgemeinen
und die Butterfly-Kurve (Abbildung 2.7) im Besonderen eingegangen werden. Das Magnetfeld, bei
dem der Wellenvektor k ≈ 0 cm−1 beträgt, wird als kritisches Feld Hkrit bezeichnet. Wie bereits
in der Theorie (Kapitel 2.4.2) erläutert, ist das parallele Pumpen ein Schwellwertprozess: Ab einer
gewissen Mikrowellenleistung, einem kritischen Mikrowellenfeld hkrit entsprechend, kommt es zu
einem exponentiellen Anstieg von Spinwellen. Wie in Abbildung 2.7 zu sehen, wird hkrit minimal,
wenn Hkrit erreicht ist.
Der theoretisch berechnete Wert von Hkrit beträgt 1765 Oe (Schnittpunkt der berechneten Kurve
in Abbildung 4.12 grün gezeichnet) mit der y-Achse. Aus den experimentellen Daten kann man
auf ein kritisches Feld Hkrit , das zwischen 1710 Oe und 1730 Oe liegt, schließen (Schnittpunkt der
experimentell ermittelten Kurve in Abbildung 4.12 mit der y-Achse).
Bei den Messergebnissen (Abbildung 4.12) fällt eine Besonderheit auf. Bei allen eingestellten
Mikrowellenleistungen, sind bei k ≈ 50000 cm−1 und k ≈ 140000 cm−1 lokale Minima im Kurvenverlauf zu beobachten. Da diese auch bei wiederholter Messung stets bei dem selben Wellenvektor auftreten, handelt es sich hierbei um eine systematische Ursache. Wie nachfolgend erläutert,
sind diese lokalen Minima Folge der Kopplung zwischen dem magnetischen und dem elastischen
54
4.2 Parametrische Verstärkung
System (z. B. Vibrationen des Kristallgitters), die sogenannte magnetoelastische Kopplung. Die
Hauptursache dafür ist die Spin-Orbit-Kopplung.
Zunächst sollen aber die wichtigsten Formeln für die Beschreibung des elastischen Verhaltens von
Kristallen angegeben werden. Geht man davon aus, dass der Verformungszustand des Kristalls im
Rahmen einer Kontinuumstheorie beschrieben werden kann, definiert man den Verschiebungsvektor u(r) als
u(r) = r − r0
(4.3)
mit den Positionen r und r0 des verschobenen und des ursprünglichen Zustandes. Unter bestimmten Voraussetzungen [69] kann man die Deformation durch einen symmetrischen Dehnungstensor
2. Stufe beschreiben
1
ǫij =
2
∂ui ∂uj
+
∂xj ∂xi
.
(4.4)
Durch Verformungen entstehen im Festkörper Kräfte bzw. Spannungen. Die Komponenten des
Spannungstensors τkl sind definiert als diese Spannungskräfte pro Flächeneinheit. Dieser ist ebenfalls symmetrisch. Das Hooksche Gesetz liefert in erster Näherung einen linearen Zusammenhang
zwischen Spannung und Verformung
τkl =
X
cklij ǫij
(4.5)
ij
mit den Komponenten cklij des elastischen Tensors (Moduls). Da sowohl τkl und ǫij symmetrisch
sind, gilt
cklij = clkji = cklji
.
(4.6)
Die Zahl der unabhängigen Komponenten des elastischen Tensors wird weiter eingeschränkt durch
die Forderung, dass die elastische Energie eine eindeutige Funktion des Dehnungszustandes sein
muss. Daraus folgt [69]
cklij = cijkl
.
(4.7)
Mit Hilfe der Indizierung nach Voigt [69] erhält man folgende Notationen: ckkkk ≡ c11 , ckkll ≡ c12
und cklkl ≡ c44 . Für ein isotropes Medium gilt
c11 − c12 = 2c44
,
(4.8)
so dass nur zwei unabhängige Komponenten übrig bleiben. In Tabelle 4.1 sind die einzelnen Komponenten des elastischen Tensors für YIG und GGG angegeben.
Die Bewegungsgleichung der Phononen lautet
ρ
∂ 2 ui
∂ 2 uk X
=
c
klij
∂t2
∂xi ∂xj
ijl
.
(4.9)
55
4.2 Parametrische Verstärkung
H0
(a)
(b)
rein magnonisch
Hkrit
H1
vergrößerter
Ausschnitt
rein
phononisch
k1
kmax
k
Abbildung 4.13: (a) Magnetoelastische Wellen in einem Magnetfeld H0 [42]. Bei (k1 /H1 ) ist eine
Hybridisierung zwischen Phononen und Magnonen zu erkennen. (b) Vergrößerter Ausschnitt von
Abbildung 4.12, in den die berechnete Phononendispersion in orange eingezeichnet wurde.
c11 (GPa)
c12 (GPa)
c44 (GPa)
ρ ( cmg 3 )
YIG
264,75
107,7
76,4
5,17
GGG
29,05
11,49
9,02
7,08
Tabelle 4.1: Elastische Konstanten und Dichte von YIG [70] bzw. GGG [71].
Mit Hilfe des von B. Hillebrands 1987 im Rahmen seiner Doktorarbeit [72] entwickelten Programms calcdis“ wurde diese Bewegungsgleichung gelöst, um die Dispersionsrelation der akus”
tischen Phononen zu bestimmen. Dabei wurden die in Tabelle 3.1 angegebenen Komponenten des
elastischen Tensors, sowie die Dichte für YIG und GGG verwendet. Die verwendete Probe besteht
aus einer ersten YIG-Schicht, dem GGG-Substrat und einer weiteren YIG-Schicht (siehe Kapitel
3.1). Da die Schichtdicke des GGG wesentlich größer als die Phononen-Wellenlänge ist, hat der
zweite YIG-Film keinen Einfluss. Er wurde in den Berechnungen nicht berücksichtigt. In Abbildung 4.13 (b) ist ein vergrößerter Ausschnitt von Abbildung 4.12 zu sehen, in den zusätzlich die
berechnete Phononendispersion eingezeichnet wurde. Dabei ist zu berücksichtigen, dass die Abszisse für den Fall der Messwerte das Magnetfeld (links) angibt und im Fall der Dispersion die
Frequenz (rechts). In Abbildung 4.13 ist der theoretische Verlauf dargestellt (aus [42]). Aus der
Phononendispersion ergibt sich für eine Frequenz, welche der halben Pumpfrequenz von 7 GHz
entspricht, ein Wellenvektor von rund 57600 cm−1 . Dieser Wert stimmt gut mit dem beobachteten
ersten lokalen Minimum in Abbildung 4.12 überein. Für das zweite lokale Minimum konnte mit
Hilfe der calcdis“-Software bei einer Frequenz von 7 GHz keine Phononenmode gefunden wer”
den. Es ist jedoch davon auszugehen, dass hier ebenfalls Energie in eine weitere Phononenmode
56
4.2 Parametrische Verstärkung
w
qk=90°
wp/2
qk=0°
w1
w^
w2
wH
k2 k1
k
Abbildung 4.14: Auswirkung einer Verkleinerung der Pumpfrequenz bei konstantem Magnetfeld,
wenn eine Hybridisierung zwischen akustischen Phononen und Spinwellen vorliegt (aus [42]).
Erläuterungen siehe Text.
transferiert wird. Für ein genaueres Verständnis sind weitere Messungen erforderlich.
Anhand von Abbildung 4.14 soll im Fall der parametrischen Anregung erklärt werden, in welchen Zweig der Dispersionsrelation Energie gepumpt wird, wenn eine Hybridisierung zwischen
akustischen Phononen und Spinwellen vorliegt und die Pumpfrequenz (bei festem Magnetfeld)
verkleinert wird. Die magnetoelastische Kopplung resultiert in einem Anwachsen des Schwellwerts für das parallelen Pumpens. Dies ist einleuchtend, da die parametrisch angeregten Spinwellen lineare elastische Wellen anregen und dadurch gedämpft werden. Es folgt ein Anwachsen des
Schwellwertes und macht sich vor allem an den Schnittstellen bemerkbar, an denen die Phononenund die Magnonendispersion hybridisieren. Zunächst soll erwähnt werden, dass Magnonen nur
mit transversalen Phononen wechselwirken können. Der Grund hierfür ist, dass Magnonen rein
transversalen Charakter haben. Anfangs sei ωp /2 größer als ω1 (Frequenz der Phononen, siehe
Abbildung4.14). In diesem Fall ist die Anregungsschwelle nahezu genauso groß wie ohne die
magnetostatische Kopplung und es wird Energie in den θk = 90 °-Zweig gepumpt. Wenn ωp /2
ungefähr so groß ist wie ω1 steigt der Schwellwert an und es ist nun günstiger zu dem Zweig, der
durch die Hybridisierung entstanden ist, zu wechseln. Verkleinert man die Pumpfrequenz weiter, so
kann man wieder ein rein magnetisches Verhalten (ohne elastische Wechselwirkung) beobachten.
Für den Fall ωp /2 < ωH können keine Spinwellen mehr ohne magnetoelastische Wechselwirkung
angeregt werden.
In unserem Fall wurde die Frequenz festgehalten und das Magnetfeld verändert, doch das prinzipielle Verhalten ist das gleiche. Bei dem ersten lokalen Minimum in Abbildung 4.12 handelt es sich
wahrscheinlich um den Schnittpunkt (k1 /ω1 ).
57
KAPITEL 5
Zusammenfassung
Im Rahmen dieser Diplomarbeit konnten nichtlineare Spinwellen wellenvektorabhängig untersucht
werden. Die in Kapitel 4.1 vorgestellten Ergebnisse der direkten Anregung zeigen, dass der neu
konzipierte und realisierte Aufbau dafür geeignet ist, sowohl Spinwellen die parallel zur Magnetfeldrichtung, als auch Spinwellen, die senkrecht zum externen Magnetfeld verlaufen, zu detektieren. Dabei zeigte sich der erwartete Verlauf: Eine Microstrip Antenne, wie sie zur direkten Anregung von Spinwellen verwendet wurde, sollte theoretisch bei der verwendeten Frequenz Spinwellen vor allem bei einem Wellenvektor von |k| ≈ 0 cm−1 anregen. Die Ergebnisse zeigen, dass das
maximale BLS-Signal bei |k| = 0 cm−1 erreicht wird und dann rasch abfällt. Die Halbwertsbreite
bei dieser Messung betrug etwa 1700 cm−1 , was sich durch die Heisenbergsche Unschärferelation
erklären lässt.
Außerdem konnten mit Hilfe der eigens für dieses Experiment angefertigten coplanar striplines
Spinwellen unterschiedlicher Wellenlänge angeregt werden (Kapitel 4.1.3). Dazu wurde der Laserspot auf verschiedene Stellen zwischen den beiden Leitern fokussiert. Es konnte in guter Übereinstimmung mit der Theorie gezeigt werden, dass aufgrund der unterschiedlichen Abstände der
Leiter verschiedene Spinwellengruppen angeregt werden. Die Informationen über die wellenvektorabhängige Anregungscharakteristik einer bestimmten Antenne, die mit dem vorgestellten Aufbau gewonnen wurden, lassen sich anschließend auf reine Mikrowellenexperimente übertragen,
die keine Wellenvektorauflösung bieten. Die äußeren Leiter, die in den hier präsentierten Experimenten nicht verwendet wurden, sollen bei späteren Untersuchungen eingesetzt werden. In einem
reinen Mikrowellenexperiment sollen sie als anregende Antennen verwenden werden, wohingegen
die innen liegenden Antennen zur Detektion von Spinwellen dienen sollen.
In Kapitel 4.2 wurden die Ergebnisse der parametrischen Verstärkung vorgestellt. Mittels der Mikrowellentechnik wurde ein Bose-Einstein-Kondensat von Magnonen erzeugt und wellenvektorabhängig untersucht. Die Verteilung des BECs im reziproken Raum zeigt, dass sich das Kondensat
– wie erwartet – im Minimum des Spinwellenspektrums bildet.
Die zeitaufgelöste Messung des Signals vom Minimum des Spinwellenspektrums liefert Informa-
58
tionen über die zeitliche Entwicklung des sich formierenden BECs. Es stellte sich heraus, dass
das lokale Maximum am Anfang des detektierten Spinwellenpulses dem Peak der reinen wellenvektorabhängigen Messung zuzuordnen ist und charakteristisch für ein BEC von Magnonen ist.
Das an den Peak am Anfang des Pulses anschließende Minimum konnte nicht vollständig erklärt
werden. Vermutlich handelt es sich bei dem Minimum in den aufgezeichneten Profilen um eine
Überlagerung zweier Anteile: der scharfe Peak am Anfang des Pulses und der langsam entstehende Gleichgewichtszustand des BECs, der sich durch das darauf folgenden Plateau bemerkbar
macht. Für ein genaueres Verständnis der hier ablaufenden Prozesse sind weitere Untersuchungen
notwendig und konnten aufgrund der mehrere Stunden dauernden zeitaufgelösten Messungen im
Rahmen dieser Diplomarbeit nicht mehr durchgeführt werden.
Ein weiterer Teil des Kapitels 4.2 über parametrische Verstärkung beinhaltet die Präsentation der
Resultate, die bei der Untersuchung der sogenannten dominanten Gruppe gewonnen wurden. Es
konnte dabei eine deutliche Abhängigkeit der BLS-Intensität von der verwendeten Mikrowellenleistung festgestellt werden.
Bei den Experimenten zur Verteilung der dominanten Gruppe im reziproken Raum wurde gezeigt,
dass es mit dem verwendeten Aufbau möglich ist, große Wellenvektoren bis 140000 cm−1 zu detektieren. Außerdem konnte die Abhängigkeit des angelegten Magnetfeldes vom Wellenvektor im
Fall der dominante Gruppe in sehr guter Übereinstimmung mit der Theorie untersucht werden.
Dabei fiel auf, dass bei sämtlichen verwendeten Mikrowellenleistungen bei zwei verschiedenen
Wellenvektoren lokale Minima im Kurvenverlauf auftreten. Diese sind wie in Kapitel 4.2.3 gezeigt
auf die Kopplung zwischen magnetischem und elastischem System, die sogenannte magnetoelastische Kopplung, zurückzuführen. Mit Hilfe der von B. Hillebrands entwickelten Software wurde
die Dispersionsrelation von akustischen Phononen berechnet. Es zeigte sich, dass eine der Phononenmoden bei der relevanten Frequenz im Bereich des ersten Minimums existiert. Für das zweite
Minimum, welches bei größeren Wellenvektoren auftritt, konnte keine Phononenmode gefunden
werden.
Eine vollständige Automatisierung mitsamt einer Autofokus-Routine für die Messapparatur befindet sich zur Zeit im Aufbau und wird eine wesentliche Vereinfachung der Messung darstellen.
Zukünftige zeitaufgelöste Messungen des Bose-Einstein-Kondensats von Magnonen in Kombination mit der Wellenvektorauflösung sowie die genauere Untersuchung der Hybridisierung von phononischer und magnonischer Dispersion stellen eine überaus interessante Aufgabe dar und bieten
die Möglichkeit, ein genaueres Verständnis der zugrundeliegenden Prozesse zu gewinnen.
59
Literaturverzeichnis
[1] M. Baibich, J. Broto, A. Fert, F. van Dau, F. Petroff, P. Eitenne, G. Creuzet, A. Friederich,
J. Chazelas, Giant Magnetoresistance of (001)Fe/(001)Cr Magnetic Superlattices, Physical
Review Letters 61, 2472 (1988).
[2] G. Binasch, P. Grünberg, F. Saurenbach, W. Zinn, Enhanced magnetoresistance in layered
magnetic structures with antiferromagnetic interlayer exchange, Physical Review B 39, 4828
(1989).
[3] S. M. Thompson, The discovery, development and future of GMR: The Nobel Prize 2007,
Journal of Physics D: Applied Physics 41 (2008).
[4] S. S. P. Parkin, K. P. Roche, M. G. Samant, P. M. Rice, R. B. Beyers, R. E. Scheuerlein, E. J.
O’Sullivan, S. L. Brown, J. Bucchigano, D. W. Abraham, Y. Lu, M. Rooks, P. L. Troulloud,
R. A. Wanner, W. J. Gallagher, Exchange-biased magnetic tunnel junctions and application
to nonvolatile magnetic random access memory, J. Appl. Phys. 85, 5828 (1999).
[5] J. M. Slaughter, R. W. Dave, M. DeHerrera, M. Durlam, B. N. Engel, J. Janesky, N. D. Rizzo,
S. Tehrani, Fundamentals of MRAM Technology, Journal of Superconductivity: Incorporating
Novel Magnetism 15 (2002).
[6] J. R. Eshbach, Spin-Wave Propagation and the Magnetoelastic Interaction in Yttrium Iron
Garnet, Phys. Rev. Lett. 8, 357 (1962).
[7] M. Belmeguenai, F. Zighem, Y. Roussigne, S. Cherif, P. Moch, K. Westerholt, G. Woltersdorf, G. Bayreuther, Microstrip line ferromagnetic resonance and Brillouin light scattering
investigations of magnetic properties of Co2MnGe Heusler thin films, Phys. Rev. B 79 (2009).
[8] W. Ishak, Magnetostatic wave technology: A review, Proceedings of the IEEE 76, 171 (1988).
[9] M. P. Kostylev, A. A. Serga, T. Schneider, B. Leven, B. Hillebrands, Spin-wave logical gates,
Appl. Phys. Lett. 87 (2005).
60
LITERATURVERZEICHNIS
[10] K. Lee, S. Kim, Conceptual design of spin wave logic gates based on a Mach-Zehndertype spin wave interferometer for universal logic functions, Journal of Applied Physics 104
(2008).
[11] S. V. Vasiliev, V. Kruglyak, M. L. Sokolovskii, Spin wave interferometer employing a local
nonuniformity of the effective magnetic field, Journal of Applied Physics 101 (2007).
[12] A. Khitun, R. Ostroumov, K. Wang, Spin-wave utilization in a quantum computer, Physical
Review A 64 (2001).
[13] S. Demokritov, V. Demidov, O. Dzyapko, Bose-Einstein condensation of quasi-equilibrium
magnons at room temperature under pumping, Nature 443, 430 (2006).
[14] O. Büttner, M. Bauer, A. Rueff, S. O. Demokritov, B. Hillebrands, A. N. Slavin, M. P. Kostylev, B. A. Kalinikos, Space- and time-resolved Brillouin light scattering from nonlinear spinwave packets, Ultrasonics 38, 443 (2000).
[15] A. Serga, T. Schneider, B. Hillebrands, Phase-sensitive Brillouin light scattering spectroscopy from spin-wave packets, Appl. Phys. Lett. 89 (2006).
[16] A. S. Arrott, Ultrathin Magnetic Structures I, Springer, Berlin, Heidelberg, New York (1994).
[17] J. D. Jackson, Klassische Elektrodynamik, Walter de Gruyter, Berlin, New York (4. Auflage,
2006).
[18] L. Bergmann, C. Schaefer, Lehrbuch der Experimentalphysik, Bd.6, Festkörper, Gruyter
(1992).
[19] M. Hurben, C. Patton, Theory of magnetostatic waves for in-plane magnetized anisotropic
films, JMMM 163, 39 (1995).
[20] D. Stancil, Theory of Magnetostatic Waves, Springer, New York, Berlin (1993).
[21] A. Aharoni, Introduction to the Theory of Ferromagnetism, Clarendon Press, Oxford (1998).
[22] L. D. Landau, E. M. Lifshitz, On the Theory of the Dispersion of Magnetic Permeability in
Ferromagnetic Bodies, Physikalische Zeitschrift der Sowjetunion 8, 153 (1935).
[23] B. Hillebrands, Light Scattering in Solids VII, Springer-Verlag (2000).
[24] J. Miltat, G. Albuquerque, A. Thiaville, Spin Dynamics in Confined Magnetic Structures I,
Springer (2002).
[25] S. Chikazumi, Physics of Magnetism, John Wiley & Sons, New York (1959).
61
LITERATURVERZEICHNIS
[26] C. C. Tannoudji, B. Diu, F. Laloë, Quantum Mechanics, John Wiley & Sons, New York
(1977).
[27] R. Kikuchi, On the Minimum of Magnetization Reversal Time, Journal of Applied Physics 27
27, 1352 (1956).
[28] J. C. Mallinson, On Damped Gyromagnetic Precession, IEEE Transactions on Magnetism
23, 2003 (1987).
[29] T. L. Gilbert, A Phenomenological Theory of Damping in Ferromagnetic Materials, IEEE
Transactions on Magnetism 40, 3443 (2004).
[30] C. Kittel, On the Theory of Ferromagnetic Resonance Absorption, Phys. Rev. 73, 155 (1948).
[31] C. Herring, C. Kittel, On the Theory of Spin Waves in Ferromagnetic Media, Phys. Rev. 81,
869 (1951).
[32] B. A. Kalinikos, A. N. Slavin, Theory of dipole-exchange spin wave spectrum for ferromagnetic films with mixed exchange boundary conditions, Journal of Physics C 19, 7013 (1986).
[33] T. Neumann, persönliche Mitteilung .
[34] M. Hurben, C. Patton, Theory of magnetostatic waves for in-plane magnetized isotropic films,
Journal of Magnetism and Magnetic Materials 163, 263 (1995).
[35] T. Schneider, Bestimmung und Beeinflussung der Phaseneigenschaften von Spinwellen in
Yttrium-Eisen-Granat- Wellenleiterstrukturen, Diplomarbeit, TU Kaiserslautern (2005).
[36] R. W. Damon, J. R. Eshbach, Magnetostatic modes of a ferromagnet slab, Journal of Physics
and Chemistry of Solids 19, 308 (1961).
[37] H. Suhl, The Nonlinear Behavior of Ferrites at High Microwave Signal Levels, Proceedings
of the IRE 1270–1284 (1956).
[38] H. Suhl, The Theory of Magnetic Resonance at High Signal Powers, J. Phys. Chem. Solids 1,
209 (1957).
[39] R. Damon, Magnetism: A Treatise on Modern Theory and Materials Vol. 1, Academic Press,
New York (1963).
[40] M. H. Sirvetz, E. Schlömann, J. H. Saunders, L-Band Ferromagnetic Resonance Experiments
at High Peak Power Levels, Microwave Theory and Techniques, IRE Transactions on 8, 96
(1960).
62
LITERATURVERZEICHNIS
[41] U. E. E. Hoeppe, Relaxation und Spinwelleninstabilitäten in polykristallinen Ferromagneten,
Dissertation, TU Darmstadt (2003).
[42] A. G. Gurevich, G. A. Melkov, Magnetization Oscillations and Waves, CRC Press (1996).
[43] V. E., V. S. L’vov, S. S. Starobinets, Spin-wave turbulence beyond the parametric excitation
threshold, Sov. Phys. Usp. 17, 896 (1975).
[44] V. L’vov, Wave turbulence under parametric excitations, Springer-Verlag (1992).
[45] A. Kreisel, persönliche Mitteilung .
[46] E. Riedel, Moderne Anorganische Chemie, de Gruyter, Berlin, New York (2. Auflage, 2003).
[47] S. Geller, M. A. Gilleo, The Crystal Structure and Ferrimagnetism of Yttrium-Iron Garnet, J.
Phys. Chem. Solids 3, 30 (1957).
[48] N. W. Ashcroft, D. N. Mermin, Festkörperphysik:, Oldenburg Wissenschaftsverlag (2001).
[49] V. Cherepanov, I. Kolokolov, L. Victor, The saga of YIG: spectra, thermodynamics, interaction and relaxation of magnons in a complex magnet, Physics Reports (Review Section of
Physics Letters) 229, 81 (1993).
[50] MicroChemicals Datenblätter, www.microchemicals.de .
[51] Nano+Bio Center Kaiserslautern, www.nbc.uni-kl.de/ .
[52] R. N. Simons, Coplanar Waveguide Circuits, Components and Systems, Wiley Series in Microwave and Optical Engineering (2001).
[53] S. Y. Liao, Microwave Circiut Analysis and Amplifier Design, Prentic-Hall (1987).
[54] E. Hecht, Optik, Oldenburg Verlag, München, Wien (4. Auflage, 2005).
[55] W. Demtröder, Experimentalphysik 2, Springer (2. Auflage, 1999).
[56] JRS Scientific Instruments, Tandem-Fabry-Perot Interferometer TFP-1, Operators Manual,
www.jrs-si.ch (2001).
[57] R. Mock, B. Hillebrands, J. R. Sandercock, Construction and performance of a Brillouin
scattering set-up using a triple-pass tandem interferometer, Journal of Physics E. Scientific
Instruments 20, 656 (1987).
[58] J. R. Sandercock, Light scattering from surface acoustic phonons in metals and semiconductors, Solid State Communications 26, 547 (1978).
63
LITERATURVERZEICHNIS
[59] J. Sandercock, Light Scattering in Solids III, Topics in Applied Physics Vol.51, Springer,
Berlin (1982).
[60] FAST Com-Tec P7887 Datenblatt, http://www.fastcomtec.com .
[61] B. Obry, Untersuchung der Modenkopplung in magnetischen Ringen anhand zeitaufgelöster
Brillouin-Lichtstreumikroskopie, Diplomarbeit, TU Kaiserslautern (2009).
[62] W. Wettling, W. Wilber, P. Kabos, C. Patton, Light scattering from parallel-pump instabilities
in yttrium iron garnet, Phys. Rev. Lett. 51, 1680 (1983).
[63] G. Srinivasan, J. Booth, C. Patton, Characterization of magnetostatic wave devices by Brillouin light scattering, IEEE transactions on magnetics 23, 3718 (1987).
[64] P. Kabos, M. Mendik, G. Wiese, C. Patton, Spin-wave instability magnon distribution for
parallel pumping in yttrium iron garnet films at 9.5 GHz, Phys. Rev. B 55, 457 (1997).
[65] S. O. Demokritov, B. Hillebrands, A. N. Slavin, Brillouin Light Scattering Studies of Confined
Spin-waves: Linear and Nonlinear Confinement, Physics Reports 348, 441 (2001).
[66] H. Fröhlich, Bose condensation of strongly excited longitudinal electric modes, Physics Letters A 26A, 402 (1968).
[67] M. V. Mesquita, A. R. Vasconcellos, R. Luzzi, Positive-feedback-enhanced Fröhlichs BoseEinstein-like condensation in biosystems, International Journal of Quantum Chemistry 66,
177 (1998).
[68] G. A. Melkov, S. V. Sholom, Kinetic instability of spin waves in thin ferrite films, Sov. Phys.
JETP 72, 341 (1991).
[69] H. Ibach, H. Lüth, Festkörperphysik: Einführung in die Grundlagen, Springer, Berlin (2008).
[70] A. E. Clark, R. E. Stranka, Elastic Constants in Single-Crystal YIG, J. Appl. Phys. 32, 1172
(1961).
[71] L. J. Graham, R. Chang, Elastic Moduli of Single-Crystal Gadolinium Gallium Garnet, Journal of Applied Physics 41, 2247 (1970).
[72] B. Hillebrands, Lichtstreuung an akustischen Phononen und Spindwellen in Schichten und
periodischen Vielfachschichtsystemen, Dissertation, Universität Köln (1986).
64
Danksagung
Zum Schluss möchte ich mich bei allen bedanken, die durch ihre Mitarbeit und Hilfe zum Gelingen
dieser Arbeit beigetragen haben.
Prof. Dr. B. Hillebrands für die Aufnahme in die Arbeitsgruppe, die interessante Aufgabenstellung
und das in mich gesetzte Vertrauen.
Prof. Dr. M. Aeschlimann für die freundliche Übernahme des Zweitgutachtens.
Mein besonderer Dank gilt Christian Sandweg für seine Betreuung während dieses Jahres, für die
aufgebrachte Geduld und ständige Hilfsbereitschaft.
Bei Dr. Vitaliy Vasyuchka und Dr. habil. Oleksandr Serha möchte ich mich für die ausführliche
Einführung in die Thematik und die gute Zusammenarbeit bedanken.
Helmut Schultheiß, Katrin Vogt, Björn Obry und Sebastian Schäfer danke ich für die Unterstützung,
wenn Probleme bei der BLS-Spektroskopie auftraten.
Dr. Thomas Schneider und Timo Neumann danke ich für das Korrekturlesen und die wertvollen
Ratschläge.
Bei Peter Clausen, Philipp Pirro, Sebastian Hermsdörfer, Dieter Weller und Sibylle Müller sowie
allen nicht namentlich genannten Mitglieder dieser Arbeitsgruppe für ihre Hilfsbereitschaft und
die angenehme Zusammenarbeit.
Eva Rixecker, Kerstin Matura und Margot Jungfleisch danke ich für das unermüdliche Korrekturlesen.
Besonders möchte ich mich bei Thomas Sebastian bedanken, der mir während des Studiums ein
teurer und sehr geschätzter Freund geworden ist.
Meinen Eltern möchte ich einfach für alles danken. Sie haben mir das Studium überhaupt erst
ermöglicht und waren in allen Situation immer für mich da.
65
Ich versichere, dass ich die Arbeit selbstständig verfasst und keine anderen als die
angegebenen Hilfsmittel verwendet habe.
Unterschrift