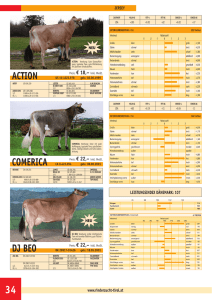
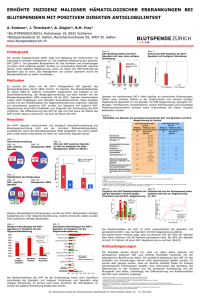
LISREL-Analyse mehrerer Gruppen

Nagl, Modelle mit latenten Variablen, Spezielle Modelle
Seite 1
LISREL-Analyse mehrerer Gruppen
Für G Gruppen können einzeln LISREL-Modelle geschätzt werden; speziell für die g. Gruppe:
Λ (xg) , Λ (yg ) , B (g ) , Γ (g ) , Φ(g) , Ψ (g) , Θ (g) , Θ (g ) . Jede Matrix kann fixierte, freie oder restringierte Parameter
enthalten.
Die nahe liegenden Fragestellungen sind zudem, inwiefern verschiedene Parameter aus unterschiedlichen
Gruppen gleich sind; speziell ob bestimmte Typen von Matrizen gleich sind:
Λ (x1)  Λ (x2)  ...  Λ (xG) oder Λ (y1)  Λ (y2)  ...  Λ (yG ) oder Θ (1)  Θ (2)  ...  Θ (G) oder
Θ (1)  Θ (2)  ...  Θ (G ) oder B (1)  B ( 2)  ...  B (G ) oder Γ (1)  Γ ( 2)  ...  Γ (G) oder
Φ (1)  Φ ( 2)  ...  Φ (G ) oder Ψ (1)  Ψ ( 2)  ...  Ψ (G ) .
Es sind aber auch möglich, durch Kombination bestimmter Matrizenfestlegungen die Gleichheit der Kovarianzmatrizen ( Σ / 1)  Σ / 2)  ...  Σ / G ) ) in den verschiedenen Gruppen zu testen: Λ (xg)  I und
Φ (1)  Φ ( 2)  ...  Φ (G ) .
Die Anzahl der verschiedenen linear unabhängigen Parameter kann wieder im wesentlichen durch Abzählen
(über alle Gruppen hinweg) bestimmt werden: t .
Die Anzahl der Freiheitsgrade:
df = G 12 (p  q)(p  q  1)  t .
G
Als Fitkriterium wird das gewichtete Fitkriterium jeder einzelnen Gruppe verwendet: F 

g 1
Ng
N
Fg . Der
natürliche Logarithmus des Likelihoodkriteriums ist:
G N
G
g
ln( L)  
(( p  q) ln( 2)  ln( Det (C g ))  Spur(S g C g1 )) =
ln( L g )
2
g 1
g 1


Beispiele: Daten (STEP Reading/Writing-Grade5/Grade7) von männlichen Kindern aus Akademiker- und
Nichtakademikerfamilien mit LISREL.
Datendatei (Labels und Varainz-Kovarianz-Matrix): EX91.DAT
READ-GR5 WRIT-GR5 READ-GR7 WRIT-GR7
281.349
184.219 182.821
216.739 171.699 283.289
198.376 153.201 208.837 246.069
READ-GR5 WRIT-GR5 READ-GR7 WRIT-GR7
174.485
134.468 161.869
129.840 118.836 228.449
102.194 97.767 136.058 180.460
A: Testen der Gleichheit der Kovarianz-Matrix
Befehlsdatei:
TESTING EQUALITY OF Covariance-Matrizen. HYPOTHESIS A. GROUP: BOYS ACADEMIC
DA NG=2 NI=4 NO=373
LA FI=EX91.DAT ;CM FI=EX91.DAT
MO NX=4 NK=4 LX=ID TD=ZE
OU EPS=1.D-10
TESTING EQUALITY OF Covariance-Matrizen. HYPOTHESIS A. GROUP: BOYS NON-ACADEMIC
DA NO=249
LA FI=EX91.DAT;CM FI=EX91.DAT
MO PH=IN
PD
OU
Nagl, Modelle mit latenten Variablen, Spezielle Modelle
Seite 2
LISREL-Regeln für die Befehlsdatei (LISREL 7 USERs GUIDE, S. 257):
 NG (=Anzahl der Gruppen) muß in der DA-Zeile der 1. Gruppe stehen.
 Falls eine Gruppe g die gleichen Optionen wie die vorige hat, kann sie entfallen,
 Mustermatrizen und Nicht-0 fixierte Werte wie auch Startwerte werden wie üblich definiert. Ein
Matrixelement (z.B. BE(4,3) mit einem oder 2 Indizes bezieht sich auf die aktuelle Gruppe. Falls eine
andere Gruppe angesprochen werden soll, muß ein weiterer Index für die Gruppe eingefügt werden (an
erster Stelle; z.B. BE(2,4,3) ist das entsprechende Element aus der 2. Gruppe).
 Für das Definieren der Gleichheitsrestriktionen zwischen den Gruppen: In der ersten Gruppe die
Elemente als frei deklarieren und in jeder nachfolgenden Gleichheit definiueren. (z.B. Soll BE(4,3) in
allen Gruppen gleich sein, dann ist angesagt: bei Gruppe 1: FR BE(4,3), bei Gruppe 2: EQ BE(1,4,3) BE(4,3) und
bei Gruppe 3: EQ BE(1,4,3) BE(4,3) usw)


Wenn eine Matrix als ID oder ZE in der 1. Gruppe spezifiziert ist, darf sie nicht als DI, FU oder SY in
einer nachfolgenden Gruppe spezifiziert werden.
Zusätzlich zur üblichen Matrixspezifikation in der MO-Zeile, sind in den MO-Zeilen der Gruppen 2 bis
G folgende Optionen möglich:
o SP Matrix hat das gleiche Muster von fixed bzw. freien Elementen
o SS (same Starting values)
o PS (same Pattern and starting values)
o IN invariant über Gruppen hinweg (d.h. gleiches fixed-free-Muster und alle in der 1. Gruppe
als frei deklarierten Elemente sind gleich in allen Gruppen).
Beispiel: Modell: x  Λ (xg)    .
TESTING EQUALITY OF FACTOR STRUCTURES. Ohne Gleichheitsforderung
DA NG=2 NI=4 NO=373
LA FI=EX91.DAT ; CM FI=EX91.DAT
MO NX=4 NK=2
FR LX 2 1 LX 4 2
VA 1 LX 1 1 LX 3 2
OU
TESTING EQUALITY OF FACTOR STRUCTURES.
DA NO=249
LA FI=EX91.DAT;CM FI=EX91.DAT
MO LX=PS
PD
OU
Chi**2=1.52, df=2, p-Wert = 0.46817
C: Restriktion: Gleichheit der Faktorenstruktur
Λ (x1)  Λ (x2)
TESTING EQUALITY OF FACTOR STRUCTURES.
DA NG=2 NI=4 NO=373
LA FI=EX91.DAT ; CM FI=EX91.DAT
MO NX=4 NK=2
FR LX 2 1 LX 4 2
VA 1 LX 1 1 LX 3 2
OU
TESTING EQUALITY OF FACTOR STRUCTURES.
DA NO=249
LA FI=EX91.DAT;CM FI=EX91.DAT
MO LX=IN
PD
OU
Nagl, Modelle mit latenten Variablen, Spezielle Modelle
Seite 3
D: Restriktion: Gleichheit der Faktorenstruktur
Λ (x1)  Λ (x2) und Θ (1)  Θ (2)
TESTING EQUALITY OF FACTOR STRUCTURES.
DA NG=2 NI=4 NO=373
LA FI=EX91.DAT ; CM FI=EX91.DAT
MO NX=4 NK=2
FR LX 2 1 LX 4 2
VA 1 LX 1 1 LX 3 2
OU
TESTING EQUALITY OF FACTOR STRUCTURES.
DA NO=249
LA FI=EX91.DAT;CM FI=EX91.DAT
MO LX=IN TD=IN
PD
OU
E: Restriktion: Gleichheit der Faktorenstruktur
Λ (x1)  Λ (x2) und Θ (1)  Θ (2) und Φ (1)  Φ (2)
TESTING EQUALITY OF FACTOR STRUCTURES.
DA NG=2 NI=4 NO=373
LA FI=EX91.DAT ; CM FI=EX91.DAT
MO NX=4 NK=2
FR LX 2 1 LX 4 2
VA 1 LX 1 1 LX 3 2
OU
TESTING EQUALITY OF FACTOR STRUCTURES.
DA NO=249
LA FI=EX91.DAT;CM FI=EX91.DAT
MO LX=IN TD=IN PH=IN
PD
OU
Übersicht über die verschiedenen Modelle
Hypothese
A
Σ / 1)  Σ / 2)
B
C
Λ (1)  Λ (2)
x
D
E
F
G
Λ (x1)

Λ (x2)
x
und Θ (1)  Θ (2)
Λ (x1)  Λ (x2) und Θ (1)  Θ (2) und Φ (1)  Φ (2)
Korrelationen der Faktoren sind gleich
Korrelationen der Faktoren sind gleich und Λ (x1)  Λ (x2)
2
38.08
1.52
5.65
df
10
2
4
p-Wert
0.0001
0.46867
0.07056
20.55
8
0.00844
35.4
11
0.00022
12.7
24.54
3
7
0.00716
0.0009
RMSEA
0.099
0.090
Nagl, Modelle mit latenten Variablen, Spezielle Modelle
Seite 4
Befehle für die Hypothesen F und G
F: TESTING EQUALITY OF FACTOR CORRELATIONS GROUP 1
DA NG=2 NI=4 NO=373
LA FI=EX91.DAT ; CM FI=EX91.DAT
MO NX=4 NK=2 PH=FI
VA 1 PH 1 1 PH 2 2
FR LX 1 1 LX 2 1 LX 3 2 LX 4 2 PH 2 1
OU
TESTING EQUALITY OF FACTOR CORRELATIONS GROUP 2
DA NO=249
LA FI=EX91.DAT ; CM FI=EX91.DAT
MO PH=IN
FR LX 1 1 LX 2 1 LX 3 2 LX 4 2
PD
OU
G: TESTING EQUALITY OF FACTOR CORRELATIONS und Ladungen GROUP 1
DA NG=2 NI=4 NO=373
LA FI=EX91.DAT ; CM FI=EX91.DAT
MO NX=4 NK=2 PH=FI
VA 1 PH 1 1 PH 2 2
FR LX 1 1 LX 2 1 LX 3 2 LX 4 2 PH 2 1
OU
TESTING EQUALITY OF FACTOR CORRELATIONS GROUP 2
DA NO=249
LA FI=EX91.DAT ; CM FI=EX91.DAT
MO PH=IN
EQ LX 1 1 1 LX 1 1
EQ LX 1 2 1 LX 2 1
EQ LX 1 3 2 LX 3 2
EQ LX 1 4 2 LX 4 2
PD
OU
Diese Modelle sind mit PROC CALIS nicht möglich.
Erweiterung auf Mittelwertstrukturen.
Das LISREL-Modell wurde so erweitert, dass auch die Mittelwerte mit modelliert werden können:
Strukturgleichungen:
η  α  Βη  Γξ  ζ
Messmodell:
y  τ y  Λ y η  ε und
x  τ x  Λxξ  δ
Der Erwartungswert für für alle Störgrößen und Messfehler wird als 0 angenommen. Der Erwartungswert von
xi wird mit kappa abgekürzt: E(ξ )  κ .
Somit gilt für den Erwartungswert von eta
Der Erwartungswert der x- und y-Werte:
E(η)  (I  Β) 1 (α  Γκ) .
μ x  τ x  Λ x κ und μ y  τ y  Λ y (I  Β) 1 (α  Γκ )
Diese Erweiterungen sind mit PROC CALIS nur möglich, falls nicht mehr als 1 Gruppe involviert ist.
Nagl, Modelle mit latenten Variablen, Spezielle Modelle
Seite 5
Modelle für latentes Wachstum
http://www.unc.edu/~curran/example.html
Messungen zu mehreren Zeitpunkten, Entwicklung über die Zeit!
TI Linear Uncondtional LTM for Antisocial Behavior
DA NI=11 NO=221 NG=1 MA=CM
LA
anti1 anti2 anti3 anti4 read1 read2 read3 read4 gen homecog subjid
RA FI=C:\SEM\Beispiele\LatentGrowth\antiread.dat
SE
1 2 3 4/
MO NY=4 NE=2 LY=FU,FI PS=SY,FI TE=SY,FI TY=FI AL=FI
LE
int slp
FR AL(1) AL(2)
VA 1.0 LY(1,1) LY(2,1) LY(3,1) LY(4,1)
VA 1.0 LY(2,2)
VA 2.0 LY(3,2)
VA 3.0 LY(4,2)
FR PS(1,1) PS(2,2) PS(2,1)
FR TE(1,1) TE(2,2) TE(3,3) TE(4,4)
EQ TE(1,1) TE(2,2) TE(3,3) TE(4,4)
PD
OU ME=ML IT=250
in SAS
DATA antiFer(TYPE=CORR); INPUT _TYPE_$ _name_ $ anti1 anti2 anti3 anti4;
DATALINES;
N . 221 221 221 221
STD . 1.53924 1.79157 1.80114 2.08456
MEAN . 1.49321 1.83710 1.87783 2.06787
CORR ANTI1 1 . . .
CORR ANTI2 0.41991 1 . .
CORR ANTI3 0.44156 0.50514 1 .
CORR ANTI4 0.42017 0.53607 0.59665 1
;
proc calis data=antiFer ucov aug;
lineqs
anti1 = 1 f1 + 0 f2 + e1,
anti2 = 1 f1 + 1 f2 + e2,
anti3 = 1 f1 + 2 f2 + e3,
anti4 = 1 f1 + 3 f2 + e4,
f1 = intm intercept + d1,
Schätzwerte der
f2 = slpm intercept + d2;
Parameter:
std
intm = 1.5543
e1-e4 = th th th th,
slpm = 0.1765
d1-d2 = ph11 ph22;
cov
d1 d2 = ph21;run;
Zusätzlich ist auch die Modellierung der Steigung und des Abschnitts möglich:
Nagl, Modelle mit latenten Variablen, Spezielle Modelle
Seite 6
in SAS
data anti; infile "C:\SEM\Beispiele\LatentGrowth\antiread.dat";
input anti1 anti2 anti3 anti4 read1 read2 read3 read4 gen homecog id;
run;
proc calis data=anti ucov aug;
lineqs
anti1 = 1 f1 + 0 f2 + e1,
anti2 = 1 f1 + 1 f2 + e2,
anti3 = 1 f1 + 2 f2 + e3,
anti4 = 1 f1 + 3 f2 + e4,
f1 = intm intercept + gamma1 gen + gamma2 homecog + d1,
f2 = slpm intercept + gamma3 gen + gamma4 homecog + d2;
std
e1-e4 = th th th th,
d1-d2 = ph11 ph22;
cov
d1 d2 = ph21;
run;
Gleichung mit Geschätzten Parametern:
f1
=
0.5716*gen
+ -0.0626*homecog
f2
=
0.0791*gen
+ -0.0452*homecog
+
+
1.8240*Intercept +
0.5465*Intercept +
in LISREL
TI Linear Condtional LTM for Antisocial Behavior
DA NI=11 NO=221 NG=1 MA=CM
LA
anti1 anti2 anti3 anti4 read1 read2 read3 read4 gen homecog subjid
RA FI=C:\SEM\Beispiele\LatentGrowth\antiread.dat
SE
1 2 3 4 9 10/
MO NY=6 NE=4 LY=FU,FI PS=SY,FI BE=FU,FI TE=SY,FI TY=FI AL=FI
LE
int slp gen homecog
FR AL(1) AL(2) AL(3) AL(4)
VA 1.0 LY(1,1) LY(2,1) LY(3,1) LY(4,1)
VA 1.0 LY(2,2)
VA 2.0 LY(3,2)
VA 3.0 LY(4,2)
VA 1.0 LY(5,3) LY(6,4)
FR PS(1,1) PS(2,2) PS(2,1)
FR PS(3,3) PS(4,4) PS(4,3)
FR TE(1,1) TE(2,2) TE(3,3) TE(4,4)
EQ TE(1,1) TE(2,2) TE(3,3) TE(4,4)
FR BE(1,3) BE(2,3) BE(1,4) BE(2,4)
PD
OU ME=ML IT=250
Variablen Measured Attribute Format Missing
d1
d2
Nagl, Modelle mit latenten Variablen, Spezielle Modelle
Seite 7
Name
anti1: child's antisocial behavior at Time 1 (f8.2) no missing data
anti2: child's antisocial behavior at Time 2 (f8.2) missing=999
anti3: child's antisocial behavior at Time 3 (f8.2) missing=999
anti4: child's antisocial behavior at Time 4 (f8.2) missing=999
read1: child's reading recognition at Time 1 (f8.2) no missing data
read2: child's reading recognition at Time 2 (f8.2) missing=999
read3: child's reading recognition at Time 3 (f8.2) missing=999
read4: child's reading recognition at Time 4 (f8.2) missing=999
gen: child's gender: female=0, male=1(f8.2) no missing data
momage: mother's age in years at Time 1 (f8.2) no missing data
kidage: child's age in years at Time 1 (f8.2) no missing data
homecog: child's cognitive stimulation at home (f8.2) no missing data
homeemo: child's emotional support at home (f8.2) no missing data
id: unique four-digit ID for every subject (f6.0) no missing data
Bemerkungen zur Analyse ordinaler bzw. dichotomer Variablen.
Falls Variablen dichotom bzw. gar ordinal sind, sind keine Analysen möglich, die multivariate Normalverteilung
voraussetzen.
Eine Möglichkeit besteht darin, ein normalverteiltes Kontinuum (z*) zu unterstellen zu unterstellen. Die
tatsächlich gemessene Variable (z) sei aber leider nur ein unvollständiger Annäherungswert; die gemessenen
Werte können dann über ein Schwellenwertmodell angenähert werden (Schwellenwerte: 1 , 2 usw)
Untere Grenze
1 <
2 <
3 <
Kontinuum
z*
z*
z*
z*
Obere Grenze
<= 1
<= 2
<= 3
Gemessener z-Wert
1
2
3
4
Falls zwei Variablen betrachtet werden (z1 und z2), könnten beide Variablen ordinal gemessen worden sein, aber
beide einer bivariaten Normalverteilung entstammen (d. h. die entsprechenden Kontinua sind bivariat
normalverteilt). Die Varianz und der Mittelwert können dabei verständlicherweise nicht geschätzt werden (meist
werden standardverteilte Normalverteilungen unterstellt).
Bezeichnungen spezieller Korrelationskoeffizienten:
z2 dichotom (aus
Nv. Kontinuum)
z1 dichotom (aus Nv. Kontinuum)
tetrachorischer
z1 ordinal (aus Nv. Kontinuum)
polychorischer
z2 ordinal (aus
Nv. Kontinuum)
polychorischer
polychorischer
z2 intervallskalierte
Variable
biserialer
polyserialer
Zusätzlich zu diesen Variablen gibt es auch sogenannte zensurierte (engl. censored) Variablen, die unten bzw.
oben abgeschnitten sind (ohne eigenen Namen).
Viele Programme können diesen Fall meistern (am besten allerdings in MPLUS). Für PROC CALIS gibt es ein
MACRO, das die entsprechende Korrelationsmatrix herstellt. Für LISREL gibt es den ‚PRE-Prozessor’
PRELIS, der die Korrelationsmatrix herstellt, die dann mit LISREL weiter verarbeitet werden kann.
Beispiel: Schwedische Schüler wurden gefragt, für wie wichtig sie verschiedene Topics (Menschenrechte,
Chancengleichheit usw.) halten: unwichtig (=1), nicht wichtig (=2) wichtig(=3) und sehr wichtig(=4).
Für die ersten 200 können die Polychorischen Korrelationen mit Hilfe von PRELIS auf der Basis der Datei
EX71.RAW berechnet werden.
PRELIS-Befehle:
TI Linear
Condtional
LTM for
Antisocial
Behavior
DA NI=11
NO=221
NG=1
MA=CM
LA
anti1 anti2
anti3 anti4
read1 read2
read3 read4
gen homecog
subjid
RA
FI=C:\SEM\B
eispiele\Laten
tGrowth\antir
ead.dat
SE
1 2 3 4 9 10/
MO NY=6
NE=4
LY=FU,FI
PS=SY,FI
BE=FU,FI
TE=SY,FI
TY=FI
AL=FI
LE
int slp gen
homecog
FR AL(1)
AL(2) AL(3)
AL(4)
VA 1.0
LY(1,1)
LY(2,1)
LY(3,1)
LY(4,1)
VA 1.0
LY(2,2)
VA 2.0
LY(3,2)
VA 3.0
LY(4,2)
VA 1.0
LY(5,3)
LY(6,4)
FR PS(1,1)
PS(2,2)
PS(2,1)
FR PS(3,3)
PS(4,4)
PS(4,3)
FR TE(1,1)
TE(2,2)
TE(3,3)
TE(4,4)
EQ TE(1,1)
TE(2,2)
TE(3,3)
TE(4,4)
FR BE(1,3)
BE(2,3)
BE(1,4)
BE(2,4)
PD
OU ME=ML
IT=250
Nagl, Modelle mit latenten Variablen, Spezielle Modelle
Seite 8
ATTITUDES OF MORALITY AND EQUALITY
DA NI=8 MI=0
LA
HUMRGHTS EQUALCON RACEPROB EQUALVAL EUTHANAS CRIMEPUN CONSCOBJ GUILT
RA=EX71.RAW
OU MA=PM PM=EX71.PML AC=EX71.ACP
Die Polychorischen Korrelationen werden in die Datei EX71.PML geschrieben (die asymptotischen Varianzen
und Kovarianzen der Polychor. Korrelationen stehen dann in der Datei EX71.ACP) und sind:
HUMRGHTS
EQUALCON
RACEPROB
EQUALVAL
EUTHANAS
CRIMEPUN
CONSCOBJ
GUILT
HUMRGHTS
1.000
0.422
0.213
0.370
0.438
0.206
0.183
0.093
EQUALCON
1.000
0.183
0.636
0.696
0.239
0.324
0.303
RACEPROB
1.000
0.262
0.303
0.265
0.323
0.238
EQUALVAL
1.000
0.688
0.406
0.355
0.323
EUTHANAS
1.000
0.204
0.238
0.327
CRIMEPUN
1.000
0.311
0.204
CONSCOBJ
GUILT
1.000
0.209
1.000
Mit Hilfe von LISREL soll nun eine konfirmatorische Faktorenanalyse (mit 2 Faktoren) durchgeführt werden.
ATTITUDES OF MORALITY AND EQUALITY
DA NI=8 NO=200 MA=PM
LA
HUMRGHTS EQUALCON RACEPROB EQUALVAL EUTHANAS CRIMEPUN CONSCOBJ GUILT
PM FI=EX71.PML; AC FI=EX71.ACP
MO NX=8 NK=2
FR LX 1 1 LX 2 1 LX 4 1 LX 5 1 LX 3 2 LX 6 2 LX 7 2 LX 8 2
PD
OU ME=WLS
In der DA-Zeile wird spezifiziert, dass die Matrix polychorische Korrelationen sind (MA=PM).
In der OU-Zeile wird die Methode WLS (ME=WLS) verlangt (bevorzugte Methode für Korrelationen in
LISREL, da sonst einige Schätzer fragwürdig sind.