AKF

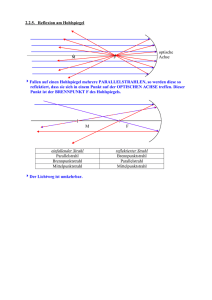
Labor Physik und Photonik
Labor zur Vorlesung Physik
Versuch 6: Autokollimationsfernrohr
1 Zur Vorbereitung
Die folgenden Begriffe sollten Sie kennen und erklären können:
Autokollimationsfernrohr, Planspiegel, Keilwinkel  , Brechungsindex, Dynameter (Messlupe),
Auflösungsgrenze, Hohlspiegel, Aperturblende, Pupillen, Krümmungsradius
2 Grundlagen: Der Autokollimator (Autokollimationsfernrohr, AKF)
2.1 Prinzip
Beim Kollimator wird durch ein Objektiv eine im Brennpunkt stehende Marke (z.B. ein Fadenkreuz)
ins Unendliche projiziert. Wenn ein Planspiegel S genau senkrecht zur optischen Achse des
Kollimators angeordnet ist, wird das Licht so reflektiert, dass das Objektiv die Marke auf sich
selbst abbildet (Autokollimation).
75926898
Seite 1 von 7
Stand: 14.05.2016
Labor Physik und Photonik
Versuch 6: Autokollimationsfernrohr
Ein AKF ist eine Kombination von Kollimator und Fernrohr, wobei das Objektiv mittels eines
halbdurchlässigen Spiegels gemeinsam genutzt wird. Zur meßbaren Beobachtung der Marke
(Fadenkreuz) wird ein Autokollimationsokular
(z.B. Gauß-Okular) verwendet, bei dem das
Fadenkreuz auf eine Skala abgebildet wird.
Wird der Spiegel S um  gegenüber der optischen Achse gekippt, dann dreht sich der reflektierte
Strahl um 2, und das Fadenkreuzbild wird auf der Skala um f K  2 verschoben, bzw. das Auge
sieht infolge der Fernrohrvergrößerung F eine Drehung um F  2 .
2.2 Mögliche Konfigurationen AKF/Prüfspiegel:
 Planspiegel
im Strahlengang: Messung von Winkeln/Winkeländerungen relativ zur
optischen Achse
 2 Planflächen einer Keilplatte im Strahlengang: Messung des Keilwinkels zwischen den
Flächen
 sphärischer Spiegel (Hohlspiegel) im Strahlengang: Messung des Spiegelradius bzw. der
Brennweite.
AKF werden in der Technik häufig verwendet, z. B. zur Messung der Geradheit von
Führungsbahnen, Planität von Führungsflächen, Bestimmung des Parallelitätsfehlers einer
planparallelen Platte, Messung von Prismenwinkeln, Krümmungsradien gekrümmter Flächen
(Linsen, Spiegel), u. a..
2.3 Das Vorsatzobjektiv (Versuchsaufbau 2) - Zur Messung des Krümmungsradius
einer Fläche
Der Abstand des Vorsatzobjektivs zum AKF ist beliebig, die Position des Prüflings (Hohlspiegels)
relativ zum Vorsatzobjektiv ist maßgebend. Das Fadenkreuz wird im AKF für 2 Positionen des
Prüflings
sichtbar.
Der
Abstand
zwischen
diesen
Positionen
entspricht
genau
dem
Krümmungsradius der zu untersuchenden Fläche.
75926898
Seite 2 von 7
Stand: 14.05.2016
Labor Physik und Photonik
Versuch 6: Autokollimationsfernrohr
2.4 Das Feinmeßokular (wie im Versuchsaufbau 3, Granitplatte als Führungsbahn,
verwendet)
Das beleuchtete Strichkreuz der Kollimator-Strichplatte wird im Okular auf einer weiteren
Strichplatte (Okularstrichplatte), die einen Winkelbereich von 30 Minuten umfaßt, abgebildet. Die
Okularstrichplatte kann mit Hilfe einer Rändelschraube in ihrer Längsrichtung verschoben werden.
Im Okular sieht man auch die Ablesemarke für eine zweite, ringförmige Strichplatte mit einer von
0-60'' (Winkelsekunden) gehenden Kreisteilung. Die Drehung dieser letzteren Strichplatte bewirkt
gleichzeitig die Kippung einer in den Strahlengang des Feinmeßokulars eingebauten
Planparallelplatte und damit eine Verschiebung des Strichkreuzbildes, wobei ein Skalenteil der
Rundskala 1 Sekunde Kippung des Meßspiegels entspricht. Das Bild des Strichkreuzes kann zu
Beginn der Messung auf einen beliebigen "runden" Ausgangswert der Minutenskala (ungefähr in
Skalenmitte) eingestellt werden. Zu diesem Zweck wird diese Skala so lange verschoben, bis das
Strichkreuzbild z.B. mit der oberen Linie der Doppelstriche zur Deckung gebracht ist. Liegt nach
einer Kippung des Meßspiegels das Bild nicht mehr genau auf dieser Linie, so wird es durch
Drehen der Kreisskala wieder mit derselben oder, falls das nicht geht, einer entsprechenden
benachbarten Linie (also wieder z.B. der oberen Linie eines Strichpaares) zur Deckung gebracht.
Der Meßwert ergibt sich dann durch Addition der Ablesewerte beider Strichplatten (lineare Skala
für die Minuten, Ringskala für die Sekunden). Das Feinmeßokular kann um 90° gedreht werden.
Dadurch ist es möglich, die Kippung des Autokollimatorspiegels sowohl um eine horizontale wie
auch um eine vertikale Achse zu messen.
2.5 Der Autokollimationsspiegel (Asp) (wie im Versuchsaufbau 3 verwendet)
ACHTUNG: Der Asp ist oberflächenbelegt und darf daher NICHT mit den Fingern berührt
werden!!
Der Autokollimationsspiegel ist auf eine Grundplatte mit drei Auflagepunkten montiert. Diese
bilden die Ecken eines gleichschenkligen Dreiecks, dessen Grundlinie parallel zur Ebene des ASP
ausgerichtet ist. Mit Hilfe einer Rändelschraube kann der ASP um eine horizontale Achse gekippt
werden. Dies ermöglicht zum einen eine Grobjustierung des ASP in Bezug auf das AFK, zum
anderen die Feststellung des Vorzeichens der Neigung bei der Bewegung des ASP längs der
Führungslinie.
75926898
Seite 3 von 7
Stand: 14.05.2016
Labor Physik und Photonik
Versuch 6: Autokollimationsfernrohr
3 Versuchsdurchführung
3.1
Bestimmung des Keilwinkels für zwei Platten (Versuchsaufbau 1)
Der Beobachter sieht zwei Bilder des Fadenkreuzes auf der Skala. Eines von der senkrecht zur
optischen Achse stehenden Vorderfläche der Platte (lichtstärker) und eines das von der
Rückfläche reflektiert wird. Diese Platte muß so justiert werden, daß die Keilrichtung mit der
Skalenrichtung übereinstimmt bzw. die Keilkante senkrecht zur Skalenteilung steht. Aus dem
Abstand e zwischen den beiden Bildern läßt sich  bestimmen. Der Brechungsindex n der Platte
ist näherungsweise mit n  1,5 anzunehmen.
Brennweite des AKF ist 500 mm, Durchmesser der Eintrittspupille (EP) 50 mm.
75926898
Seite 4 von 7
Stand: 14.05.2016
Labor Physik und Photonik
Versuch 6: Autokollimationsfernrohr
3.2 Bestimmen Sie den Krümmungsradius eines Hohlspiegels (Versuchsaufbau 2)
Zusatzobjektiv
Hohlspiegel
Autokollimatonsfernrohr
Durch das Vorsatzobjektiv wird die Marke des Kollimators M K in M K abgebildet. Stellt man
einen Hohlspiegel (Prüfling) vor das AKF, so daß seine optische Achse mit der des AKF
zusammenfällt, dann gibt es zwei Lagen 1 und 2, bei denen die Marke
MK
in der
Zwischenbildebene des Fernrohrs scharf erscheint:
1. Hohlspiegel am Ort des Markenbildes M K
2. Krümmungsmittelpunkt des Hohlspiegels fällt mit M K zusammen
Wird des Spiegel meßbar von Stellung 1 nach 2 verschoben, dann ist die Verschiebestrecke
gleich dem Krümmungsradius r .
75926898
Seite 5 von 7
Stand: 14.05.2016
Labor Physik und Photonik
Versuch 6: Autokollimationsfernrohr
3.3
Wird
Verlauf einer Führungsbahn (Versuchsaufbau 3)
vor
dem
AKF
ein
senkrecht
zu
dessen
optischer
Achse
orientierter
Spiegel
(Autokollimationsspiegel Asp) aufgestellt, so werden die aus dem Objektiv austretenden
Parallelstrahlenbündel so reflektiert, daß sie sich in der Brennebene des Fernrohrobjektivs zu
einem Bild des Strichkreuzes vereinigen. Dieses Strichkreuzbild wird mit Hilfe eines
Feinmeßokulars betrachtet. Wird der Spiegel um den Winkel  geneigt, so ändert sich die
Richtung des von ihm reflektierten Parallelstrahbündels um den Winkel 2  . Entsprechend
verschiebt sich das Bild des Strichkreuzes in der Brennebene des Objektivs. Der Winkel  (also
nicht 2  !!) kann mit Hilfe des Feinmeßokulars unmittelbar in Sekunden abgelesen werden.
Verschiebt man den Spiegel längs einer Führungslinie, so kann aus den gemessenen Kippwinkeln
des Spiegels der Oberflächenverlauf der zu untersuchenden Fläche in dieser Richtung ermittelt
werden.
3.3.1 Bestimmung des Höhenprofils einer Führungsbahn (Oberseite der Granitplatte)
Der ASp wird in Richtung der optischen Achse des AKF längs der Führungsschiene auf der zu
untersuchenden Fläche verschoben. Dabei soll die Verschiebestrecke B des ASp gleich der Höhe
des Dreiecks sein, das durch die drei Auflagepunkte gebildet wird.
Für die erste Meßstrecke (Anfangslage von ASp) wird im Feinmeßokular ein runder Wert  1
eingestellt, auf den bezogen die Meßwerte für die anderen Meßstrecken ermittelt werden.
Bezeichnet man die aufeinanderfolgenden Meßwerte mit  1 ,  2 , ....,  n wobei  1 der der ersten,
 n der der letzten Meßstrecke zugeordnete Meßwert ist, so ergeben die Differenzen
 2   1   2 ;  3   1   3 ,...  n   1   n die mittleren Neigungswinkel der betreffenden
Meßstrecken gegen die erste Meßstrecke als Bezugsstrecke. Für die entsprechenden
Höhenunterschiede zwischen Anfang und Ende der einzelnen Meßstrecken ergibt sich dann
h1  0( Bezugsstec ke)

h2  B  sin(  2 )  B    2
h3  B  sin(  3 )


hn  B  sin( n )
Der Höhenunterschied
H K des Endpunktes irgend einer Meßstrecke k bezogen auf die
Ausgangsstrecke ist dann
n
n
i 1
i 1
H K   hi  B  sin(  i )
75926898
Seite 6 von 7
Stand: 14.05.2016
Labor Physik und Photonik
Versuch 6: Autokollimationsfernrohr
4 Arbeitsprogramm
Finden Sie in der Excel-Datei Autokollimationsfernrohr.xls
75926898
Seite 7 von 7
Stand: 14.05.2016