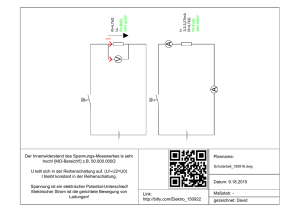
Ströme in einer Parallelschaltung
Werbung

Reihen- und Parallelschaltung Erinnere dich: Spannung, Strom, Widerstand ................................................................................................... 2 Lösungen Blatt1: Spannung, Strom, Widerstand ............................................................................................. 3 Lösungen Blatt2: Spannung, Strom, Widerstand ............................................................................................. 4 Ströme in einer Reihenschaltung.......................................................................................................................... 5 Lösungen: Ströme in einer Reihenschaltung .................................................................................................... 6 Spannungen an einer Reihenschaltung ................................................................................................................ 7 Lösungen: Spannungen an einer Reihenschaltung ........................................................................................... 8 Ersatzwiderstand der Reihenschaltung ............................................................................................................... 9 Lösungen: Ersatzwiderstand der Reihenschaltung ......................................................................................... 10 Übungen zur Reihenschaltung............................................................................................................................ 11 Lösungen: Übungen zur Reihenschaltung ...................................................................................................... 12 Ströme in einer Parallelschaltung ...................................................................................................................... 13 Lösungen: Ströme in einer Parallelschaltung ................................................................................................. 14 Spannungen an einer Parallelschaltung ............................................................................................................ 15 Lösungen: Spannungen an einer Parallelschaltung ........................................................................................ 16 Ersatzwiderstand bei einer Parallelschaltung ................................................................................................... 17 Lösungen: Ersatzwiderstand bei einer Parallelschaltung ............................................................................... 18 Übungen zur Parallelschaltung .......................................................................................................................... 19 Lösungen Blatt 1: Übungen zur Parallelschaltung ......................................................................................... 19 Lösungen Blatt 1: Übungen zur Parallelschaltung ......................................................................................... 20 Lösungen Blatt 2: Übungen zur Parallelschaltung ......................................................................................... 21 Modell zur Reihenschaltung ............................................................................................................................... 22 Modell zur Parallelschaltung .............................................................................................................................. 22 Lösung: Modell zur Reihenschaltung ............................................................................................................ 23 Lösung: Modell zur Parallelschaltung ........................................................................................................... 23 Test........................................................................................................................................................................ 24 Lösungen Blatt1: Test .................................................................................................................................... 25 Lösungen Blatt2: Test .................................................................................................................................... 26 E r i n n e r e d i c h : S p a n n u n g , S t r o m, W i d e r s t a n d 1. Erkläre den Begriff Stromstärke. Nenne Formelzeichen und Maßeinheit. 2. Erkläre den Begriff Spannung. Nenne Formelzeichen und Maßeinheit. 3. Zeichne ein "Wassermodell" für einen elektrischen Stromkreis. Ordne den Teilen des Modells denen eines elektrischen Stromkreises zu. 4. Ein Akku wird geladen. Was geschieht in ihm? 5. Was bedeuten Plus und Minus bei einer Batterie? 6. Unterscheide physikalischer und Stromrichtung. zwischen technischer 7. An einem einfachen Stromkreis soll gleichzeitig eine Strom- und Spannungsmessung durchgeführt werden. Fertige eine Schaltskizze an! 8. Durch einen Widerstand von 800 Ohm fließt ein Strom von 40 mA. Wie groß ist die anliegende Spannung? 9. An einem Widerstand von 2400 Ohm liegt eine Spannung von 18 V. Wie groß ist der fließende Strom? Beachte die Form des Lösungsweges: Gegeben - gesucht – Formel – Werte einsetzen –Ergebnis mit Maßeinheit! 10. An einem Widerstand liegt eine Spannung von 12 V, der fließende Strom beträgt 2,4 mA. Wie groß ist er? 11. Wie lautet das Ohmsche Gesetz, was sagt es aus? 12. An einem einfachen Stromkreis wurde eine Stromund Spannungsmessung durchgeführt und ein zugehöriges Meßprotokoll erstellt. Nenne und beschreibe die Möglichkeiten, um festzustellen, ob das Ohmsche Gesetz gilt. 13. Wie hat man sich den inneren Aufbau eines Drahtes vorzustellen? 14. Was geschieht und wie äußert sich das, wenn ein stromdurchflossener Leiter mit einem Bunsenbrenner erhitzt wird? 15. Welche Bedeutung hat das Wort Widerstand? 16. Erkläre, warum das Ohmsche Gesetz für eine Lampe nicht gilt. 17. Baue eine Reihenschaltung und eine Parallelschaltung aus je zwei Lampen auf. a) Fertige je Schaltung eine Skizze an. b)Was ist zu beobachten, wenn eine Lampe ausgedreht wird? c) Erklären die unterschiedlichen Beobachtungen. Lösungen Blatt1: Spannung, Strom, Widerstand 1. Stromstärke: Die Menge an Ladungen (Elektronen), die in einer bestimmten Zeit die Messstelle in einem Stromkreis passieren. Formelzeichen: I Maßeinheit: A (Ampere) 2. Spannung: Der Ladungsunterschied zwischen Pluspol und Minuspol. Formelzeichen: U Maßeinheit: V (Volt) 3. Behälter Batterie Wasserstandsunterschied Spannung Wasserrad mit Last Widerstand 4. Pluspol: Minuspol: 5. Wasser fließendes Wasser Absperrventil Rohre Elektronen Strom Schalter Leiter (Kabel) Mangel an Ladung (zu wenige Elektronen) Überschuss an Ladung (zu viele Elektronen) Ein Akku wird geladen. Was geschieht in ihm? Vom Pluspol werden Elektronen abgezogen, zum Minuspol werden Elektronen gedrückt 6. Physikalische Stromrichtung: Technischer Stromrichtung Der Strom fließt vom Minuspol zum Pluspol. Der Stromrichtung wird vom Pluspol zum Minuspol dargestellt. 7. Schaltskizze eines Stromkreises mit Strom- und Spannungsmessung: 8. Gegeben: I = 40mA, R = 800Ω Gesucht: U U = I ·R = 40mA · 800Ω = 32 000mV = 32V Lösungen Blatt2: Spannung, Strom, Widerstand 9. Gegeben: U = 18V, Gesucht: I R = 2400Ω 10. Gegeben: U = 12V, Gesucht: R I = 2,4mA I U 18 V 18000 mV 7,5mA R 2400 2400 R U 12 V 12000 mV 5000 I 2,4mA 2,4mA 11. Ohmsches Gesetz: Die Stromstärke ist der anliegenden Spannung proportional. Wird die Spannung verdoppelt (x-mal so groß), so ist auch die Stromstärke doppelt (x-mal) so groß. 12. 13. An einem einfachen Stromkreis wurde eine Strom- und Spannungsmessung durchgeführt und ein zugehöriges Messprotokoll erstellt. Nenne und beschreibe die Möglichkeiten, um festzustellen, ob das Ohmsche Gesetz gilt. Diagramm zeichnen: Zeichne ein U-I-Diagramm. Die Punkte im Diagramm liegen (fast) auf einer Geraden. Quotienten bilden: Bilde die Quotienten U/I. Alle Quotienten (Ergebnisse) sind (fast gleich groß.) Wie hat man sich den inneren Aufbau eines Drahtes vorzustellen? Ein Draht besteht aus vielen Atomen, die um ihre festen Plätze schwingen. Zwischen ihnen bewegen sich unregelmäßig die freien Elektronen in alle Richtungen, vergleichbar einem Mückenschwarm, der an einer Stelle steht. Was geschieht und wie äußert sich das, wenn ein stromdurchflossener Leiter mit einem Bunsenbrenner erhitzt wird? Der Draht glüht, die Stromstärke sinkt. Die Atome des Drahtes schwingen stärker um ihre Plätze und behindern stärker die Bewegung der Elektronen. 14. Welche Bedeutung hat das Wort Widerstand? a) Die Behinderung des fließenden Stromes. b) Der Quotient U/I heißt Widerstand. 15. Ohmsches Gesetz deutet, dass der Quotient aus Spannung und Stromstärke, also der Widerstand, konstant bleibt. Bei einer kleinen Spannung glüht der Draht nicht, die Elektronen können sich „normal“ durch den Leiter bewegen. Bei der Betriebsspannung glüht der Draht. Die Atome des Drahtes schwingen um ihre Plätze und behindern die Bewegung der Elektronen. Der Widerstand des Drahtes wächst. 16. Baue eine Reihenschaltung und eine Parallelschaltung aus je zwei Lampen auf. a) Fertige je Schaltung eine Skizze an. b)Was ist zu beobachten, wenn eine Lampe ausgedreht wird? c) Erklären die unterschiedlichen Beobachtungen. Reihenschaltung: Dreht man eine Lampe heraus, verlöschen beide. Beide Lampen haben einen gemeinsamen Stromkreis. Parallelschaltung: Dreht man eine Lampe heraus, leuchtet die andere weiter. Jede Lampe hat einen eigenen Stromkreis. S t r ö me i n e i n e r R e i h e n s c h a l t u n g 1. Skizziere eine Reihenschaltung aus zwei Widerständen unterschiedlicher Größe und der Batterie. Zeichne dort Amperemeter ein, wo Ströme gemessen werden können. Widerstand: 2. Stelle die Reihenschaltung im Wassermodell dar. Ergänze dazu die Skizze und ordne den Teilen des Modells die Teile der Reihenschaltung zu. voller Behälter leerer Behälter 3. Der elektrische Strom wird im Modell durch ....................................................... dargestellt. Wasser-Stromstärken kann man mit Wasseruhren messen. Zeichne dort Wasseruhren ein, wo möglicherweise unterschiedlich große Ströme fließen. Wasser-Ströme können in der Maßeinheit ........................... gemessen werden. 4. Stelle gegenüber und ergänze: Modell Elektrischer Stromkreis Bezeichnung Größe Wasser-Stromstärke aus dem vollen Tank in 60 l/s das erste Wasserrad. Bezeichnung Größe 600 mA Wasser-Stromstärke durch das "kleine" Wasserrad. Wasser-Stromstärke durch das "große" Wasserrad. 5. Schalte zwei Widerstände in Reihe. Miss nacheinander mit einem Amperemeter die Ströme. Kontrolliere die Batteriespannung. (Füge in deine Schaltskizze ein Voltmeter ein) a. b. ; R2 = 100 UBatt = 12V R1 = 200 I1 = .............. ; I2 = .............. ; R2 = 500 UBatt = 12V R1 = 100 I1 = .............. ; I2 = .............. ; IBatt = .............. ; IBatt = .............. 6. Sind die Messwerte andere, wenn die Reihenfolge der Widerstände vertauscht wird? Messen! 7. Vergleiche den Batteriestrom mit den Strömen durch die Widerstände. Deute die Messwerte im Wassermodell. Formuliere sprachlich und mathematisch ein Ergebnis. Lösungen: Ströme in einer Reihenschaltung 1. Skizziere eine Reihenschaltung aus zwei Widerständen unterschiedlicher Größe und der Batterie. Zeichne dort Amperemeter ein, wo Ströme gemessen werden können. Widerstand: 2. Stelle die Reihenschaltung im Wassermodell dar. Ergänze dazu die Skizze und ordne den Teilen des Modells die Teile der Reihenschaltung zu. 3. Der elektrische Strom wird im Modell durch fließendes Wasser dargestellt. Wasser-Stromstärken kann man mit Wasseruhren messen. Zeichne dort Wasseruhren ein, wo möglicherweise unterschiedlich große Ströme fließen. Wasser-Ströme können in der Maßeinheit Liter pro Sekunde gemessen werden. 4. Stelle gegenüber und ergänze: Hier sollen Vermutungen geäußert werde, die können nicht falsch sein. Modell Elektrischer Stromkreis Bezeichnung Größe Wasser-Stromstärke aus dem vollen Tank in 60 l/s das erste Wasserrad. Bezeichnung Strom zwischen Minuspol und großem Widerstand. Größe 600 mA Wasser-Stromstärke durch das "kleine" Wasserrad. 60 l/s Strom zwischen den Widerständen. 600 mA Wasser-Stromstärke durch das "große" Wasserrad. 60 l/s Strom zwischen kleinem Widerstand und Pluspol. 600 mA 5. Schalte zwei Widerstände in Reihe. Miss nacheinander mit einem Amperemeter die Ströme. Kontrolliere die Batteriespannung. (Füge in deine Schaltskizze ein Voltmeter ein) R1 = 200 ; R2 = 100 a. b. UBatt = 12V I1 = 40mA ; I2 = 40mA ; ; R2 = 500 UBatt = 12V R1 = 100 I1 = 20mA ; I2 = 20mA ; IBatt = 40mA IBatt = 20mA 6. Sind die Messwerte andere, wenn die Reihenfolge der Widerstände vertauscht wird? Messen! Die Reihenfolge der Widerstände hat keinen Einfluss. 7. Vergleiche den Batteriestrom mit den Strömen durch die Widerstände. Deute die Messwerte im Wassermodell. Formuliere sprachlich und mathematisch ein Ergebnis. Die Ströme sind stets gleich groß: IBatt = I1 = I2. Die Größe des Stromes ist aber von der Größe der Widerständen abhängig. Spannungen an einer Reihenschaltung 1. Skizziere eine Reihenschaltung mit den Widerständen (R1 = 200 ; R2 = 100 ) und einer Batterie. Zeichne dort Spannungsmesser ein, wo Spannungen gemessen werden können. Widerstand: 2. Stelle die Reihenschaltung im Wassermodell dar. .... voller Behälter leerer Behälter 3. Die elektrische Spannung der Batterie wird im Modell ......................................................................... ............................................... dargestellt. Der Wasserdruck treibt die Wasserräder an. Der Wasserdruck wird am großem und am kleinen Wasserrad gemindert. Zeichne Druckmesser ein, die den äußeren Druck und den Druck an den Wasserrädern messen. 4. Stelle gegenüber und ergänze: Modell Bezeichnung Druck zwischen dem vollen und dem leeren Behälter Elektrischer Stromkreis Größe 5 bar Bezeichnung Größe 12 V Druckunterschied durch das kleine Wasserrad Druckunterschied durch das große Wasserrad 5. Schalte die oben genannten Widerstände in Reihe und miss die Batteriespannung und die Spannungen an den Widerständen. 1. UBatt = 12V R1 = 200 U1 = .............. 2. UBatt = 9V U1 = .............. ; R2 = 100 ; U2 = .............. ; U2 = .............. 6. Sieh dir die Werte für die Batteriespannung und die Spannungen an den Widerständen an. Formuliere sprachlich und mathematisch ein Ergebnis. 7. Prüfe die Spannungen an den Widerstanden bei folgen den Kombinationen: 1. UBatt = 12V R1 = 50, R2 = 100 U1 = .............. ; U2 = .............. 2. UBatt = 12V R1 = 100, R2 = 500 U1 = .............. ; U2 = .............. Was fällt dir auf? Formuliere den Zusammenhang schriftlich. Lösungen: Spannungen an einer Reihenschaltung 1. Skizziere eine Reihenschaltung mit den Widerständen (R1 = 200 ; R2 = 100 ) und einer Batterie. Zeichne dort Spannungsmesser ein, wo Spannungen gemessen werden können. 2. Stelle die Reihenschaltung im Wassermodell dar. 3. Die elektrische Spannung der Batterie wird im Modell durch unterschiedliche Wasserstände in den Behältern dargestellt. Der Wasserdruck treibt die Wasserräder an. Der Wasserdruck wird am großem und am kleinen Wasserrad gemindert. Zeichne Druckmesser ein, die den äußeren Druck und den Druck an den Wasserrädern messen. 4. Stelle gegenüber und ergänze: Hier sollen Vermutungen geäußert werde, die können nicht falsch sein. Modell Bezeichnung Druck zwischen dem vollen und dem leeren Behälter Elektrischer Stromkreis Größe 5 bar Bezeichnung Batteriespannung Größe 12 V Druckunterschied durch das kleine Wasserrad 5 bar Spannung am großen Widerstand 12 V Druckunterschied durch das große Wasserrad 5 bar Spannung am kleinen Widerstand 12 V 5. Schalte die oben genannten Widerstände in Reihe und miss die Batteriespannung und die Spannungen an den Widerständen. 1. UBatt = 12V R1 = 200 U1 = 8V 2. UBatt = 9V U1 = 6V ; ; U2 = 4V ; U2 = 3V R2 = 100 6. Sieh dir die Werte für die Batteriespannung und die Spannungen an den Widerständen an. Formuliere sprachlich und mathematisch ein Ergebnis. Addiert man die Spannungen an den Widerständen, ergibt sich die Batteriespannung: UBatt = U1 + U2 7. Prüfe die Spannungen an den Widerstanden bei folgen den Kombinationen: 1. UBatt = 12V R1 = 50, R2 = 100 U1 = 4V ; U2 = 8V 2. UBatt = 12V R1 = 100, R2 = 500 U1 = 2V ; U2 = 10V Was fällt dir auf? Formuliere den Zusammenhang schriftlich. - Am größeren Widerstand liegt die größere Spannung. - Die Spannungen und Widerstände sind proportional: doppelt so großer Widerstand, doppelt so große Spannung. Ersatzwiderstand der Reihenschaltung 1. Stelle eine Reihenschaltung zweier Widerstände unterschiedlicher Größe im Wassermodell dar. voller Behälter leerer Behälter 2. Der elektrische Widerstand wird im Modell durch .................................................................. dargestellt. Die Wasserräder hemmen den Wasserstrom. Will man die beiden Wasserräder durch ein einziges ersetzen, muss das Ersatzrad so beschaffen sein, das es den Wasserstrom in gleicher Stärke hemmt wie zwei Räder in Reihe. Gleiche Hemmung bedeutet : .......................................................................................................................................................................... .......................................................................................................................................................................... 3. Skizziere eine Reihenschaltung aus drei Widerständen R1 = 200 , R2 = 200 und R3 = 100 mit einer Batterie. Zeichne ein Amperemeter zur Strommessung und ein Voltmeter zur Messung der Batteriespannung ein. 4. Schalte die drei Widerstände in Reihe. Miss für die Batteriespannung UBatt = 12V den Batteriestrom. UBatt = 12V IBatt = ............... geschätzt: RReihe = ........... 5. Ersetze die drei Widerstände der Schaltung durch einen einzigen. Vergleiche dessen Größe mit den Werten der Einzelwiderstände. Formuliere mathematisch und sprachlich (Aufgabe 6), wie man den Ersatzwiderstand in einer Reihenschaltung ermittelt. RReihe = ................................................ 6. Der Ersatzwiderstand ist ein wirklicher Ersatz für die Einzelwiderstände, wenn ........................................................................................................................................................................... 7. Den Ersatzwiderstand RReihe kann man berechnen, indem man die Batteriespannung durch den Batteriestrom teilt. Rechne für die Reihenschaltung R1 = 200 , R2 = 200 und R3 = 100 nach: UBatt = 12V, IBatt = ............. Lösungen: Ersatzwiderstand der Reihenschaltung 1) Stelle eine Reihenschaltung zweier Widerstände unterschiedlicher Größe im Wassermodell dar. 2) Der elektrische Widerstand wird im Modell durch Wasserräder mit anhängender Last dargestellt. Die Wasserräder hemmen den Wasserstrom. Will man die beiden Lasten durch ein einzige ersetzen, muss der Ersatz so beschaffen sein, das es den Wasserstrom in gleicher Stärke hemmt wie zwei einzelne Lasten in Reihe. Gleiche Hemmung bedeutet : Bei gleich starkem Wasserdruck muss ein gleich starker Wasserstrom fließen. 3) Skizziere eine Reihenschaltung aus drei Widerständen R1 = 200, R2 = 200 und R3 = 100 mit einer Batterie. Zeichne ein Amperemeter zur Strommessung und ein Voltmeter zur Messung der Batteriespannung ein. 4) Schalte die drei Widerstände in Reihe. Miss für die Batteriespannung UBatt = 12V den Batteriestrom. UBatt = 12V geschätzt: RReihe = 800Ω IBatt = 24 mA 5) Ersetze die drei Widerstände der Schaltung durch einen einzigen. Vergleiche dessen Größe mit den Werten der Einzelwiderstände. Formuliere sprachlich und mathematisch, wie man den Ersatzwiderstand in einer Reihenschaltung ermittelt. RReihe = R1 + R2 6) Der Ersatzwiderstand ist ein wirklicher Ersatz für die Einzelwiderstände, wenn bei gleich großer Spannung durch den Ersatzwiderstand ein gleich großer Strom fließt wie durch die Reihenschaltung. 7) Den Ersatzwiderstand RReihe kann man berechnen, indem man die Batteriespannung durch den Batteriestrom teilt. Rechne für die Reihenschaltung R1 = 200 , R2 = 200 und R3 = 100 nach: UBatt = 12V, IBatt = 24mA IRe ihe UBatt 12000 mV 500 IBatt 24mA Übungen zur Reihenschaltung 1. Reihenschaltung: UBatt = 18V, R1 = 200Ω, ges.: RReihe, I, R2 = 300Ω U1, U2 2. Durch die Reihenschaltung der Widerstände 200 und 100 fließt ein Strom von 50 mA. A) Wie groß sind die Spannungen an den Widerständen? B) Wie groß ist die Batteriespannung? 3. Reihenschaltung: UBatt = 10V, I. = 200mA ges.: RReihe, R1, U1 = 4V R 2, U2 4. Ein Signallämpchen einer Modelleisenbahn hat folgende Kenndaten: 4V, 0,1A. In der Anlage steht jedoch nur eine Spannung von 9V zur Verfügung. A) Was ist zu tun ? Fertige eine Schaltskizze an. B) Berechne die Größe des Vorwiderstandes. 5. Ein Widerstand liegt an einer Batterie von 12V, es fließt ein Strom von 100mA. A) Wie groß ist der Widerstand? Zu diesem Widerstand wird ein gleich großer in Reihe geschaltet. B) Wie groß ist der Widerstand der Reihenschaltung? C) Wie groß sind die Spannungen an den Widerständen? D) Wie groß ist der Batteriestrom? 6. Zeichne ein Messschaltung: Eine Reihenschaltung aus einer Glühlampe und einem Widerstand soll untersucht werden. Die Schaltung liegt an einer 9V Batterie. Die Spannung an der Glühlampe wird gemessen. Außerdem befindet sich ein Amperemeter in der Schaltung. 7. Die Kerzen einer Christbaumbeleuchtung benötigen eine Spannung von 22V. Die Netzspannung beträgt 220V. Zeichne das Schaltbild. 8. An die Anschlüsse der nebenstehenden Schaltung wird paarweise eine Spannung von 6 V gelegt. Es fließen folgende Ströme: Anschluss 1 und 3 : 10mA Anschluss 2 und 3 : 15mA Anschluss 1 und 2 : 20mA Lösungen: Übungen zur Reihenschaltung 1. Gegeben: Reihenschaltung: UBatt = 18V, R1 = 200Ω, R2 = 300Ω Rreihe = R1 + R2 = 200Ω + 300Ω = 500Ω IRe ihe 2. 3. UBatt 18 V 0,036 A R Re ihe 500 IReihe = I1 = I2 U1 = I1· R1 = 0,036A · 200Ω = 7,2V U2 = UBatt – U1 = 18V – 7,2V = 11,8V Gegeben: Reihenschaltung: R1 = 200Ω, I = 50mA, A) U1 = I1· R1 = 0,05A · 200Ω = 10V, B) UBatt = U1 + U2 = 15V Gegeben: Reihenschaltung: R2 = 100Ω U2 = I2· R1 = 0,05A · 100Ω = 5V UBatt = 10V, IBatt = 200mA U1 = 4V I = I1 = I2 R Re ihe UBatt 10 V 50 IBatt 0,2A R1 R2 = RReihe – R1 = 50Ω - 20Ω = 30Ω 4. U1 4V 20 I1 0,2A U2 = UBatt – U1 = 10V – 4V = 6V Man muss einen Widerstand in Reihe schalten. Gegeben: ULampe = 4V, ILampe = 0,1A UWiderstand = 9V – 4V = 5V U 5V R Widers tan d 50 ILampe 0,1A 5. A) Gegeben: U = 12V, I = 0,1A U 12 V B) RReihe = 2 · 120Ω = 240Ω R 120 I 0,1A C) gleich große Widerstände gleich große Spannungen: 6V D) IBatt UBatt 12 V 0,05 A R Re ihe 240 7. 6. 8. Durch Rechnen und dann Probieren findet man die dargestellte Lösung. U = 6V Anschluss 1 und 3 : 10mA U 6V R 600 I 0,01A Anschluss 2 und 3 : 15mA R = 400Ω Anschluss 1 und 2 : 20mA R = 300Ω S t r ö me i n e i n e r P a r a l l e l s c h a l t u n g 1. Skizziere eine Parallelschaltung aus zwei Widerständen unterschiedlicher Größe und der Batterie. Zeichne dort Amperemeter ein, wo Ströme gemessen werden können. Widerstand: 2. Stelle die Parallelschaltung zweier Widerstände im Wassermodell dar. voller Behälter leerer Behälter 3. Der elektrische Strom wird im Modell durch ........................................................ dargestellt. Wasser-Stromstärken kann man mit Wasseruhren messen. Zeichne dort Wasseruhren ein, wo möglicherweise unterschiedlich große Ströme fließen. Wasser-Ströme können in der Maßeinheit ............................ gemessen werden. 4. Stelle gegenüber und ergänze: Modell Bezeichnung Größe Wasser-Stromstärke aus dem vollen Tank. 60 l/s Elektrischer Stromkreis Bezeichnung Größe 600 mA Wasser-Stromstärke durch das Was-serrad mit dem kleineren Gewicht. Wasser-Stromstärke durch das Was-serrad mit dem kleineren Gewicht. 5. Schalte zwei Widerstände parallel. Miss nacheinander mit einem Amperemeter die Ströme. Kontrolliere die Batteriespannung. (Füge in deine Schaltskizze ein Voltmeter ein) 1. 2. UBatt = 12V UBatt = 12V R1 = 200 I1 = .............. ; R2 = 100 ; I2 = .............. R1 = 100 ; R2 = 500 I1 = .............. ; I2 = .............. ; IBatt = .............. ; IBatt = .............. 6. Vergleiche den Batteriestrom mit den Strömen durch die Widerstände. Deute die Messwerte im Wassermodell. Vergleiche die Größe der Widerstande mit der Größe der durchfließenden Ströme. Was fällt auf. Formuliere sprachlich und mathematisch ein Ergebnis. 7. Schalte einen 500 - Widerstand in Reihe mit einer Glühlampe. Stelle die Spannung so ein, dass der Glühfaden gerade glimmt. Schalte dann nacheinander zwei weitere Widerstände parallel zum 500 Widerstand. Fertige erst eine Schaltskizze an. Notiere deine Beobachtung, deute sie schriftlich. Lösungen: Ströme in einer Parallelschaltung 1) Skizziere eine Parallelschaltung aus zwei Widerständen unterschiedlicher Größe und der Batterie. Zeichne dort Amperemeter ein, wo Ströme gemessen werden können. Widerstand 2) Stelle die Parallelschaltung zweier Widerstände im Wassermodell dar. 3) Der elektrische Strom wird im Modell durch fließendes Wasser dargestellt. Wasser-Stromstärken kann man mit Wasseruhren messen. Zeichne dort Wasseruhren ein, wo möglicherweise unterschiedlich große Ströme fließen. Wasser-Ströme können in der Maßeinheit Liter je Sekunde gemessen werden. 4) Stelle gegenüber und ergänze: Hier sollen Vermutungen geäußert werde, die können nicht falsch sein. Modell Elektrischer Stromkreis Bezeichnung Größe Bezeichnung Größe Wasser-Stromstärke aus dem vollen Tank. 60 l/s Stromstärke aus der Batterie. 600 mA Wasser-Stromstärke durch das Wasserrad 20 l/s Stromstärke durch den großen 200 mA mit dem kleineren Gewicht. Widerstand. Wasser-Stromstärke durch das Wasserrad 40 l/s Stromstärke durch den kleinen 400 mA mit dem kleineren Gewicht. Widerstand. 5. 6. 7. Schalte zwei Widerstände parallel. Miss nacheinander mit einem Amperemeter die Ströme. Kontrolliere die Batteriespannung. (Füge in deine Schaltskizze ein Voltmeter ein) R1 = 200 ; R2 = 100 UBatt = 12V I1 = 60mA ; I2 = 120mA ; ; R2 = 500 UBatt = 12V R1 = 100 I1 = 120mA ; I2 = 24mA ; IBatt = 180mA IBatt = 144mA Vergleiche den Batteriestrom mit den Strömen durch die Widerstände. Deute die Messwerte im Wassermodell. Vergleiche die Größe der Widerstande mit der Größe der durchfließenden Ströme. Was fällt auf. Formuliere sprachlich und mathematisch ein Ergebnis. - Addiert man die Ströme durch die Widerstände, ergibt sich der Batteriestrom: I Batt = I1 + I2. - Durch den kleineren Widerstand fließt der größere Strom. - Die Ströme sind den Widerständen umgekehrt proportional: Doppelter Widerstand halb so großer Strom. Schalte einen 500 - Widerstand in Reihe mit einer Glühlampe. Stelle die Spannung so ein, dass der Glühfaden gerade glimmt. Schalte dann nacheinander zwei weitere Widerstände parallel zum 500 Widerstand. Fertige erst eine Schaltskizze an. Notiere deine Beobachtung, deute sie schriftlich. Beobachtung: Mit jedem Zuschalten eines Widerstandes wird die Lampe heller Deutung: Mit jedem Zuschalten eines Widerstandes wird der Batteriestrom größer, da sich die Strome durch jeden Widerstand in der Zuleitung addieren. Spannungen an einer Parallelschaltung 1. Skizziere eine Parallelschaltung mit den Widerständen (R1 = 200 ; R2 = 100 ) und einer Batterie. Zeichne dort Spannungsmesser ein, wo Spannungen gemessen werden können. 2. Stelle die Parallelschaltung zweier Widerstände im Wassermodell dar. voller Behälter leerer Behalter 3. Die elektrische Spannung der Batterie wird im Modell durch .................................................................. ................................................ dargestellt. Der Wasserdruck treibt die Wasserräder an. Der Wasserdruck wird am großem und am kleinen Wasserrad gemindert. Zeichne Druckmesser ein, die den äußeren Druck und den Druck an den Wasserrädern messen. 4. Stelle gegenüber und ergänze: Modell Bezeichnung Druck zwischen dem vollen und dem leeren Behälter Elektrischer Stromkreis Bezeichnung Größe 12 V Größe 5 bar Druckunterschied durch das Kleine Wasserrad Druckunterschied durch das Große Wasserrad 5. Schalte die oben genannten Widerstände parallel und miss die Batteriespannung und die Spannungen an den Widerständen. R1 = 200 ; R2 = 100 1. UBatt = 12V U1 = .............. ; U2 = .............. 2. UBatt = 9V U1 = .............. ; U2 = .............. 6. Sieh dir die Werte für die Batteriespannung und die Spannungen an den Widerständen an. Formuliere sprachlich und mathematisch ein Ergebnis. ......................................................................................................................................................................... 7. Prüfe die Spannungen an den Widerstanden bei folgen den Kombinationen: UBatt = 12V R1 = 100, R2 = 500 U1 = ..............; U2 =.............. Was fällt dir auf? Formuliere den Zusammenhang schriftlich. Lösungen: Spannungen an einer Parallelschaltung 1) Skizziere eine Parallelschaltung mit den Widerständen (R1 = 200 ; R2 = 100 ) und einer Batterie. Zeichne dort Spannungsmesser ein, wo Spannungen gemessen werden können. 2) Stelle die Parallelschaltung zweier Widerstände im Wassermodell dar. 3) Die elektrische Spannung der Batterie wird im Modell durch den unterschiedlichen Wasserstand in den Behältern dargestellt. Der Wasserdruck treibt die Wasserräder an. Der Wasserdruck wird am großem und am kleinen Wasserrad gemindert. Zeichne Druckmesser ein, die den äußeren Druck und den Druck an den Wasserrädern messen. 4) Stelle gegenüber und ergänze: Modell Bezeichnung Druck zwischen dem vollen und dem leeren Behälter Elektrischer Stromkreis Bezeichnung Größe Batteriespannung 12 V Größe 5 bar Druckunterschied durch das kleine Wasserrad Druckunterschied durch das große Wasserrad 5 bar Spannung am kleinen Widerstand 12 V 5 bar Spannung am großen Widerstand 12 V 5) Schalte die oben genannten Widerstände parallel und miss die Batteriespannung und die Spannungen an den Widerständen. R1 = 200 ; R2 = 100 1. UBatt = 12V U1 = 12V 2. UBatt = 9V U1 = 9V ; ; U2 = 12V U2 = 9V. 6) Sieh dir die Werte für die Batteriespannung und die Spannungen an den Widerständen an. Formuliere sprachlich und mathematisch ein Ergebnis. Die Batteriespannung ist genau so groß wie die Spannung an den Widerständen. 7) Prüfe die Spannungen an den Widerstanden bei folgen den Kombinationen: UBatt = 12V R1 = 100, R2 = 500 U1 = 12V; U2 =12V Was fällt dir auf? Formuliere den Zusammenhang schriftlich. Die Spannung an parallel geschalteten Widerständen ist nicht von deren Größe anhängig, sondern nur von der Größe der Batteriespannung. Ersatzwiderstand bei einer Parallelschaltung 1. Stelle eine Parallelschaltung zweier Widerstände verschiedener Größe im Wassermodell dar. voller Behälter leerer Behälter 2. Der elektrische Widerstand wird im Modell durch ...................................................... dargestellt. Die Wasserräder hemmen den Wasserstrom. Legt man zu einem Wasserweg einen Zweiten parallel, dann kann in der Zuleitung (mehr, weniger ) ................................................. Wasser fließen, folglich wird die Wasserhemmug ............................................................ (größer, kleiner). Will man die beiden Wasserräder durch ein einziges ersetzen, muss das Ersatzrad so beschaffen sein, das es den Wasserstrom in gleicher Stärke hemmt wie zwei Räder in Reihe. Gleiche Hemmung bedeutet: .......................................................................................................................................................................... ......................................................................................................................................................................... 3. Skizziere eine Parallelschaltung aus zwei Widerständen R1 = 200 und R2 = 100 mit einer Batterie. Zeichne ein Amperemeter zur Messung des Batteriestromes und ein Voltmeter zur Messung der Batteriespannung ein. 4. Schalte die genannten Widerstände parallel. Miss den Batteriestrom und die Batteriespannung. UBatt = 12V IBatt = ................. geschätzt: RParallel = ..................... 5. Ersetze in der Schaltung die Widerstände durch einen einzigen. Vergleiche dessen Größe mit den Werten der Einzelwiderstände. Formuliere sprachlich die Auffälligkeit. ............................................................................................................................................................................... 6. Der Ersatzwiderstand ist ein wirklicher Ersatz für die Einzelwiderstände, wenn ............................................ .............................................................................................................................................................................. 7. Den Ersatzwiderstand RParallel kann man berechnen, indem man die Batteriespannung durch den Batteriestrom teilt. Rechne für die Parallelschaltung R1 = 200 und R2 = 100 nach: UBatt = 12V, IBatt = .................. R Parallel UBatt IBatt Lösungen: Ersatzwiderstand bei einer Parallelschaltung 1. Stelle eine Parallelschaltung zweier Widerstände verschiedener Größe im Wassermodell dar. 2. Der elektrische Widerstand wird im Modell durch Wasserräder mi Lasten dargestellt. Die Wasserräder hemmen den Wasserstrom. Legt man zu einem Wasserweg einen zweiten parallel, dann kann in der Zuleitung (mehr, weniger ) mehr Wasser fließen, folglich wird die Wasserhemmug kleiner (größer, kleiner). Will man die beiden Wasserräder durch ein einziges ersetzen, muss das Ersatzrad so beschaffen sein, das es den Wasserstrom in gleicher Stärke hemmt wie zwei Räder in Reihe. Gleiche Hemmung bedeutet: Bei gleich starkem Wasserdruck muss ein gleich starker Wasserstrom fließen. 3. Skizziere eine Parallelschaltung aus zwei Widerständen R1 = 200 und R2 = 100 mit einer Batterie. Zeichne ein Amperemeter zur Messung des Batteriestromes und ein Voltmeter zur Messung der Batteriespannung ein. 4. Schalte die genannten Widerstände parallel. Miss den Batteriestrom und die Batteriespannung. UBatt = 12V IBatt = 18mA geschätzt: RParallel = 67Ω 5. Ersetze in der Schaltung die Widerstände durch einen einzigen. Vergleiche dessen Größe mit den Werten der Einzelwiderstände . Formuliere sprachlich die Auffälligkeit. Der Ersatzwiderstand ist kleiner als der kleinste Teilwiderstand. 6. Der Ersatzwiderstand ist ein wirklicher Ersatz für die Einzelwiderstände, wenn. bei gleich großer Spannung durch den Ersatzwiderstand ein gleich großer Strom fließt wie durch die Parallelschaltung. 7. Den Ersatzwiderstand RParallel kann man berechnen, indem man die Batteriespannung durch den Batteriestrom teilt. Rechne für die Parallelschaltung R1 = 200 und R2 = 100 nach: U 12000 mV UBatt = 12V, IBatt = 18mA IRe ihe Batt 67 IBatt 28mA Übungen zur Parallelschaltung 1. In einer Mehrfachsteckdose stecken die Stecker eines Radios, einer Lampe und eines Lüfters. Das Radio läuft. Was geschieht mit den Strömen durch die Geräte und die Stromstärke in der Zuleitung, wenn nacheinander die Lampe und der Lüfter eingeschaltet werden? 2. Skizziere für Aufgabe 1 das Schaltbild. Zeichne ein Amperemeter zur Messung der Gesamtstromstärke ein. 3. Wie ändert sich der Gesamtwiderstand, wenn zu einem Widerstand ein Zweiter parallel zugeschaltet wird? 4. Die Widerstände 10, 20 und 50 liegen parallel an einer Spannungsquelle. a. Durch welchen fließt der größte und durch welchen der kleinste Strom? b. Berechne den Gesamtwiderstand. 5. Die Spannungen an vier parallel geschalteten Widerständen sind zu bestimmen. Wie viele Messungen sind notwendig? 6. Parallelschaltung: UBatt = 9V, Gesucht: Rparallel, 7. Parallelschaltung: R1 = 15, Gesucht: Rparallel, 8. Parallelschaltung: I1 = 3mA, Gesucht: Rparallel, R1 = 300, R2 = 500 I1, IBatt I2, R2 = 18, IBatt = 122 mA I1, UBatt I2, R1 = 200, R2 = 40 UBatt, IBatt, I2 9. Fünf Widerstände von je 10 werden parallel geschaltet: Ersatzwiderstand? 10. Ermittle Spannungen und Ströme bei offenem und geschlossenem Schalter: a) UBatt = 12V, R1 = 30, R2 = 20, R3 = 40 b) UBatt = 10V, R1 = 28, R2 = 20, R3 = 30 Lösungen Blatt 1: Übungen zur Parallelschaltung 1. Die Stromstärke durch das Radio bleibt unverändert. In der Zuleitung addieren sich die Ströme von Radio, Lüfter und Lampe. Anders gesagt: Jedes Gerät „zieht“ seinen eigenen Strom aus dem Netz. Die Zuleitung muss also gleichzeitig alle Ströme verkraften. 2. 3. Der Gesamtwiderstand wird kleiner. In der Zuleitung fließt mehr Strom, also ist der Widerstand kleiner. 4. a. Durch den kleinsten Widerstand von 10 fließt der größte Strom. b. 1 R parallel 1 1 1 1 1 1 1 1 (0,1 0,05 0,02 ) 0,17 R1 R2 R3 10 20 50 Kehrwert beider Seiten bilden: R parallel 1 1 0,17 5,9 5. Eine Messung genügt, da alle Spannungen gleich groß sind. 6. Gegeben: UBatt = 9V, R1 = 300, 1 R parallel I1 1 1 1 1 R1 R2 300 500 U1 9V 0,03 A R1 300 7. Gegeben: R1 = 15, 1 R parallel I2 R2 = 18, 1 1 1 1 R1 R2 15 18 R2 = 500 Rparallel = 187,5 U2 9V 0,018 A R 2 500 IBatt = 122 mA Rparallel = 8,2 UBatt = Iparallel · Rparallel = 122mA · 8,2 = 1000mV = 1V I1 U1 1000 mV 67mA R1 15 8. Gegeben: I1 = 3mA, I2 = IBatt – I1 = 55mA R1 = 200, R2 = 40 UBatt = U2 = U1 = I1 · R1 = 3mA · 200 = 600mV I2 U2 600 mV 15mA R2 40 IBatt = I1 +I2 = 3mA + 15mA = 18mA = 0,018A Rparallel UBatt 600 mV 33,3 IBatt 18mA IBatt = I1 +I2 = 0,048A Lösungen Blatt 2: Übungen zur Parallelschaltung 9. 1 1 5 1 5 R parallel R 10 2 Rparallel = 2 10a. Offener Schalter: RReihe= R1 + R2 = 30 + 20 = 50, IRe ihe U1 = I1 · R1 = 0,24A · 30 = 7,2V UBatt 12 V 0,24 A , I1 = I2 = IReihe R Re ihe 50 U2 = UBatt – U1 = 12V – 7,2V = 4,8V 10a. Geschlossener Schalter: 1 R Schaltung I3 1 RRe ihe U3 12 V 0,3A R 2 40 1 1 1 R3 50 40 IRe ihe RSchaltung = 22,2 UBatt 12 V 0,24 A R Re ihe 50 U1 = I1 · R1 = 0,24A · 30 = 7,2V ISchaltung = IReihe +I3 = 0,54A U2 = UBatt – U1 = 12V – 7,2V = 4,8V 11b. Offener Schalter: RReihe= R1 + R2 = 28 + 20 = 48, IRe ihe U1 = I1 · R1 = 0,21A · 28 = 5,88V UBatt 10 V 0,21A , I1 = I2 = IReihe R Re ihe 48 U2 = UBatt – U1 = 10V – 5,88V = 4,12V 11b. Geschlossener Schalter: 1 1 1 1 1 Rpar R2 R3 20 30 Rparallel = 12 RSchaltung= R1 + Rparallel = 28 + 12 = 40 ISchaltung UBatt 10 V 0,25 A I1 = ISchaltung = 0,25A R Schaltung 40 U1 = I1 · R1 = 0,25A · 28 = 7V I2 Uparallel 3V 0,15 A R2 20 Uparallel = UBatt – U1 = 10V – 7V = 3V I3 = Iparallel – I2 = 0,25A - 0,15A = 0,1A Modell zur Reihenschaltung Gesetzmäßigkeiten der Reihenschaltung: Modell Elektrischer Stromkreis Ströme: Drücke: Ersatzwiderstand: Modell zur Parallelschaltung Gesetzmäßigkeiten der Parallelschaltung: Modell Drücke: Ströme: Ersatzwiderstand: Elektrischer Stromkreis Lösung: Modell zur Reihenschaltung Gesetzmäßigkeiten der Reihenschaltung: Modell Ströme: Die Wassermenge pro Sekunde, die aus dem vollen Behälter kommt, fließt auch durch beide Wasserräder und in den leeren Behälter Drücke: Der Druck, der durch den unterschiedlichen Wasserstand erzeugt wird, teilt sich auf die Wasserräder auf. Das Wasserrad mi der grossen Last baut den Druck stärker als das mit der kleinen Last. Ersatzwiderstand: Aus dem vollen Behälter fließt die gleiche Wassermenge, wenn am Ersatzrad eine Last hängt, die der Summe der Einzellast enspricht. Elektrischer Stromkreis IBatt = I1 = I2 UBatt = U1 + U2 RReihe = R1 + R2 Lösung: Modell zur Parallelschaltung G esetzmäßigkeiten der Parallelschaltung: Modell Drücke: Der Druck, der durch den unterschiedlichen Wasserstand Elektrischer Stromkreis UBatt = U1 = U2 erzeugt wird, wirkt auf beide Wasserräder in gleicher Größe. Ströme: Durch das Wasserrad mit der kleinen Last fließt mehr Wasser IBatt = I1 + I2 als durch das mit der großen Last. Die Wassermengen pro Sekunde, die die durch die parallelen Zweige fließt, addiere sich. Der Behälter muss die Wassermengen liefern. Ersatzwiderstand: Aus dem vollen Behälter fließt die gleiche 1 1 1 Wassermenge, wenn am Ersatzrad eine Last hängt, die kleiner ist als die R par R1 R2 kleinste Einzellast. . Test 1. Nenne die Gesetze, die für eine a) Reihenschaltung und b) Parallelschaltung gelten. 2. Eine Glühlampe hat folgende Daten: 130V/0,3A. Es steht jedoch nur eine Spannung von 220V zur Verfügung. Wie muss ein Widerstand geschaltet werden und wie groß muss er sein, damit man die Lampe betreiben kann? 3. Bei einem Kronleuchter sind 8 Lampen parallel geschaltet. Die Anschlussspannung beträgt 220V, und der Widerstand einer Lampe 600. Berechne: a) den Gesamtwiderstand, b) die Stromstärke in der Zuleitung c) die Größe des Stromes durch eine Lampe 4. Drei Widerstände (100 , 200 und 500 ) sollen a) parallel und b) hintereinander geschaltet werden. Berechne den jeweiligen Ersatzwiderstand. 5. Ein elektrischer Heizkörper enthält zwei gleich große Widerstände. Schalte die Widerstände so an Plus und Minus, dass bei Schaltstufe 1 der kleinste und bei Stufe 3 der größte Strom fließt aus der Batterie fließt. Stufe 1 6. Stufe 2 Was geschieht mit der Batteriespannung, dem Batteriestrom und dem Gesamtwiderstand, wenn der Schalter geschlossen wird? Begründe deine Aussagen! Stufe 3 Lösungen Blatt1: Test 1. Nenne die Gesetze, die für eine Parallelschaltung: Reihenschaltung: UBatt = U1 = U2 UBatt = U1 + U2 IBatt = I1 + I2 IBatt = I1 = I2 1 R Par 2. RReihe = R1 + R2 1 1 R1 R 2 Eine Glühlampe hat folgende Daten: 130V/0,3A. Es steht jedoch nur eine Spannung von 220V zur Verfügung. Wie muss ein Widerstand geschaltet werden und wie groß muss er sein, damit man die Lampe betreiben kann? Der Widerstand muss zur Glühlampe in Reihe geschaltet werden. UR = UBatt - ULampe UR = 220V – 130V = 90V U 90 V R R 300 IR 0,3A 3. 4. Bei einem Kronleuchter sind 8 Lampen parallel geschaltet. Die Anschlussspannung beträgt 220V, und der Widerstand einer Lampe 600. Berechne: a) den Gesamtwiderstand, b) die Stromstärke in der Zuleitung c) die Größe des Stromes durch eine Lampe c) I Lampe U Netz 220 V 0,37 A R Lampe 600 a) R Schalt UNetz 220 V 100 I Zuleit 2,2A b) IZuleit = 6 · Tlampe = 6 · 0,37 = 2,2A Drei Widerstände (100 , 200 und 500 ) sollen a) parallel und b) hintereinander geschaltet werden. Berechne den jeweiligen Ersatzwiderstand. Parallelschaltung Reihenschaltung 1 1 1 1 Rpar R1 R2 R3 Rreihe = R1 + R2 + R3 = 800Ω 1 1 1 1 Rpar 100 200 500 1 10 5 2 17 Rpar 1000 1000 1000 1000 Rpar 1000 59 17 Lösungen Blatt2: Test 5. Ein elektrischer Heizkörper enthält zwei gleich große Widerstände. Schalte die Widerstände so an Plus und Minus, dass bei Schaltstufe 1 der kleinste und bei Stufe 3 der größte Strom aus der Batterie fließt. 6. Stromstärke: Die Stromstärke in der Zuleitung wird größer. Zu dem bereits fließenden Strom durch die Reihenschaltung addiert sich der Strom durch den parallel geschalteten Widerstand. Gesamtwiderstand: Wenn ein Widerstand zu anderen parallel geschaltet wird, sinkt der Gesamtwiderstand der Schaltung. Batteriespannung: Sie ändert sich nicht, wenn der Widerstand groß ist.