Übung 1: Signale und Systeme

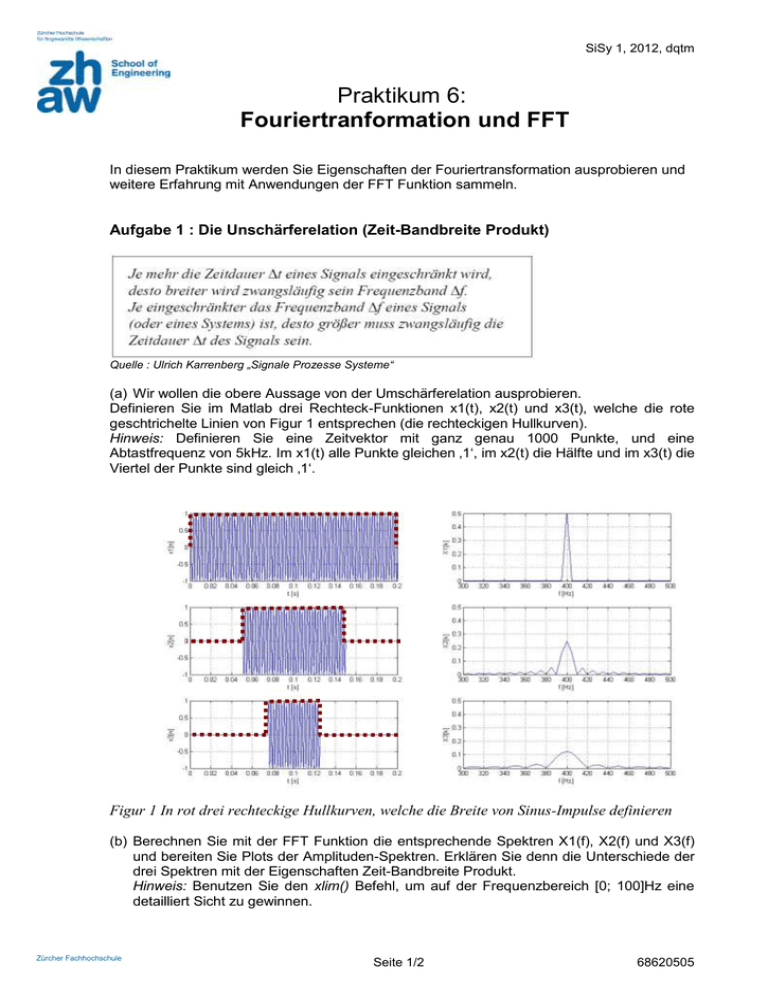
SiSy 1, 2012, dqtm
Praktikum 6:
Fouriertranformation und FFT
In diesem Praktikum werden Sie Eigenschaften der Fouriertransformation ausprobieren und
weitere Erfahrung mit Anwendungen der FFT Funktion sammeln.
Aufgabe 1 : Die Unschärferelation (Zeit-Bandbreite Produkt)
Quelle : Ulrich Karrenberg „Signale Prozesse Systeme“
(a) Wir wollen die obere Aussage von der Umschärferelation ausprobieren.
Definieren Sie im Matlab drei Rechteck-Funktionen x1(t), x2(t) und x3(t), welche die rote
geschtrichelte Linien von Figur 1 entsprechen (die rechteckigen Hullkurven).
Hinweis: Definieren Sie eine Zeitvektor mit ganz genau 1000 Punkte, und eine
Abtastfrequenz von 5kHz. Im x1(t) alle Punkte gleichen ‚1‘, im x2(t) die Hälfte und im x3(t) die
Viertel der Punkte sind gleich ‚1‘.
Figur 1 In rot drei rechteckige Hullkurven, welche die Breite von Sinus-Impulse definieren
(b) Berechnen Sie mit der FFT Funktion die entsprechende Spektren X1(f), X2(f) und X3(f)
und bereiten Sie Plots der Amplituden-Spektren. Erklären Sie denn die Unterschiede der
drei Spektren mit der Eigenschaften Zeit-Bandbreite Produkt.
Hinweis: Benutzen Sie den xlim() Befehl, um auf der Frequenzbereich [0; 100]Hz eine
detailliert Sicht zu gewinnen.
Zürcher Fachhochschule
Seite 1/2
68620505
SiSy 1, 2012, dqtm
Aufgabe 2 : Die Frequenz-Verschiebung und AM (Amplitudenmodulation)
(a) Definieren Sie jetzt die zeit-diskreten Funktionen y1(t), y2(t) und y3(t), welche die
Multiplikation von der drei Hullkurven mit einem Sinus mit Frequenz 400Hz entsprechen.
(b) Berechnen und ploten Sie jetzt die Spektren Y1(f), Y2(f) und Y3(f), und „zoomen“ Sie mit
xlim() auf dem „interessanten“ Teil des Frequenzbereich. Wo ist das jetzt? Benutzen Sie
die Frequenz-Verschiebung Eingenschaft, um die Unterschiede zwischen Xn(f) und Yn(f)
Spektren zu erklären.
(c) Wie ändern sich die Spektren, wenn Sie statt der rechteckigen Hullkurven drei langsam
Sinus mit Frequenz 5Hz, 10Hz und 20Hz als Hullkurven benutzen? Begründen Sie ihre
Antwort mit Plots im Matlab.
(d) Die Frequenz-Verschiebung Eingenschaft wird häufig benutzt für die Modulation von
einem Quelle-Signal auf einem Trägersignal. Erzeugen Sie jetzt mit den
Funktionsgenerator einem AM modulierten Signal, und beobachten Sie im Oszilloskope
mit der FFT Funktion das Spektrum des Signals.
Hinweis-1: Erzeugen Sie zuerst ein Sinus mit Frequenz 10kHz und Amplitude A = 2Vpp.
Addieren Sie die Modulation mit:
>Mod >Type AM >Done ; >Source >Internal ; >Depth > 100%;
>Freq > 1kHz; Shape >Sine
Hinweis-2: um eine stabileres Bild zu kriegen, verbinden Sie ihres Ausgangssignal an
channel-1, und das SyncOut an channel-2, und benutzen Sie channel-2 als Trigger.
(e) Können Sie besttätigen das dieses AM-Signal wird wie im Blockschalbild unten erzeugt?
Probieren Sie und erklären Sie den Einfluss des Parameters „m“ Depth (oder auf
Deutsch Modulationsgrad).
Aufgabe 3 : Dualität
(a) Erzeugen Sie mit dem Funktionsgenerator eine Pulse mit einem Sinc-Form, und
beobachten Sie dieses Signal im Zeit und Frequenzbereich mit der Oszilloskope.
Hinweis: Wählen Sie im Signal Generator >Arb >Load >BuiltIn1 > Sinc
(b) Benutzen Sie die Eigenschaft der Dualität um die Form des Spektrum zu erklären.
Aufgabe 4 Synthese eines Klanges.
In dieser Aufgabe probieren Sie einen gegebenen Klang zu synthetisieren Nehmen wir als
Beispiel den aufgezeichneten Klang in Glas.mat File, und führen Sie die folgenden Schritte
durch:
- Analysieren Sie mit DFT des gegebenen Sound-File (Referenz für gewünschten Klang);
- Bereiten Sie einen Plot in Zeit und Frequenz Bereich des Audio-Signal;
- Implementieren Sie im Matlab die vorgeschlagene Struktur für die Synthese:
Summe von dominanten Frequenzkomponenten gewichtet mit Hüllkurve;
Hinweis-1: Implementierung der Hüllkurve mit exp() Funktion oder impulse() von TPF;
Hinweis-2: Matlab Vorlage sisy1_prak6_auf4.m steht zur Verfügung.
Zürcher Fachhochschule
Seite 2/2
68620505