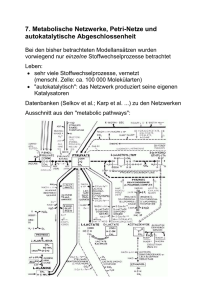
1.1. systeme mit anonymen marken

1 PETRI – NETZE
1.1. SYSTEME MIT ANONYMEN MARKEN
Ein Petri – Netz besteht aus zwei verschiedenen Sorten von Knoten,
( i ) Stellen, für die Ablage von Marken symbolisiert durch einen Kreis,
( ii ) Transitionen, für die Verarbeitung von Marken symbolisiert durch ein Rechteck.
Und den Elementen der Flußrelation den Kanten.
DEFINITION 1:
Ein Netzgraph N besteht aus den Komponenten S ( Menge der Stellen ), T ( Menge der Transitionen )
Und F ( Flußrelation ), kurz: N = (S,T,F) wobei gilt:
(i) S T = 
(ii) F  ( S  T )  ( T  S )
BEISPIEL 1:
t1
s2
t2
s3
s1
S = {s1,s2,s3} Menge der Stellen
T = {t1,t2}
Menge der Transitionen
DEFINITION 2:
Sei N = (S,T,F) ein Netz. Dann heißt N΄ = (S΄,T΄,F΄) Teilnetz von N
genau dann wenn
(i) S΄ S
(ii) T΄ T
(iii) F΄ F  (( S΄  T΄ )  ( T΄  S΄ ))
BEISPIEL 2:
t1
s1
t2
S΄= {s1}
T΄= {t1,t2} Die Kanten sind Elemente aus F  (( S΄  T΄ )  ( T΄  S΄ )).
Damit ist dieses Netz ein Teilnetz des Netzes aus Beispiel 1.
DEFINITION 3:
Ein Teilnetz bestehend aus einer Stelle s und einer Transition t, die doppelt verbunden sind heißt Schlinge.
BEISPIEL 3:
s1
t1
Im Zusammenhang mit einem Netzknoten x kann man zwei bestimmte Mengen von Nachbarknoten einführen:
(i) x  {y| (y,x)  F} , die Menge aller Eingangsknoten oder Vorbereich von x
(ii) x  {x| (x,y)  F} , die Menge aller Ausgangsknoten oder Nachbereich von x
Um die Dynamik von solchen Systemen darzustellen, führen wir nun weitere Begriffe ein.
DEFINITION 4:
Eine Struktur Y = (S,T,F,K,W,M₀) heißt Stellen-Transitionen-System bzw. S/T-System
genau dann wenn
(i) (S,T,F)
(ii) K: S    
(iii) W: F  
ein Netzgraph
Kapazität für Stellen
Kantengewichte
(iv) M₀: S  ₀
Anfangsmarkierung mit M₀ K(s) für alle s sind.
BEISPIEL 4:
Erdbeermilch



Erdbeeren
s1
Milch
s2

2
1
schneiden
t1


Zucker
s3
2
mixen
t2
5
geschnittene
Erdbeerren
s4
5
1
Erdbeermilch
s5
K(si) = 
Die folgenden Definitionen werden benutzt die Frage zu klären, wann und wie sich die Anfangsmarkierung
verändern läßt.
DEFINITION 5:
Man bezeichnet eine Transition t  T als aktiviert unter einer Markierung M
genau dann wenn
(i) s  t: M(s)  W(s,t)
(ii)s  t: M(s) + W(t,s)  K(s).
Schreibweise: M[t>
BEISPIEL 5:


nicht aktiviert

aktiviert
DEFINITION 6:
Man sagt t schaltet von M nach M‘ falls M[t> gilt und
M‘(s) =

M(s) – W(s,t) für s  t\t
M(s) + W(t,s) für s  t\t
M(s)  W(s,t) + W(t,s) für s  t  t
M(s) sonst
Schreibweise: M[t>M‘
BEISPIEL 6:
Erdbeermilch
Erdbeeren
s1


Milch
s2

2
1
schneiden
t1


2
mixen
t2
5
geschnittene
Erdbeerren
s4
Zucker
s3


5
1
Erdbeermilch
s5
DEFINITION 7:
Eine Schaltfolge M₀[t1...tn> steht für  Mi: M₀[t1>M₁[t2>...Mn-₁[tn>Mn .
DEFINITION 8:
Erreichbarkeitsmenge: [M₀> :={M‘:M₀[w>M‘, w  T*}
Dabei ist w ein Wort aus Transitionen, welches Element der Menge aller Wörter aus Transitionen T*
(incl. des leeren Wortes) ist.
ERREICHBARKEITSANALYSE:
(i) Zunächst wird die Anfangsmarkierung in die Erreichbarkeitstabelle eingetragen.
M₀ ist jetzt die aktuelle Markierung Mc.
Für Mc wird der Reihe nach jede Transition t darauf untersucht, ob sie aktiviert ist.
Wenn nein, sind wir momentan mit dieser Transition fertig.
Wenn ja, wird die Folgemarkierung zu Mc ermittelt.
- Ist die Folgemarkierung neu, wird sie als neue Markierung in die
Erreichbarkeitstabelle eingetragen.
- Ist sie bereits in der Erreichbarkeitstabelle vorhanden, so erfolgt kein neuer Eintrag.
(ii) Für die in (i) ermittelten Folgemarkierungen wird wie in (i) beschrieben verfahren, d.h. die
jeweilige Folgemarkierung ist die neue aktuelle Markierung Mc.
(iii) Sind alle in die Tabelle eingetragenen Markierungen nach dem in (i) beschriebenen
Verfahren untersucht, so ist man mit der Erreichbarkeitsanalyse abgeschlossen.
BEISPIEL 7:
Erreichbarkeitstabelle für Beispiel 4
ERREICHBARKEITSTABELLE
s1 s2 s3 s4 s5 Aktivierte Transitionen
M₀
6
3
6
0
0 M₀[t1>M₁
M₁
4
3
6
5
0 M₁[t1>M₂
M₁[t2>M₄
M₂
2
3
6 10
0 M₂[t1>M₃
M₂[t2>M₅
M₃
0
3
6 15
0 M₃[t2>M₆
M₄
4
2
4
0
1 M₄[t1>M₅
M₅
2
2
4
5
1 M₅[t1>M₆
M₆
0
2
4 10
1 M₆[t2>M₇
M₇
2
1
2
0
2 M₇[t1>M₈
M₈
0
1
2
5
2 M₈[t2>M₉
M₉
0
0
0
0
3
M₅[t2>M₇
DEFINITION 9:
Eine Liste von Transitionen ( d.h. eine Zusammenfassung, ggf. mit Wiederholungen )
T = [t1, ... ,tn] heißt „nebenläufig aktiviert“ unter einer Markierung M, falls alle Permutationen von T unter M
als Schaltfolgen aktiviert sind. Aufgrund der Ergebnisinvarianz bei Umordnung können wir schreiben:
M[[t1,...,tn]>M‘ mit eindeutig bestimmtem M‘
BEISPIEL 8:
s1
t1
s2

t2
t3
s3
s4
In diesem Beispiel zeigt sich, dass aus paarweiser Nebenläufigkeit (von t1,...,t3) nicht auf
Nebenläufigkeit von[t1,t2,t3] geschlossen werden kann.
Daraus ergibt sich folgendes Problem:

Geld
Disco gehen
Klamotten kaufen
Für eine beschränkte Menge Geld läßt sich nur ein Wunsch verwirklichen.
Dieses nennt man Konflikt.
Konflikt
Als Konflikt wird eine nicht-nebenläufige Aktivierung mehrerer Transitionen bezeichnet.
Die Frage ist: Wie lassen sich solche Probleme innerhalb von Petri – Netzen lösen.?
Lust

Geld
Disco gehen

keine Lust
Klamotten kaufen
Die Konfliktbeseitigung ist durch Einführung von zusätzlichen Eingabestellen möglich geworden.
1.2.Bedingungs-Ereignis-System
Bedingungs-Ereignis-Systeme sind Systeme, deren Stellen entweder eine Marke tragen (Bedingung gilt) oder
unmarkiert sind (Bedingung gilt nicht).
Aus diesem Grunde fordern wir generell die Stellenkapazität 1, denn eine Bedingung kann normalerweise nicht
mehrfach gelten.
Daraus folgt, dass die Kantengewichte auch nicht größer als 1 sein dürfen und dass Schleifen keinen Sinn
machen. Für ein B/E- System fordern wir zusätzlich, dass es keine zwei Bedingungen gibt, die durch dieselben
Ereignisse eintreten und durch dieselben Ereignisse beendet werden, und es gibt keine zwei Ereignisse, die
dieselben Bedingungen herbeiführen und dieselben Bedingungen beenden. Dieses bedeutet aber nichts anderes
als die Schlichtheit des Netzes.
DEFINITION 10:
Ein B/E-System ist ein S/T- System mit schlingenfreiem, schlichtem Netz. Außerdem müssen alle
Stellenkapazitäten und alle Kantengewichte gleich 1 sein.
Das Problem des Konfliktes tritt auch bei B/E – Systemen auf.
Konflikt
Unter einem Konflikt versteht man die wechselseitige eingabeseitige Behinderung von Transitionen.
Es ergibt sich nicht nur auf der Eingabeseite ein Problem, sondern auch auf der Ausgabeseite.
Kontakt
Unter einem Kontakt versteht man die wechselseitige ausgabeseitige Behinderung von Transitionen.
1.3. Netze mit individuellen Marken
Beispiele für Netze mit individuellen Marken:






Prädikat-Transitions-Netze
Produktnetze
Coloured Nets
Relationennetze
Predicate-Event Nets
P-Nets
BEISPIEL 9:
4
s1
T1
x1
x1 > x2
x2 = x3
x4 = x1 – x2
x4
s2
1 3
1 3
s3
x3 x2
Stellen:
wohldefinierte (mathematische) Objekte
Transitionen: 1. Es beschreibt eine inhaltliche Forderungen an die gegebenenfalls zu entnehmenden Marken,
ohne deren Erfüllung die Transition nicht schalten soll.
2. Es beschreibt Bedingungen an die gegebenenfalls abzulegenden Marken, meist in
Abhängigkeit von den entnommenen Marken. In praktischen Anwendungen werden
die Outputmarken durch diese Bedingungen im allgemeinen eindeutig definiert.
Kanten:
quantitative Anschriften mit Variablennamen
Schaltungen: Variablenbelegung