m``(s)

Petrinetze
1. Einführung
Informatik : wesentlich Modellierung von
Struktur und Verhalten realer oder virtueller
Systeme
Systeme: Netze aus Personen, Geräten, Prozessoren,
die miteinander kooperieren oder konkurrieren
Modellierungshilfsmittel: formal
anschaulich
Petrinetze: sehr beliebt bei Anwendern, insbes. Ingenieuren
Einführendes Beispiel
(Reisig/Rozenberg: Informal Introduction to Petri Nets, LNCS 1491, SS 1 - 11)
2. Anschauliche Erläuterung des Konzepts der Petrinetze
Intuitive Bedeutung von
Ellipse (oder Kreis): passive Komponente (Speicher; Bedingung,
(Stelle/place)
die erfüllt oder nicht erfüllt sein kann;
lokale Zustandskomponente;
sie bewahrt auf, macht zugreifbar/sichtbar)
Rechteck (oder Quadrat):
(Transition)
aktive Komponente
(Prozessor, Mensch, Ereignis;
sie erzeugt, transportiert, ändert)
Pfeil:
repräsentiert nicht eine Systemkomponente
sondern ist Mittel der Beschreibung für
Zusammenhang/Beziehung, Zugriffsmöglichkeit/-recht,
physikalische Nähe, direkte Verbindung.
Verbindet nur Komponenten verschiedenen Typs
(passiv-aktiv, aktiv-passiv)
Bisher nur "Bilder", statische Ansichten / Schnappschüsse
Wie wird Dynamik / werden Abläufe / Zustandsänderungen
dargestellt?
Zustandsänderung
im System bewirkt durch Ereignis/Aktivität
im Petrinetz durch "Schalten" von Transitionen
Was ist "der aktuelle Zustand" ?
Im System: der relevante Speicherinhalt,
das Erfüllt- oder Nichterfülltsein der relevanten
Bedingungen,...
Zustandsinformation für eine aktive Komponente
ist stets lokal.
Im Petrinetz: Die Inhalte ("Markierungen") der Stellen.
Der relevante (lokale) Zustand für eine Transition
ist bestimmt durch die mit der Transition
durch Pfeile verbundenen Stellen
Einfachste Art der Markierung:
Schwarze Punkte
(„Marken“, token)
# zunächst werden nur solche Markierungen betrachtet #
+ eine Marke in einer Stelle kann z.B. das Erfülltsein
einer Bedingung bedeuten
+ mehrere Marken bedeuten z.B. einen Vorrat an Ressourcen,
die zum Schalten benötigt werden
Was passiert beim Schalten einer Transition?
Nur relevante lokale Zustände werden berücksichtigt/verändert:
Schalten der Transition t: Entlang jedes mit t verbundenen Pfeiles
wird in Pfeilrichtung eine Marke transportiert
- von einer Stelle weggenommen oder auf sie gelegt.
Also Voraussetzung fürs Schalten von t: Es müssen genügend
Marken (in jeder mit t verbundenen Stelle)
vorhanden sein: t muß "aktiviert" sein
Schalten einer Transition
3. Grundlegende Definitionen
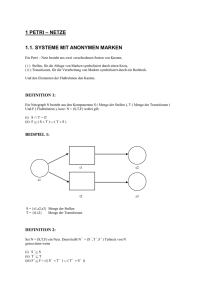
Netz N = ( S, T, F )
Stellen
Transitionen
•x = {y  N | (y,x)  F}
analog
x• = {y ... | (x,y) ...}
ST =
F  (S  T)  (T  S)
Flußrelation, Pfeile
, •X = {•x | x  X }
, X• = ... x•
Markierung: Abbildung m : S –––––> |N = { 0,1,2,3, ... }
Stelle s aus S heißt markiert, wenn m(s) > 0
------------Transition t heißt aktiviert, wenn alle Stellen aus •t markiert sind.
Dann kann t schalten,
d.h. die Markierung von •t  t•
m(s) -1
m´(s) =
{
m(s) + 1
m(s)
Man schreibt auch m[t > m´
Äquivalent ist
so ändern:
für s aus •t - t•
für s aus t• - •t
sonst
m´(s) = m(s) - | F  {(s,t)} | + | F  {(t,s)} |
---------------------
Markierung m heißt tot, wenn sie keine Transition aktiviert
Sei m eine Markierung des Netzes N = (S,T,F).
Eine Folge t1 , t2 , ... ,tk von Transitionen von N heißt
bei m aktivierte Schaltfolge, wenn k = 0 oder wenn
m[t1 > m1 und t2 , ...,tk bei m1 aktiviert ist.
Mit  = 
m[ > m
bzw.
bzw.
 = t1 t2 ... tk
gelte
m[ > mk , wobei m1 [t2 .... tk > mk
Feststellung:
* Aus m[ > m´ und l[ > l´ folgt für jede Stelle s aus S
m´(s) - m(s) = l´(s) - l(s)
* Seien m, l Markierungen mit m(s) >= l(s) für jedes s aus S,
dann ist jede bei l aktivierte Schaltfolge auch bei m aktiviert.
* Seien u, v aus T mit v•  •u = , dann gilt
mit m[vu > m´ auch m[uv > m´.
Eigenschaften markierter Netze
Markiertes Netz (Netzsystem): (N,m)
Netz N mit (Anfangs)markierung m
Markierung m´ heißt erreichbar in (N,m), wenn es eine
bei m aktivierte Schaltfolge  mit m[ > m´ gibt.
Stelle s von (N,m) heißt beschränkt, wenn nat. Zahl b existiert
mit m´(s) <= b für jede erreichbare Markierung von (N,m).
Mark. Netz heißt beschränkt, wenn jede Stelle beschränkt
Bemerkung: Bei beschränkten Netzen kann die Zahl der
erreichb. Markierungen exponentiell mit der Netzgröße wachsen
Satz: Für endliche mark. Netze ist Beschränktheit entscheidbar
Markierungsgraph eines markierten Netzes
• Knoten ~ alle erreichbaren Markierungen
Startknoten ~ Anfangsmarkierung
• Pfeil mit Transitionsbezeichner t
von Knoten (Markierung) m zu Knoten m’
g.d., w. t bei m aktiviert und m[t>m’
- endlich g.d., w. markiertes Netz beschränkt
- markiertes Netz ist verklemmungsfrei g.d.,w. von jedem Knoten des
Markierungsgraphen mindestens ein Pfeil wegführt.
Transition t heißt tot bei der Markierung m, wenn sie bei
keiner von m aus erreichbaren Markierung aktiviert ist.
Ein markiertes Netz heißt lebendig, wenn bei keiner
erreichbaren Markierung eine Transition tot ist
Ein mark. Netz heißt verklemmungsfrei (schwach lebendig),
wenn keine erreichbare Markierung tot ist.
Ein mark. Netz heißt reversibel, wenn seine Anfangsmarkierung
von jeder anderen erreichbaren Markierung erreichbar ist.
Überdeckungsgraph eines markierten Netzes (N, m )
0
Für unbeschränkte markierte Netze statt Markierungsgraph eine
reduzierte endliche Darstellung
Knoten ~ verallgemeinerte Markierungen m
Konstruktion analog zu der eines Markierungsgraphen
• Start mit Anfangsmarkierung
• sukzessive Pfeile von Knoten m zu Knoten m’, wenn m[t> m’,
aber
wenn auf Weg von m zu m’ schon ein m’’ auftrat mit
m’(s)≥ m’’(s) für alle s,
dann setze m’(s’) =  für alle s’ mit m’(s’)> m’’(s’)
0
m’(s’) =  bedeutet, daß s’ unbeschränkt ist, (und mindestens, eine
Marke enthält). Denn von m’ aus kann man dieselbe Schaltfolge
ablaufen lassen, die von m’’ zu m’ führte, und so die Markenzahl wieder
echt vergrößern usw.
Satz: (N, m) ist beschränkt g.d., w. bei der Konstruktion des
Überdeckungs-Graphen kein  auftritt.