Übungen zur Vorlesung Klassische Mechanik WS 2003/04 Prof. Dr
Werbung

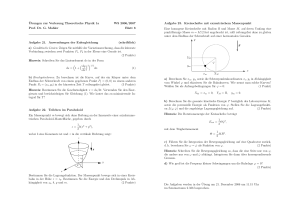
Übungen zur Vorlesung Klassische Mechanik WS 2003/04 Prof. Dr. G. Mahler Blatt 12 c) Führen Sie die Integration der Bewegungsgleichung auf eine Quadratur zurück, d. h. berechnen Sie ω = ϕ̇ als Funktion von ϕ. (2 Punkte) Hinweis: Schreiben Sie die Bewegungsgleichung so, dass die eine Seite nur von ϕ, die andere nur von ω und ω̇ abhängt. Integrieren Sie dann über korrespondierende Grenzen. Aufgabe 48. Kontrollfragen d) Wie groß ist die Frequenz kleiner Schwingungen um die Ruhelage ϕ = 0? (2 Punkte) a) Was besagt der Steinersche Satz? b) Wie kommt man vom Drehimpulssatz zur Kreiselgleichung? e) Berechnen Sie die von der Unterlage auf den Körper (Scheibe und Massenpunkt) ausgeübte Zwangskraft Z(ϕ, ϕ̇, ϕ̈). Bestimmen Sie dazu die Bewegungsgleichungen in kartesischen Koordinaten. (3 Punkte) c) Was gilt speziell für den kräftefreien Kugelkreisel? d) Was versteht man unter Nutation bzw. Präzession? Aufgabe 49. Kreisscheibe mit exzentrischem Massenpunkt Eine homogene Kreisscheibe mit Radius R und Masse M auf deren Umfang eine punktförmige Masse m = M2 fest angebracht ist, rollt reibungsfrei ohne zu gleiten unter dem Einfluss der Schwerkraft auf einer horizontalen Geraden. y PSfrag replacements f ) Bei hinreichend großer Anfangsgeschwindigkeit v = ẊM kann die Kreisscheibe infolge ihrer (durch den Massenpunkt m bewirkten) Unwucht hochspringen. Welche Bedingung muss zu Beginn des Hochspringens erfüllt sein? (1 Punkt) g) Wie groß muss die Anfangsgeschwindigkeit sein, damit der Abspringvorgang bei ϕ = (2π)/3 beginnt? (2 Punkte) h) In welcher Position springt die Kreisscheibe hoch, wenn v 2 À gR ist, d. h. wenn gR gegenüber v 2 vernachlässigt werden darf? (1 Punkt) g Aufgabe 50. Gleitende Kugel YM ϕ ym x XM xm a) Berechnen Sie xm , ym sowie die Schwerpunktskoordinaten xs , ys in Abhängigkeit vom Winkel ϕ und skizzieren Sie die Bahnkurven. Wie nennt man solche Kurven? Wählen Sie als Anfangsbedingungen für ϕ = 0: (1 Punkt) XM = xm = 0, YM = R, ym = 0. b) Berechnen Sie die gesamte kinetische Energie T bezüglich des Laborsystems K, sowie die potenzielle Energie als Funktion von ϕ. Stellen Sie die Lagrangefunktion L(ϕ, ϕ̇) und die zugehörige Lagrangegleichung auf. (2 Punkte) Hinweis: Die Rotationsenergie der Kreisscheibe beträgt Erot 1 = Θϕ̇2 , 2 mit dem Trägheitsmoment Θ= 1 M R2 . 2 (schriftlich) a) Berechnen Sie das Trägheitsmoment Θ einer Kugelschale mit gegebenem Außenund Innenradius (Ra und Ri ) bezüglich einer Drehachse durch den Mittelpunkt für den Fall homogener Massenverteilung innerhalb der Schale. Was ergibt sich für die (1 Punkt) Grenzfälle Ri → Ra und Ri = 0? b) Die Kugelschale wird im homogenen Gravitationsfeld auf eine horizontale Unterlage gesetzt und durch einen Kraftstoß auf die Anfangsgeschwindigkeit v 0 gebracht ohne zu rotieren. Die Gleitreibungszahl zwischen Kugelmaterial und Untergrund sei µG . Stellen Sie die Bewegungsgleichungen für die Translations- und Rotationsbewegung auf und lösen Sie diese unter der gegebenen Anfangsbedingung. Nach welcher Zeit geht die Gleitbewegung in eine Rollbewegung über? Wie groß ist die Geschwindigkeit der Kugel zu diesem Zeitpunkt (Formel für Θ nicht einsetzen!)? (2 Punkte) c) Welcher Bruchteil der Anfangsenergie wurde während der Gleitphase der Bewegung von der Reibung aufgezehrt? Welches Ergebnis erhält man für einen Fuß(1 Punkt) ball (Ri → Ra ) und eine Billardkugel (Ri = 0)? d) Gibt es für diese Bewegung trotz vorhandener Reibung einen Erhaltungssatz? Können Sie daraus die erreichte Geschwindigkeit der Kugel errechnen? (1 Punkt)