10 6 Ueb Elektrotechnik

STR – ING
Elektrotechnik
10 - 6 - 1
_____________________________________________________________________
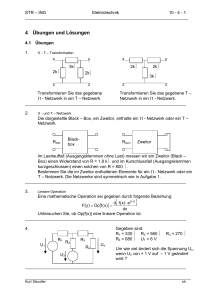
6 Übungen und Lösungen
6.1
1.
Übungen
EINTORE
R
A
B
B
C
R
B
L
R
A
A
C
L
A
B
R
Z AB
für
R
die vier dargestellten Eintore mit den Normierungen Ω = ω ⋅ RC beziehungsweise
L
Ω = ω⋅ .
R
Stellen Sie das Impedanzverhalten (Betrag)
auf doppeltlogarithmischem Papier dar.
Stellen Sie das Winkelverhalten (Phase) ϕ(ω)
auf einfachlogarithmischem Papier dar.
Suchen Sie das Impedanzverhalten
____________________________________________________________________
2.
EINTOR
P
R
C
Q
Es sind R = 56 kΩ und C = 22 nF.
Bei welcher Frequenz f wird |ZPQ| = 100 kΩ ?
Wie gross wird ϕ an dieser Stelle ?
____________________________________________________________________
Gegeben sei die nebenstehende Parallelschaltung mit R = 2,7 kΩ und L = 16 mH.
a)
Wie gross wird die Impedanz |ZAB| bei eiL
ner Frequenz von f1 = 12 kHz ?
A
B
b) Wie gross wird der Phasenwinkel ϕ1 an
dieser Stelle ? Zeigerdarstellung ?
R
R
c) Bei welcher Frequenz f2 wird |ZAB|=
?
2
d) Wie gross wird ϕ2 in c) ?
____________________________________________________________________
3.
EINTOR
Gegeben sei die nebenstehende Schaltung
mit R1 = 33 kΩ, C = 8,2 nF und R2 = k⋅R1.
C
R2
a) Wie gross wird die Impedanz |ZXY| bei eiY
X
R1
ner Frequenz von f1 = 800 Hz und aa) k =
1, ab) k = 0,1, ac) k = 10 ?
b) Wie gross wird der Phasenwinkel ϕ1 an
diesen Stellen ki ? Zeigerdarstellungen ?
c) Stellen Sie das Impedanzverhalten
|ZXY|(Ω) mit Ω = ω ⋅ R1C grafisch dar.
____________________________________________________________________
4.
EINTOR
______________________________________________________________________
Kurt Steudler
str
STR – ING
Elektrotechnik
10 - 6 - 2
_____________________________________________________________________
5.
EINTOR
C
A
2C
B
R
2
R
Wie gross werden die Impedanz |ZAB|1 und
der Phasenwinkel ϕ1 ?
R = 39 kΩ , C = 1,8 nF , f1 = 2,3 kHz
Für welche Frequenz f2 wird |ZAB|2 = 47 kΩ
gross ? Phasenwinkel ϕ2 ?
____________________________________________________________________
R1 = 100 Ω, C = 10 nF
R2 = 220 Ω, L = 300 µH, ω = 1,6 105 s-1
R1
C
A
B
Bestimmen Sie die beiden Impedanzen ZAB
L
und ZXY formal und in Zahlen.
R2
X
Y
Geben Sie die Zeigerdarstellungen an für ZAB,
ZXY und ZAB + ZXY .
Welchen Wert haben der Betrag und der
Winkel von ZAB + ZXY ?
____________________________________________________________________
6.
EINTORE
R1 = 270 Ω, C = 12 nF
R2 = 120 Ω, L = 500 µH, f = 120 kHz
R1
C
A
B
Bestimmen Sie die beiden Impedanzen ZAB
L
und ZXY formal und in Zahlen.
R2
X
Y
Geben Sie die Zeigerdarstellungen an für ZAB,
ZXY und ZAB // ZXY (Parallelschaltung).
Welchen Wert haben der Betrag und der
Winkel von ZAB // ZXY ?
____________________________________________________________________
7.
EINTORE
8.
BEWEISFÜHRUNG
XP
Zeigen Sie, dass gilt
RS
•
RP
für
=
LP
LS
ZAB
ϕ
XS
RP
RS
____________________________________________________________________
______________________________________________________________________
Kurt Steudler
str
STR – ING
Elektrotechnik
10 - 6 - 3
_____________________________________________________________________
9.
Zeigen Sie, dass gilt
BEWEISFÜHRUNG
XP
RS
•
RP
für
ZAB
=
CP
XS
CS
ϕ
RP
RS
____________________________________________________________________
10.
ZWEITOR
ue(t) = û sin(ωt - π/6)
L1 = 200 µH, L2 = 400 µH
L1
ue(t)
L2
ua(t)
Bestimmen Sie ua(t).
____________________________________________________________________
11.
ZWEITOR
ue(t) = û sin(ωt - π/4)
C1 = 20 nF, C2 = 40 nF
C1
ue(t)
C2
ua(t)
Bestimmen Sie ua(t).
____________________________________________________________________
12.
ZWEITOR
L
ue(t)
mit Ω = ω
R
L
.
R
u
Stellen Sie 20 ⋅ lg a
 ue
ua(t)

 = dB
ua und


u
e
ϕ  u  (Ω ) grafisch dar (einfachlogarithmia
Bestimmen Sie
ua
ua
(Ω )
(Ω )
ue
ue
 
 ue 
ϕ  u  (Ω )
a
 
 ue 
sches Papier).
Bestimmen Sie die Eckfrequenz ΩEck und Ω0
für |ϕ | = π/4.
____________________________________________________________________
______________________________________________________________________
Kurt Steudler
str
STR – ING
Elektrotechnik
10 - 6 - 4
_____________________________________________________________________
13.
ZWEITOR
mit Ω = ωR1C und k =
R1
ue(t) R2
C
ua(t)
u
Stellen Sie 20 ⋅ lg a
 ue
R2
.
R1

 = dB
ua und


u
e
ϕ  u  (Ω ) grafisch dar (einfachlogarithmia
 
 ue 
Bestimmen Sie
ua
ua
(Ω )
(Ω )
ue
ue
ϕ  u  (Ω )
a
 
 ue 
sches Papier).
Bestimmen Sie die Eckfrequenz ΩEck und Ω0
für |ϕ | = π/4.
____________________________________________________________________
14.
ZWEITOR
mit Ω = ωR 2C und k =
u
Stellen Sie 20 ⋅ lg a
 ue
R1
C
ue(t) R2
R1
.
R2

 = dB
ua und


u
e
ϕ  u  (Ω ) grafisch dar (einfachlogarithmia
ua(t)
 
 ue 
Bestimmen Sie
ua
ua
(Ω )
(Ω )
ue
ue
ϕ  u  (Ω )
a
sches Papier).
Bestimmen Sie die Eckfrequenz ΩEck und Ω0
für |ϕ | = π/4.
 
 ue 
____________________________________________________________________
15.
ZWEITOR
R1
mit Ω = ω
L
ue(t)
Bestimmen Sie
ua
ua
(Ω )
(Ω )
ue
ue
R2
ua(t)
R
L
und k = 1 .
R2
R2
u
Stellen Sie 20 ⋅ lg a
 ue

 = dB
ua und


u
e
ϕ  u  (Ω ) grafisch dar (einfachlogarithmia
 
 ue 
ϕ  u  (Ω )
a
 
 ue 
sches Papier).
Bestimmen Sie die Eckfrequenz ΩEck und Ω0
für |ϕ | = π/4.
____________________________________________________________________
______________________________________________________________________
Kurt Steudler
str
STR – ING
Elektrotechnik
10 - 6 - 5
_____________________________________________________________________
16.
ZWEITOR
R1
ue(t)
mit Ω = ω
R
L
und k = 2 .
R1
R1
u
Stellen Sie 20 ⋅ lg a
 ue
L
ua(t)

 = dB
ua und


u
e
ϕ  u  (Ω ) grafisch dar (einfachlogarithmia
R2
 
 ue 
Bestimmen Sie
ua
ua
(Ω )
(Ω )
ue
ue
ϕ  u  (Ω )
a
sches Papier).
Bestimmen Sie die Eckfrequenz ΩEck und Ω0
für |ϕ | = π/4.
 
 ue 
____________________________________________________________________
17.
ZWEITOR
R1
mit Ω = ωR1C und k =
u
Stellen Sie 20 ⋅ lg a
 ue
R2
ue(t)
ua(t)
C
Bestimmen Sie
ua
ua
(Ω )
(Ω )
ue
ue
R2
.
R1

 = dB
ua und


u
e
ϕ  u  (Ω ) grafisch dar (einfachlogarithmia
 
 ue 
ϕ  u  (Ω )
a
 
 ue 
sches Papier).
Bestimmen Sie die Eckfrequenzen ΩEck und
Ω0 für |ϕ | = π/4.
____________________________________________________________________
18.
ZWEITOR
R1
R2
ue(t)
Bestimmen Sie
ua
ua
(Ω )
(Ω )
ue
ue
mit Ω = ω
L
ua
R
L
und k = 2 .
R1
R1
u
Stellen Sie 20 ⋅ lg a
 ue

 = dB
ua und


u
e
ϕ  u  (Ω ) grafisch dar (einfachlogarithmia
 
 ue 
ϕ  u  (Ω )
a
 
 ue 
sches Papier).
Bestimmen Sie die Eckfrequenzen ΩEck und
Ω0 für |ϕ | = π/4.
____________________________________________________________________
______________________________________________________________________
Kurt Steudler
str
STR – ING
Elektrotechnik
10 - 6 - 6
_____________________________________________________________________
Auf welcher Frequenz f0 ist der gegebene Serieschwingkreis resonant ? Was bedeutet hier
Resonanz ?
R
L
C
B
Wie gross ist die Güte QSU ?
A
Bestimmen Sie die Bandbreite B in Hertz und
normiert. Wo liegen die Grenz- oder Eckfrequenzen f1 und f2 ?
R = 560 mΩ, C = 330 pF, L = 100 µH
____________________________________________________________________
19.
SCHWINGKREIS
20.
SCHWINGKREIS
R
L
C
A
B
Auf welcher Frequenz f0 ist der gegebene Serieschwingkreis resonant ?
Welchen Wert hat der Widerstand R ?
Bestimmen Sie die Bandbreite B in Hertz und
normiert. Wo liegen die Grenz- oder Eckfrequenzen f1 und f2 ?
QSU = 150, C = 100 pF, L = 330 µH
____________________________________________________________________
21.
Bestimmen Sie
SCHWINGKREIS
R
L
A
ua
(Ω )
ue
C
ua
(Ω )
ue
B
C
Ω = ω LC , kΩ = ω
R = 2 Ω, C = 820 pF, L = 200 µH
ϕ  u  (Ω ) mit
a
 
 ue 
1
L
und Ω = ωRC .
k
R
Stellen Sie |ZAB|/R grafisch dar. Bei welchen Frequenzen wird |ZAB| maximal oder minimal ?
____________________________________________________________________
22.
ZWEITOR
SCHWINGKREIS
Ri
ue
L
R
ua
u
Wie verläuft a (Ω ) am nebenstehende Zweiue
tor ?
Analysieren Sie das Zweitor.
RL
C
Bestimmen Sie die Notchbreite BN in Hertz
und die Notchtiefe AN in dB.
RL = Ri = 75 Ω, C = 12 nF, L = 50 µH, QSU = 300
____________________________________________________________________
______________________________________________________________________
Kurt Steudler
str
STR – ING
Elektrotechnik
10 - 6 - 7
_____________________________________________________________________
23.
ZWEITOR
SCHWINGKREIS
Ri
R
L
u
Wie verläuft a (Ω ) am nebenstehende Zweiue
tor ?
Analysieren Sie das Zweitor.
C
RL
Bestimmen Sie die Durchlassfrequenz f0, die
Bandbreite B und die Grenzfrequenzen f1 und
f2.
Wie gross wird die Güte QSL ? Welchen Wert
RL = Ri = 50 Ω, C = 1,2 nF, L = 500 µH, QSU = 300 nimmt die Einfügungsdämpfung A in dB an ?
____________________________________________________________________
ue
24.
SCHWINGKREIS
R
A
L
B
C
ua
Auf welcher Frequenz f0 ist der gegebene Parallelschwingkreis resonant ? Was bedeutet
hier Resonanz ?
Wie gross ist die Güte QPU ?
Bestimmen Sie die Bandbreite B in Hertz und
normiert. Wo liegen die Grenz- oder Eckfrequenzen f1 und f2 ?
R = 2,7 Ω, C = 3,3 nF, L = 200 µH
____________________________________________________________________
25.
Im nebenstehenden Zweitor seien
R = 82 Ω, C = 1 nF, L = 640 µH und p = 100
ZWEITOR
L
pR
R
ue(t)
ua(t)
C
a) Skizzieren Sie den Amplituden- und den
Phasengang, sowie die Ortskurve.
b) Bei welcher Frequenz f1 werden A = - 3dB
erreicht ?
c) Für welche Frequenz f2 wird |ϕ2| = π/2.
Wie gross wird hier die Dämpfung ?
____________________________________________________________________
R1 = 2⋅R, R2 = 5⋅R, L1 = 5⋅L, L2 = 2⋅L
L
Normierung: Ω = ω
R
R1
L2
a) Skizzieren Sie den Amplituden- und den
Phasengang, sowie die Ortskurve.
L1 R2
ue
ua
b) Stellen Sie das geordnete Gleichungssystem aus einem Knotenansatz auf.
c) Analysieren Sie ua/ue.
____________________________________________________________________
26.
ZWEITOR
______________________________________________________________________
Kurt Steudler
str
STR – ING
Elektrotechnik
10 - 6 - 8
_____________________________________________________________________
27.
ZWEITOR
p = 0,1, q = 10, Ω = ωRC
C
pR
R
ue(t)
u
ua(t)
qC
a) Skizzieren Sie den Amplituden- und den
Phasengang, sowie die Ortskurve.
b) Stellen Sie das geordnete Gleichungssystem aus einem Knotenansatz auf.
c) Analysieren Sie ua/ue.
____________________________________________________________________
28.
ZWEITOR
Ω = ω LC , kΩ = ω
L
pR
1
L
und Ω = ωRC .
k
R
a) Skizzieren Sie den Amplituden- und den
Phasengang, sowie die Ortskurve.
R
ue(t)
ua(t)
C
b) Analysieren Sie ua/ue.
____________________________________________________________________
29.
Bestimmen Sie
ua
ua
(Ω )
(Ω )
ue
ue
ZWEITOR
R
C
q
C
ue(t)
qR
ua
ϕ  u  (Ω )
a
 
 ue 
Bestimmen Sie die Eckfrequenzen, Grenzfrequenzen oder 3dB-Orte.
Für welche Frequenz(en) fi wird |ϕi| = π/4 ?
Für welche Frequenz wird |ϕ | maximal ?
____________________________________________________________________
30.
Bestimmen Sie
ua
ua
(Ω )
(Ω )
ue
ue
ZWEITOR
R
ue(t)
C
C
R
ua
ϕ  u  (Ω )
a
 
 ue 
Bestimmen Sie die Eckfrequenzen, Grenzfrequenzen oder 3dB-Orte.
Für welche Frequenz(en) fi wird |ϕi| = π/4 ?
Für welche Frequenz wird |ϕ | maximal ?
____________________________________________________________________
______________________________________________________________________
Kurt Steudler
str
STR – ING
Elektrotechnik
10 - 6 - 9
_____________________________________________________________________
31.
Bestimmen Sie
ua
ua
(Ω )
(Ω )
ue
ue
ZWEITOR
C
ue(t)
2R
2C
R
ua
ϕ  u  (Ω )
a
 
 ue 
Bestimmen Sie die Eckfrequenzen, Grenzfrequenzen oder 3dB-Orte.
Für welche Frequenz(en) fi wird |ϕi| = π/4 ?
Für welche Frequenz wird |ϕ | maximal ?
____________________________________________________________________
32.
Bestimmen Sie
ua
ua
(Ω )
(Ω )
ue
ue
ZWEITOR
R
ue(t)
4C
2C
2R
4R
C
ua
ϕ  u  (Ω )
a
 
 ue 
Bestimmen Sie die Eckfrequenzen, Grenzfrequenzen oder 3dB-Orte.
Für welche Frequenz(en) fi wird |ϕi| = π/4 ?
Für welche Frequenz wird |ϕ | maximal ?
____________________________________________________________________
______________________________________________________________________
Kurt Steudler
str
STR – ING
Elektrotechnik
10 - 6 - 10
_____________________________________________________________________
33.
Suchen Sie zu den unten gegebenen Amplitudengängen die zugehörige Schaltung
aus R-L und R-C Kombinationen, sowie die Phasengänge und Ortskurven.
a)
b)
lg Ω
d B |u a/u e|
lg Ω
d B |u a/u e|
20dB
p ro
20dB
p ro
c)
d)
lg Ω
d B |u a/u e|
lg Ω
d B |u a/u e|
20dB
p ro
20dB
p ro
e)
40dB
p ro
f)
lg Ω
d B |u a/u e|
lg Ω
d B |u a/u e|
40dB
p ro
80dB
p ro
60dB
p ro
g)
h)
lg Ω
d B |u a/u e|
lg Ω
d B |u a/u e|
20dB
p ro
40dB
p ro
60dB
p ro
______________________________________________________________________
Kurt Steudler
str
STR – ING
Elektrotechnik
10 - 6 - 11
_____________________________________________________________________
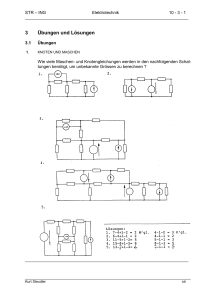
6.2
Lösungen
Z
1
Z 1 + jΩ
b)
Z = R + jωL
= 1 + jΩ
=
R
jωC
R
jΩ
R
Z
1
R ⋅ jωL Z
jΩ
Z=
d)
Z=
c)
=
=
1 + jωRC
R 1 + jΩ
R + jωL R 1 + jΩ
____________________________________________________________________
1.
a)
2.
Ω=
Z =R+
1
2
= 0,67593
f = 87,32 Hz
ϕ = - 0,976 rad ≙ - 55,94°
 ZPQ 

 −1
 R 
____________________________________________________________________
3.
a) |ZAB| = 1,1 kΩ b) ϕ1 = 1,151 rad ≙ 65,93° c) f = 26,86 kHz d) ϕ1 = 0,7854 rad
____________________________________________________________________
4.
aa) |ZXY|1 = 47,28 kΩ ab) |ZXY|0,1 = 21,67 kΩ ac) |ZXY|10 = 341,94 kΩ
ba) ϕ1 = - 0,3396 rad ≙ - 19,457° bb) ϕ0,1 = - 0,8138 rad ≙ - 46,63°
bc) ϕ1 = - 0,046 rad ≙ - 2,64°
____________________________________________________________________
5.
(
)
Z AB 1 − Ω 2 + j ⋅ 4Ω
=
R
− 2Ω ⋅ (Ω − j)
|ZAB|1 = 54,37 kΩ
ϕ1 = - 0,785 rad ≙ -45°
ϕ2 = 0,7374 rad ≙ - 42,25°
f2 = 4,85 kHz
____________________________________________________________________
6.
ZAB = 100 Ω - j 625 Ω
ZXY = (220 + j 48) Ω
____________________________________________________________________
7.
|Z| = 244,36 Ω
____________________________________________________________________
ua
L2
2
π
2û

=
=
⋅ sin ωt − 
ua ( t ) =
ue L1 + L 2 3
3
6

____________________________________________________________________
10.
ua
C1
1
π
û

=
=
ua ( t) = ⋅ sin ωt − 
ue C1 + C2 3
3
4

____________________________________________________________________
11.
______________________________________________________________________
Kurt Steudler
str
STR – ING
Elektrotechnik
10 - 6 - 12
_____________________________________________________________________
ua
R
1
=
=
ϕ = − arctan(Ω)
ΩEck = Ω0 = 1
ue R + jωL 1 + jΩ
____________________________________________________________________
12.
ua
R2
1
 kΩ 
=
=
ϕ = − arctan

1
ue R 2 + R1 + jωR1R 2C
 1+ k 
1+ + j ⋅ Ω
k
____________________________________________________________________
13.


k 2Ω

ϕ = arctan
 1 + k + k 2Ω 2 


____________________________________________________________________
14.
ua
R 2 + jωR1R 2C
1 + j ⋅ kΩ
=
=
ue R1 + R 2 + jωR1R 2C 1 + k + j ⋅ kΩ
ua
R2
1
 Ω 
=
=
ϕ = − arctan

ue R 2 + R1 + jωL 1 + k + j ⋅ Ω
 1+ k 
____________________________________________________________________
15.


Ω

ϕ = arctan
 k ⋅ (1 + k) + Ω 2 


____________________________________________________________________
16.
ua
R 2 + jωL
k + j⋅Ω
=
=
ue R 2 + R1 + jωL 1 + k + j ⋅ Ω
19.
SCHWINGKREIS
R
L
C
A
B
fo = 876,12 kHz
Der Serieschwingkreis liegt bei Resonanz auf
minimaler Impedanz und wirkt reell.
QSU = 983
B = 1,0173⋅10-3 B = 891,3 Hz
f2 = 876,57 kHz
f1 = 875,67 kHz
R = 560 mΩ, C = 330 pF, L = 100 µH
____________________________________________________________________
20.
SCHWINGKREIS
R
A
L
C
B
fo = 876,12 kHz
R = 12,111 Ω
B = 6,667⋅10-3
B = 5,841 kHz
f1 = 873,2 kHz
f2 = 879,05 kHz
QSU = 150, C = 100 pF, L = 330 µH
____________________________________________________________________
______________________________________________________________________
Kurt Steudler
str
STR – ING
Elektrotechnik
10 - 6 - 13
_____________________________________________________________________
21.


SCHWINGKREIS
R
1 + j ⋅ k ⋅ Ω −
L
A
z( Ω ) :=
C


1 − p ⋅ Ω ⋅ Ω −
B
C
1
Ω
1
1
+ j⋅ ⋅Ω
k
Ω
1 .10
5
1 .10
4
1 .10
3
R = 2 Ω, C = 820 pF, L = 200 µH
z( Ω )
100
10
1
0.1
1
1.5
2
Ω
____________________________________________________________________
22.
ZWEITOR
SCHWINGKREIS
Wirkt als Sperrfilter, Notchfilter.
Ri
ue
R
RKreis = 215,17 mΩ fo = 205,47 kHz
ua
RL
L
BN = 0,58426
C
BN = 120,05 kHz
AN = - 50,895 dB + 6,02 dB = 44,875 dB.
RL = Ri = 75 Ω, C = 12 nF, L = 50 µH, QSU = 300
____________________________________________________________________
23.
ZWEITOR
SCHWINGKREIS
Wirkt als Durchlassfilter, als Bandpass.
Ri
ue
R
L
C
RL
ua
fo = 205,47 kHz
B = 16,6 kHz
f1 = 197,34 kHz
QSL = 12,34
A = -0,366 dB an ?
RKreis = 2,1517 Ω.
f2 = 213,94 kHz
RL = Ri = 50 Ω, C = 1,2 nF, L = 500 µH, QSU = 300
____________________________________________________________________
______________________________________________________________________
Kurt Steudler
str
STR – ING
Elektrotechnik
10 - 6 - 14
_____________________________________________________________________
24.
SCHWINGKREIS
R
A
L
B
C
Bei Resonanz wirkt der Kreis hochohmig und
reell.
fo = 195,91 kHz
QPU = 91,18 (>>1, >10)
B = 2,15 kHz
B = 10,967⋅10-3
f2 = 196,99 kHz
f1 = 194,84 kHz
R = 2,7 Ω, C = 3,3 nF, L = 200 µH
____________________________________________________________________
(
) ( )
] ( )
ua
k p − Ω2 + j ⋅ p + k 2 ⋅ Ω
=
ue k p − (1 + p ) ⋅ Ω 2 + j ⋅ p + k 2 ⋅ Ω
____________________________________________________________________
25.
[
ua
j ⋅ 25Ω
=
ue 10 ⋅ 1 − Ω 2 + j ⋅ 39Ω
____________________________________________________________________
26.
(
)
ua
1 + j ⋅ (1 + p + q) ⋅ Ω
=
ue 1 + j ⋅ (1 + p )(1 + q) ⋅ Ω
____________________________________________________________________
25.
______________________________________________________________________
Kurt Steudler
str
STR – ING
Elektrotechnik
10 - 6 - 15
_____________________________________________________________________
33.
Suchen Sie zu den unten gegebenen Amplitudengängen die zugehörige Schaltung
aus R-L und R-C Kombinationen, sowie die Phasengänge und Ortskurven.
a)
b)
ϕ {u a/u e}
ϕ {u a/u e}
lg Ω
π /2
lg Ω
−π /2
d)
c)
ϕ {u a/u e}
π /2
ϕ {u a/u e}
π /2
lg Ω
lg Ω
−π
f)
e)
ϕ {u a/u e}
ϕ {u a/u e}
3 π /2
2π
lg Ω
lg Ω
−π
h)
g)
ϕ {u a/u e}
lg Ω
ϕ { u a/u e}
3 π /2
−π
π /2
lg Ω
______________________________________________________________________
Kurt Steudler
str
STR – ING
Elektrotechnik
10 - 6 - 16
_____________________________________________________________________
33.
Suchen Sie zu den unten gegebenen Amplitudengängen die zugehörige Schaltung
aus R-L und R-C Kombinationen, sowie die Phasengänge und Ortskurven.
a)
b)
c)
d)
e)
f)
3 M al
2 M al
4 M al
h)
g)
2 M al
4 M al
2 M al
______________________________________________________________________
Kurt Steudler
str