10 4 Ueb Elektrotechnik

STR – ING
Elektrotechnik
10 - 4 - 1
_____________________________________________________________________
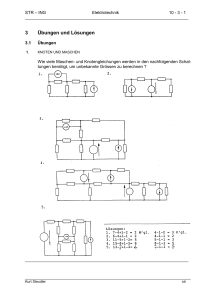
4 Übungen und Lösungen
4.1
1.
Übungen
Π - T – Transformation
x
y
x
3kΩ
2kΩ
y
2kΩ
2kΩ
z
2kΩ
3kΩ
z
z
z
Transformieren Sie das gegebene
Transformieren Sie das gegebene T –
Π - Netzwerk in ein T – Netzwerk.
Netzwerk in ein Π - Netzwerk.
____________________________________________________________________
2.
Π - und T – Netzwerk
Die dargestellte Black – Box, ein Zweitor, enthalte ein Π - Netzwerk oder ein T –
Netzwerk.
Blackbox
Rleer
Rkurz
Zweitor
Im Leerlauffall (Ausgangsklemmen ohne Last) messen wir am Zweitor (Black –
Box) einen Widerstand von R = 1,8 kΩ und im Kurschlussfall (Ausgangsklemmen
kurzgeschlossen) einen solchen von R = 800 Ω.
Bestimmen Sie die im Zweitor enthaltenen Elemente für ein Π - Netzwerk oder ein
T – Netzwerk. Die Netzwerke sind symmetrisch wie in Aufgabe 1.
____________________________________________________________________
3.
Lineare Operation
Eine mathematische Operation sei gegeben durch folgende Beziehung:
{
}
d f ( x ) ⋅ e y⋅ x
dx
Untersuchen Sie, ob Op{f(x)} eine lineare Operation ist.
____________________________________________________________________
F(y) = Op{f ( x )} =
4.
R1
U1
R2
Gegeben sind:
R1 = 330 Ω R2 = 560 Ω R3 = 270 Ω
R4 = 680 Ω U1 = 6 V
R3
R4
U2
Ux
Um wie viel ändert sich die Spannung Ux,
wenn U2 von + 1 V auf – 1 V geändert
wird ?
____________________________________________________________________
______________________________________________________________________
Kurt Steudler
str
STR – ING
Elektrotechnik
10 - 4 - 2
_____________________________________________________________________
5.
R1
Gegeben sind:
R2 = 3 kΩ
R1 = 6 kΩ
R4 = 1 kΩ
R5 = 2 kΩ
R2
U
Ux
R5
R3
R4
R3 = 2 kΩ
U = 10 V
Um wie viel ändert sich der Strom I5, wenn
die Spannung Ux von 0 V auf 300 mV ansteigt ?
____________________________________________________________________
6.
Theorem von Thévenin
I
R1
U
A
R2
R3
R4
B
R1 = 390 Ω R2 = 560 Ω R3 = 680 Ω
R4 = 1,5 kΩ I = 1,2 mA U = 30 V
Bestimmen Sie das Ersatzschaltbild
A
UTh Rr
B
a)
formal und
b)
mit den gegebenen Werten.
____________________________________________________________________
7.
Theorem von Norton
I
R1
U
A
R2
R3
R4
B
R1 = 3,9 kΩ R2 = 680 Ω R3 = 820 Ω
R4 = 1,5 kΩ I = 1,8 mA U = 24 V
Bestimmen Sie das Ersatzschaltbild
A
Rr
IN
B
a)
formal und
b)
mit den gegebenen Werten.
____________________________________________________________________
R1 = 8,2 kΩ R2 = 1,8 kΩ R3 = 680 Ω
R
U = 12 V
4 = 1,5 kΩ I = 1,2 mA
A
U
Bestimmen Sie das Ersatzschaltbild
I
A
R2
Rr
R3
UTh
B
R1 R3
R4
B
a)
formal und
b)
mit den gegebenen Werten.
____________________________________________________________________
8.
Theorem von Thévenin
______________________________________________________________________
Kurt Steudler
str
STR – ING
Elektrotechnik
10 - 4 - 3
_____________________________________________________________________
R1 = 4,7 kΩ R2 = 820 Ω R3 = 470 Ω
R4 = 2,7 kΩ I = 2 mA
U = 15 V
A
U
Bestimmen Sie das Ersatzschaltbild
I
A
R2
Rr
R3
IN
B
R1 R3
R4
B
a)
formal und
b)
mit den gegebenen Werten.
____________________________________________________________________
9.
10.
Theorem von Norton
Bestimmen Sie für die beiden folgenden Schaltungen die Ersatzschaltbilder nach
Thévenin und Norton.
R1
R2
R4
R3
U
A
I
R6
R5
B
R8
R7
A
B
____________________________________________________________________
11.
Leiteranalyse
Bestimmen Sie UX , UY und IZ .
5,6 kΩ
2,7 kΩ
1,8 kΩ
20 mA
UY
68 kΩ
2,2 kΩ
33 kΩ
100 Ω
4,7 kΩ
560 Ω
820 kΩ
UX
IZ
____________________________________________________________________
12.
Anpassung
DATENSENDER
ROUT = 60 Ω
analoge Daten
PEGELMESSGERÄT
Π
od T
ANP 1
Leitung
50 Ω
Π
od T
RIN = 75 Ω
ANP 2
Dimensionieren Sie die Blöcke ANP 1 (mit einem T – Glied) und ANP 2 (mit einem
Π - Glied) so, dass die Dämpfung zwischen Datensender und Pegelmesser A = 40 dB beträgt.
Die beiden Blöcke ANP 1 und ANP 2 stellen je Anpassung her.
____________________________________________________________________
______________________________________________________________________
Kurt Steudler
str
STR – ING
Elektrotechnik
10 - 4 - 4
_____________________________________________________________________
13.
Stellen Sie die nachfolgenden Funktion Modulo T mathematisch dar.
u(t)
V
10
t
0
5
s
T
______________________________________________________________________
14.
Stellen Sie die nachfolgenden Funktion Modulo T mathematisch dar.
i(t)
I
t
0
T
______________________________________________________________________
______________________________________________________________________
Kurt Steudler
str
STR – ING
Elektrotechnik
10 - 4 - 5
_____________________________________________________________________
15.
Stellen Sie die nachfolgenden Funktion Modulo T mathematisch dar.
u(t)
V
10
t
0
5
s
T
______________________________________________________________________
16.
Stellen Sie die nachfolgenden Funktion Modulo T mathematisch dar.
u(t)
U
sinusförmig
t
0
T
______________________________________________________________________
______________________________________________________________________
Kurt Steudler
str
STR – ING
Elektrotechnik
10 - 4 - 6
_____________________________________________________________________
4.2
6.
Lösungen
THEOREM VON THÉVENIN
Rr = R4||(R2 + R1||R3)=
Gesucht sind UTh und Rr
R 4 ⋅ (R1R 2 + R 2 R 3 + R 3 R1)
= 525,067 Ω
R 4 ⋅ (R1 + R 3) + (R1R 2 + R 2 R 3 + R 3 R1)
R 3 || (R 2 + R 4) ⋅ R 4 - ⋅
R2 ⋅ R4
=
Iy
R1 + R 3 || (R 2 + R 4) R 2 + R 4
R 2 + R1 || R 3 + R 4
R 4 ⋅ [Ux ⋅ R 3 - Iy ⋅ R 2 (R1 + R 3)]
= 11,955 V
=
R 4 ⋅ (R1 + R 3) + (R1R 2 + R 2 R 3 + R 3 R1)
______________________________________________________________________
UTh= Ux ⋅
7.
THEOREM VON NORTON
Rr = R4||(R2 + R1||R3)=
Gesucht sind IN und Rr
R 4 ⋅ (R1R 2 + R 2 R 3 + R 3 R1)
= 712,61 Ω
R 4 ⋅ (R1 + R 3) + (R1R 2 + R 2 R 3 + R 3 R1)
(Ux ⋅ R 3 - Iy ⋅ R 2) ⋅ (R1 + R 3)
= 2,17 mA
R1R 2 + R 2 R 3 + R 3 R1
______________________________________________________________________
IN =
8.
THEOREM VON THÉVENIN
Gesucht sind UTh und Rr
⋅( + )
Rr = R4||(R1 + R2) = R 4 R1 R 2 = 1,304 kΩ
R1 + R 2 + R 4
Ux ⋅ (R1 + R 2) + Iy ⋅ R1R 4
Iy R1 - Ux
⋅ R 4 + Ux =
= 11,718 V
R1 + R 2 + R 4
R1 + R 2 + R 4
______________________________________________________________________
UTh=
9.
THEOREM VON NORTON
Gesucht sind IN und Rr
⋅( + )
Rr = R4||(R1 + R2) = R 4 R1 R 2 = 1,179 kΩ
R1 + R 2 + R 4
Ux ⋅ (R1 + R 2) + Iy ⋅ R1R 4
Iy ⋅ R 1 U x
+
=
= 7,258 mA
(R1 + R 2) ⋅ R 4
R1 + R 2 R 4
______________________________________________________________________
IN=
______________________________________________________________________
Kurt Steudler
str
STR – ING
Elektrotechnik
10 - 4 - 7
_____________________________________________________________________
10.
THEOREME
Ersatzschaltbilder
( + )( + ) +
R3
Fall a) Rr = R4 + R3||(R1 + R2) = R1 R 2 R3 R 4 R3 R 4 UTh = U ⋅
R1 + R 2 + R3
R1 + R 2 + R 3
U ⋅ R3
U
⋅ R3
=
IN =
(R1 + R 2)(R 3 + R 4) + R 3 R 4
R1 + R 2 + R 3 || R 4 R 3 + R 4
( + )( + ) +
R7
Fall b) Rr = R8 + R7||(R5 + R6) = R5 R6 R7 R8 R7 R8 UTh = I ⋅ R 5 ⋅
R5 + R 6 + R 7
R5 + R 6 + R7
I ⋅ R5
I ⋅ R5 ⋅ R 7 R8
=
IN =
(R 5 + R 6)(R 7 + R 8) + R 7 R 8
R 5 + R 6 + R 7 || R 8
______________________________________________________________________
13.
 10 V ; 1s ≤ t ≤ 3 s 
− 4 V ; 3 s ≤ t ≤ 6 s 


u( t) = 
 Modulo T = 7 s
 6 V ; 6 s ≤ t ≤ 7 s
− 8 V ; 7 s ≤ t ≤ 8 s 
______________________________________________________________________
14.
T
T
5⋅T

3 ⋅ I
;
≤t≤

 T ⋅ (t − 12 )
12
12


5⋅T
11⋅ T 
− 3 ⋅ I ⋅ (t − 3 ⋅ T )
;
≤t≤
 T
4
12
12 
u( t) = 
 Modulo T
11⋅ T

 6 ⋅ I ⋅ ( t − 11⋅ T )
;
≤t≤T

 T
12
12
 6 ⋅I
13 ⋅ T
13 ⋅ T 

−
) ; T≤t≤
⋅ (t −
12
12

 T
______________________________________________________________________
15.
5 Vs −1 ⋅ (t − 0,5 s )
; 0,5 s ≤ t ≤ 2,5 s 


− 5,3 Vs −1 ⋅ (t − 2,5 s ) + 10 V ; 2,5 s ≤ t ≤ 5,5 s 
u( t) = 
 Modulo T = 6 s
−1
; 5,5 s ≤ t ≤ 6 s 
28 Vs ⋅ (t − 5,5 s ) − 6 V


− 16 Vs −1 ⋅ (t − 6,5 s )
; 6 s ≤ t ≤ 6,5 s 
______________________________________________________________________
______________________________________________________________________
Kurt Steudler
str
STR – ING
Elektrotechnik
10 - 4 - 8
_____________________________________________________________________
16.
 2 ⋅U  T 
T
5⋅T 
≤t≤
;
 T ⋅t − 6 
6
12 




 4 ⋅U
3⋅π 5⋅T
7⋅T 
3⋅π
⋅ sin
⋅t−
≤t≤
;


4 
12
12 
 T
 3
u( t) = 
 Modulo T
⋅
⋅
π
⋅
π
⋅
⋅
4
U
3
7
7
T
11
T




⋅ sin
⋅t −
≤t≤
;
 3
4 
12
12 
 T


11⋅ T
14 ⋅ T 
− 2 ⋅ U ⋅  t − 11⋅ T 
≤t≤
;

 T 
12 
12
12 
______________________________________________________________________
______________________________________________________________________
Kurt Steudler
str