Übungsaufgabe Monopolfall quadratische Funktionen

Anwendungsaufgabe: Quadratische Funktionen: Monopolfall
Die Nachfragefunktion eines Angebotsmonopolisten lautet: p(x) = 10 – x. Die
Kapazitätsgrenze des Monopolisten liegt bei 11 Mengeneinheiten.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
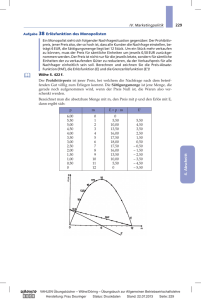
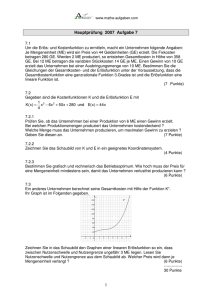
Zeichnen Sie die Nachfragefunktion in den ersten Quadranten eines p-xKoordinatensystems. p-Achse bis 25, x-Achse bis 11 Einheiten.
Berechnen Sie die Erlösfunktion des Monopolisten, indem Sie die Beziehung
E(x) = p(x) * x anwenden!
Berechnen Sie die erlösmaximale Menge und den maximalen Erlös, indem Sie
den Scheitelpunkt der Erlösfunktion bestimmen!
Berechnen Sie die Nullstellen der Erlösfunktion! Begründen Sie ökonomisch,
warum die Erlösfunktion an den ermittelten Stellen null sein muss!
Zeichen Sie die Erlösfunktion in das Koordinatensystem ein!
Bestimmen Sie den ökonomisch sinnvollen Definitionsbereich D(E) = {? ≤ x ≤ ?}
der Erlösfunktion!
Bestimmen Sie den ökonomisch sinnvollen Wertebereich W(E) = {? ≤ E ≤ ?} der
Erlösfunktion!
Die Kostenfunktion des Monopolisten ist gegeben durch K(x) = 12 + 2x.
Berechnen Sie die Schnittpunkte der Kostenfunktion mit der Erlösfunktion!
Überprüfen Sie Ihre Ergebniswerte zu der unter Aufgabe 8 gelösten
quadratischen Gleichung mit dem Satz von Vieta!
Zeichnen Sie die Kostenfunktion in das Koordinatensystem ein!
Interpretieren Sie die Schnittpunkte von Kosten- und Erlösfunktion ökonomisch!
Berechnen Sie die Gewinnfunktion G(x) = E(x) – K(x)!
Berechnen Sie die gewinnmaximale Menge und den maximalen Gewinn in GE,
indem Sie den Scheitelpunkt der Gewinnfunktion bestimmen!
Berechnen Sie die Nullstellen der Gewinnfunktion (Gewinnschwelle und
Gewinngrenze), und bestimmen Sie das zugehörige Gewinnintervall xG  [ / ]!
Zeichnen Sie die Gewinnfunktion in das Koordinatensystem ein!
Bestimmen Sie graphisch und rechnerisch den Cournotschen Punkt, indem Sie
der gewinnmaximalen Ausbringungsmenge den Preis zuweisen, den der
Monopolist fordern muss, um seinen Gewinn zu maximieren!
Bestimmen Sie den gewinnmaximalen Erlös!
Bestimmen Sie den Definitionsbereich D(G) = {? ≤ x ≤ ?} der Gewinnfunktion!
Bestimmen Sie den Wertebereich W(E) = {? ≤ E ≤ ?} der Gewinnfunktion!
Stellen Sie die Gewinnfunktion in Linearfaktorzerlegung dar!
1
Lösungsvorlage
K(x), E(x), G(x), p(x)












x










2
Lösungen:
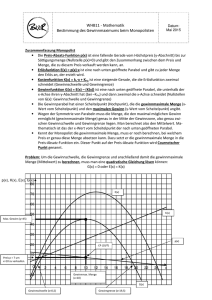
y(x)
24
22
20
18
16
14
12
10
8
6
4
2
x
1
2
3
4
5
6
7
8
9
10
3
zu 2) Erlösfunktion
E(x) = p(x) * x = (10 – x) * x = 10x – x2
zu 3) Scheitelpunkt der Erlösfunktion
E(x)
= -x2 + 10x
E(x)
= -1 * [x2 – 10x]
= -1 * [x2 – 10x + 52 – 52]
= -1 * [(x – 5)2 – 25]
= -1 * (x – 5)2 + 25
Scheitelpunkt S(5/25)
erlösmaximale Menge: 5 ME
maximaler Erlöse: 25 GE
zu 4) Nullstellen der Erlösfunktion
E(x) = 0
-x2 + 10x = 0
x * (-x + 10) = 0
│:x
x01 = 0
-x + 10 = 0
x02 = 10
zu 6) Definitionsbereich D(E) = {0 ≤ x ≤ 11} der Erlösfunktion!
zu 7) Wertebereich W(E) = {0 ≤ E ≤ 25} der Erlösfunktion!
zu 8) Schnittpunkte von Kosten- und Erlösfunktion
E(x) = K(x)
-x2 + 10x = 12 + 2x
│-12 – 2x
-x2 + 8x – 12 = 0
│* (-1)
4
x2 – 8x + 12 = 0
x2 – 8x + 42 – 42 + 12 = 0
(x – 4)2 – 16 + 12 = 0
(x – 4)2 – 4 = 0
(x – 4)2 = 4
│√
x–4=2
x1 = 6
x – 4 = -2
x2 = 2
Mit er p-q-Formel:
-x2 + 8x – 12 = 0
│* (-1)
x2 – 8x + 12 = 0
p= -8 und q=-12
2
p
x1/2 = - 
2
 p
 
2
2
q
=
4 
8
 
2
 12
=4  2
x1 = 6 und x2 = 2
zu 9) Satz von Vieta zur Prüfung des Ergebnisses aus Aufgabe 8
x1 + x2 = -p
6+ 2 = 8 = -p
Wenn in Aufgabe 8 galt, p = -8, folgt –p = -(-8) = 8
q.e.d.
zu 11)
Wo die Kostenfunktion die Erlösfunktion schneidet, ist der Gewinn gleich 0.
zu 12) Gewinnfunktion berechnen
G(x) = E(x) – K(x)
= 10x – x2 – (12 + 20)
5
= 10x – x2 – 12 – 2x
= -x2 + 8x – 12
zu 13) Scheitelpunkt der Gewinnfunktion
G(x)
= -x2 + 8x – 12
= -1 * [x2 – 8x + 12]
= -1 * [x2 – 8x + 42 - 42 + 12]
= -1 * [(x -4)2 – 16 + 12]
= -1 * [(x – 4)2 – 4]
= -1 * (x – 4)2 + 4
S(4 / 4)
gewinnmaximale Menge: 4 ME
maximaler Gewinn: 4 GE
zu 14) Nullstellen der Gewinnfunkion
G(x) = 0
-x2 + 8x – 12 = 0
│*(-1)
x2 - 8x + 12 = 0
Ergebnis siehe oben unter Aufgabe 8:
x1 = 6 und x2 = 2
zu 16) Cournotscher Punkt
p(x) = 10 – x
p(xG = 4) = 10 – 4 = 6
CP(4 / 6)
Der Monopolist muss 6 GE/ME verlangen, um seinen Gewinn zu maximieren.
6
zu 17) Gewinnmaximaler Umsatz
E(xG) = 10x – x2
E(xG = 4) = 10* 4 – 16
E(4) = 24 GE
zu 18) Definitionsbereich D(G) = {0 ≤ x ≤ 11} der Gewinnfunktion!
zu 19) Bestimmen Sie den Wertebereich W(E) = {0 ≤ G ≤ 4} der Gewinnfunktion!
zu 20 ) Gewinnfunktion in Linearfaktorzerlegung
G(x)
= -x2 + 8x – 12
= -1 * [x2 – 8x + 12]
Nullstellen bei x1 = 6 und x2 = 2, vgl. Aufgabe 14 als Ergebnis von x2 – 8x + 12 = 0.
G(x) = -1 * [(x-6) * (x-2)]
Probe: G(x) = -1 * [x2 – 6x – 2x + 12] = -1 * [x2 – 8x + 12] = -x2 + 8x -12
7