Brechung File
Werbung
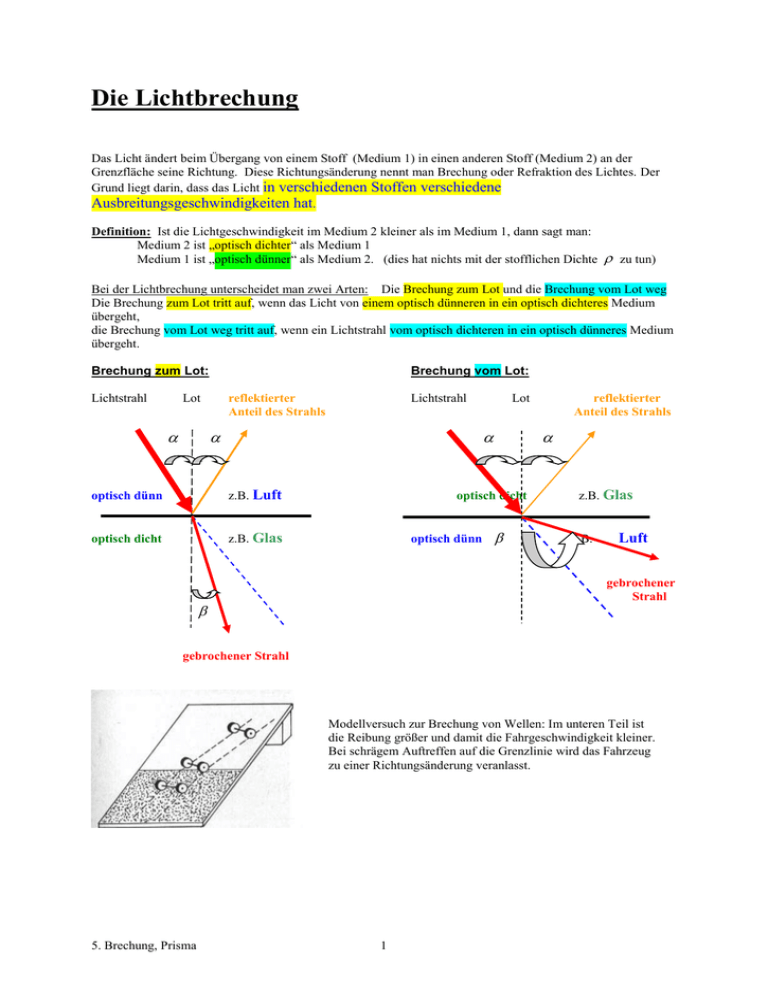
Die Lichtbrechung Das Licht ändert beim Übergang von einem Stoff (Medium 1) in einen anderen Stoff (Medium 2) an der Grenzfläche seine Richtung. Diese Richtungsänderung nennt man Brechung oder Refraktion des Lichtes. Der Grund liegt darin, dass das Licht in verschiedenen Stoffen verschiedene Ausbreitungsgeschwindigkeiten hat. Definition: Ist die Lichtgeschwindigkeit im Medium 2 kleiner als im Medium 1, dann sagt man: Medium 2 ist „optisch dichter“ als Medium 1 Medium 1 ist „optisch dünner“ als Medium 2. (dies hat nichts mit der stofflichen Dichte zu tun) Bei der Lichtbrechung unterscheidet man zwei Arten: Die Brechung zum Lot und die Brechung vom Lot weg Die Brechung zum Lot tritt auf, wenn das Licht von einem optisch dünneren in ein optisch dichteres Medium übergeht, die Brechung vom Lot weg tritt auf, wenn ein Lichtstrahl vom optisch dichteren in ein optisch dünneres Medium übergeht. Brechung zum Lot: Lichtstrahl Brechung vom Lot: Lot reflektierter Anteil des Strahls Lichtstrahl Lot optisch dünn z.B. Luft optisch dicht z.B. Glas optisch dicht optisch dünn reflektierter Anteil des Strahls z.B. Glas z.B. Luft gebrochener Strahl gebrochener Strahl Modellversuch zur Brechung von Wellen: Im unteren Teil ist die Reibung größer und damit die Fahrgeschwindigkeit kleiner. Bei schrägem Auftreffen auf die Grenzlinie wird das Fahrzeug zu einer Richtungsänderung veranlasst. 5. Brechung, Prisma 1 Das Brechungsgesetz von Snellius: Ptolemaios (150 n.Ch) maß für verschiedene Einfallswinkel den zugehörigen Brechungswinkel und fasste die Wertepaare in Tabellen zusammen. Er stellte fest, dass für jedes durchsichtige Medium eine eigene Tabelle angefertigt werden muss, war aber nicht in der Lage, aus den Tabellen das zugrunde liegende Gesetz abzulesen. Dies gelang erst 1500 Jahre später dem holländischen Mathematiker Willebrord Snellius. Er erkannte, dass nicht die Winkelwerte von Einfalls- und Brechungswinkel in einem bestimmten Verhältnis stehen, sondern die Sinuswerte dieser Winkel. Für jeden Stoff hat das Verhältnis sin einen festen Wert. sin Beim Übergang von Luft in Wasser beträgt er 1,33. Beim Übergang von Luft in Glas hat es den Wert 1,50. Man nennt dieses Verhältnis Brechzahl oder Brechungsindex und bezeichnet es mit n. Die Brechzahl n ist eine dimensionslose physikalische Größe. Substanz bei 20 °C Luft: bei einem Druck von 1013 hPa reines Wasser Benzol Diamant Streusalz Flintglas Brechungsindex n 1,00027 1,333 1,501 2,417 1,544 1,613 Brechungsgesetz: Der einfallende Strahl, das Lot auf die Körperoberfläche und der gebrochene Strahl liegen stets in einer Ebene. Beim Übertritt vom Vakuum in ein Medium gilt für alle Einfallswinkel: c sin n = vakuum sin c medium n hat für jedes Medium (auf Vakuum bezogen) einen eigenen Wert. Tritt Licht nicht vom Vakuum aus sondern von einem Medium 1 in ein Medium 2, dann gilt n sin 2 sin n1 c1 c2 für n2 schreibt man auch n12 relativer Brechungsindex n1 n1 und n2 heißen dann absoluter Brechungsindex 5. Brechung, Prisma 2 Auf Grund der Lichtbrechung kommt es zu optischen Täuschungen, da das Auge immer die ins Auge fallenden Strahlen geradlinig nach hinten verlängert. Man „sieht“ daher einen Gegenstand oft an einer anderen Stelle, als er sich tatsächlich befindet. Das rechte Bild ist eine Fotomontage: links: Die Tasse ist leer. Am Boden liegt eine Münze, die aber nicht sichtbar ist, weil sie sich unter dem Tassenrand befindet. rechts: Die Tasse ist mit Wasser gefüllt. Die am Boden liegende Münze ist sichtbar geworden. Das Fermatsche Prinzip: Nach der Entdeckung des Brechungsgesetzes durch Snellius rätselten viele Naturphilosophen, weshalb das Licht gerade so verläuft, dass es dem Brechungsgesetz genügt. Eine überraschende Antwort fand der Mathematiker Pierre de Fermat. Er wendete die Differentialrechnung auf das Problem der Lichtausbreitung an und entdeckte: Licht läuft immer so vom Punkt A zum Punkt B, dass es die kürzeste Zeit benötigt. Totalreflexion: Bei der Brechung vom Lot tritt ab einem bestimmten Einfallswinkel ein Grenzfall auf. Der Brechungswinkel wird 90°. Das heißt, der Lichtstrahl gleitet entlang der Grenzfläche zwischen den Medien. Wird der Einfallswinkel weiter erhöht, dann gibt es keinen gebrochenen Strahl mehr. Das gesamte Licht wird vollständig reflektiert. Diese Reflexion nennt man Totalreflexion. Gleiten des Lichtstrahls entlang der Grenzfläche Totalreflexion (Reflexionsgesetz) Glas oder Wasser Grenzwinkel Glas oder Wasser Grenzwinkel G 90° optisch dünneres Medium (Luft oder Vakuum) 5. Brechung, Prisma optisch dünneres Medium (Luft oder Vakuum) 3 Anwendungen: Lichtleiter (Fiberoptik) Jeder einfallende Lichtstrahl wird an den Begrenzungsflächen stets total reflektiert und verbleibt somit innerhalb des Leiters. Digitale Signale in Form von Lichtimpulsen lassen sich auf diese Weise parallel in tausenden von feinen Glasfaserkabeln übertragen. Endoskopie: 5. Brechung, Prisma 4 (1) Dies ist der Schlauch, der in den Magen eingeführt wird. Er enthält Optik und Arbeitskanäle (Spülen, Gewebeentnahme etc.). Er ist sehr flexibel und nur 9.8mm dünn (2) Über diese Kupplung wird das Licht in die Fiberglasoptik des Gastroskops gebracht. Zusätzlich können Luft und Wasser in den Gastroskopschlauch eingeleitet werden. Magenwand mit Geschwür (3) Der Handgriff enthält die Kupplung für die Videooptik bzw. die Linse zum "Hindurchschauen" Über verschiedene Räder werden die Funktionen gesteuert (z.B. Spülen) und das vordere Ende des Schlauchs bewegt. (4) Mit diesem Handgriff wird die Entnahme von Gewebe durchgeführt. Der Gastroskopschlauch ist sehr flexibel und kann vom Arzt in die verschiedenen Richtungen dirigiert werden. Damit ist es möglich, die unterschiedlichen Regionen von Magen und Zwölffingerdarm anzusehen Luftspiegelung (Fata Morgana) Wird die Bodenfläche durch die Sonne stark erwärmt, so bildet sich unmittelbar über dem Boden eine heiße Luftschicht. Trotz der Luftzirkulation (heiße Luft steigt nach oben, kühle Luft sinkt nach unten) ist im Sommer die an den Boden angrenzende Luftschicht wärmer als die darüber liegende. Lichtstrahlen, die schräg auf diese heiße Luftschicht auftreffen, werden totalreflektiert. Die heiße Luftschicht wirkt als Spiegel und kann Wasserflächen vortäuschen. Es können sich auch in großen Höhen warme Luftschichten mit geringer Dichte bilden. An dieser Schicht werden dann schräg nach oben gehende Lichtstrahlen nach unten reflektiert. So kann man das Spiegelbild einer Landschaft am Himmel sehen. 5. Brechung, Prisma 5 Die atmosphärische Strahlenbrechung Sterne scheinen, wenn sie nahe am Horizont sind, höher zu stehen. Ursache hierfür ist die mehrmalige Brechung des Lichts an den unterschiedlich dichten Schichten der Lufthülle. Am Horizont beträgt die scheinbare Anhebung der Sterne 0,5°. 3.3.1. Die planparallele Platte: Durch die zweimalige Brechung, einmal zum Lot und einmal vom Lot, kommt es zu einer Parallelverschiebung des Lichtstrahls. Je dicker die Platte ist, desto größer wird die Parallelverschiebung. Leite die Formel für die Parallelverschiebung selbst her: Zeige, dass mit Verwendung des Brechungsgesetzes sich s = f(d, , n) s wird Null für d=0 oder =0 oder n=1 Lichtbrechung bei optischen Prismen: 5. Brechung, Prisma 6 s d. sin( ) cos cos s d . sin .1 2 n sin 2 ergibt. Im rechten Bild ist der brechende Winkel Fällt ein Lichtstrahl senkrecht zur brechenden Kante auf ein Prisma, so wird er im Allgemeinen zweimal gebrochen. Der Strahl erfährt daher eine starke Ablenkung, die von der brechenden Kante weggerichtet ist. Der Ablenkwinkel ist umso größer, je größer der brechende Winkel des Prismas ist. brechende Kante Der Ablenkwinkel hängt auch vom Einfallswinkel 1 ab. Die kleinste Strahlablenkung stellt sich ein, wenn der Strahlengang symmetrisch ist also 1 = 2 gilt. Basis Wenn der Winkel größer. Der Ablenkwinkel ist daher auch größer. 2 größer als der Grenzwinkel G wird, kommt es an der zweiten Prismenfläche zur Totalreflexion: ε φ φ ........... Winkel der Gesamtablenkung α β 180 – ε α’ Weil der Grenzwinkel beim Übergang von Glas in Luft ca. 42° beträgt, kann man mit einem Glasprisma, dessen Winkel 90°, 45° und 45° betragen, Parallelstrahlenbündel durch Totalreflexion um 90° oder 180° ablenken. Man kann auch die Reihenfolge der Strahlen vertauschen. 5. Brechung, Prisma 7 Übungsbeispiele zur Brechung 1) Auf ein gleichseitiges Prisma aus leichtem Kronglas fällt Licht. (n = 1,51) Berechnen Sie die beiden Brechungswinkel, zeichnen Sie den Strahlenverlauf des Lichtes! Entscheiden Sie, ob beim Variieren des Einfallswinkels eine Totalreflexion an der Grenzfläche Glas-Luft erfolgen kann! Begründen Sie Ihre Entscheidung. 2) Unter welchen Bedingungen tritt Totalreflexion des Lichtes auf? Berechnen Sie den Grenzwinkel der Totalreflexion an der Grenzfläche schweres Flintglas - Luft! Auf zwei Prismen aus schwerem Flintglas fällt Licht. Entscheiden Sie für jedes der beiden Prismen, ob das Licht an der Grenzfläche Glas - Luft gebrochen oder total reflektiert wird! Begründen Sie Ihre Entscheidung! Zeichnen Sie den Strahlenverlauf durch jedes der beiden Prismen! 3) Zwei gleichschenklige, rechtwinklige Prismen aus Flintglas (nF=1,75) und Kronglas (nK = 1,51) sind zusammengesetzt. Unter welchem Winkel verlässt das einfarbige Lichtbündel den Glaskörper. 10) Ein Fischer schaut vom Boot, aus 360 cm Höhe normal auf die Wasseroberfläche. 240 cm unter der Wasseroberfläche befindet sich in Blickrichtung ein Fisch (n wasser = 4 ). 3 a) Wie groß ist die scheinbare Entfernung des Fischs von seinem Auge? Wie groß ist die scheinbare Annäherung? b) Wie groß ist für den Fisch die scheinbare Entfernung des Fischers? Wie groß ist der Unterschied zwischen scheinbarer und tatsächlicher Entfernung? 11) Der Brechungsindex von Wasser beträgt 1,33, der von einem Stück Kronglas 1,54. Berechne den Brechungsindex von Glas, wenn es sich im Wasser befindet. Wie groß ist der Grenzwinkel zwischen Glas und Wasser? 12) Unter welchem Winkel muss ein Lichtstrahl vom Vakuum auf Glas (nG) fallen, wenn der reflektiert Strahl und der gebrochene Strahl aufeinander normal stehen sollen? 15) Ein gerader Stab, der teilweise im Wasser steht (n=4/3), scheint einen Winkel von 45° mit der Oberfläche zu bilden, wenn man senkrecht hineinsieht. Wie groß ist die tatsächliche Neigung des Stabes? 16) Ein Prisma, mit dem brechenden Winkel =46°, verursacht eine minimale Ablenkung von 32°. Berechne den Brechungsindex des Prismas. 22) Wie kann man die Erscheinung der Fata Morgana erklären? 23) Wo ist die Reflexion besser (d.h.: Wo wird mehr der einfallenden Lichtenergie reflektiert): An einem guten Metallspiegel oder bei Totalreflexion? 24) Warum erscheint die Sonne beim Untergang a) rot und b) flachgedrückt? 5. Brechung, Prisma 8 Lösungen: 1) 1. Berechnung des Brechungswinkels : Mit Hilfe dieses Winkels muss nun der Einfallswinkel auf der gegenüberliegenden Seite bestimmt werden. Mit diesem Einfallswinkel wird nun der Brechungswinkel berechnet. Da es ein Übergang von optisch dicht zu optisch dünn ist, muss der Kehrwert der Brechzahl verwendet werden. Um zu prüfen, ob Totalreflexion möglich ist, muss der zweite Brechungswinkel 90° gesetzt werden und zurück gerechnet werden. Damit erhält man dann einen Einfallswinkel von 28,7°. Bei allen Einfallswinkeln, die kleiner als dieser Winkel sind, tritt Totalreflexion auf, das heißt, der Lichtstrahl verlässt an dieser Seite das Prisma nicht. Antwort: Der Austrittswinkel beträgt 79,9°. Bei kleineren Einfallswinkeln als 28,7° tritt Totalreflexion auf. 2) (Der Einfallswinkel ist immer der Winkel zwischen dem Strahl und dem Einfallslot. Das Lot steht senkrecht auf der Grenzfläche) Da der Einfallswinkel im ersten Fall kleiner als 34,85° ist, wird ganz normal gebrochen. Der Brechungswinkel berechnet sich: Beim zweiten Prisma ist der Einfallswinkel 45°, also größer als der Grenzwinkel. Damit wird der Strahl an der Grenzfläche Glas - Luft reflektiert und trifft im rechten Winkel auf die untere Grenzfläche, durch die er ohne weitere Ablenkung hindurchgeht. 5. Brechung, Prisma 9 3) Lösung: Am Übergang Luft - Flintglas erfolgt keine Brechung, da der Strahl senkrecht einfällt. Die Brechzahl für den Übergang Flintglas Kronglas ist nF/nK Für den Einfallswinkel 2 muss zuerst der Winkel berechnet werden. Damit berechnet man nun den zweiten Brechungswinkel: Es ist der Austrittswinkel gesucht. Antwort: Das Licht tritt unter einem Winkel von 74,8° aus dem Glas aus. 10) a) 540 cm ; Annäherung 60 cm b) 720 cm ; 120 cm weiter weg 11) nwg = 1,16 Grenzwinkel = 59,6° 12) arctan n 15) 53° 16) n=1,61 22) Heiße Luft hat einen etwas kleineren Brechungsindex als kalte. Totalreflexion des Lichtes an heißen Luftschichten. 23) Bei Totalreflexion 24) a) langwelliges (rotes) Licht durchdringt Dunst (Atmosphäre) besser als kurzwelliges (blaues); b) durch die Brechung der Strahlen beim Durchgang durch die Atmosphäre) 5. Brechung, Prisma 10