Aufgabe zum Thema Richtungswinkel und Entfernung

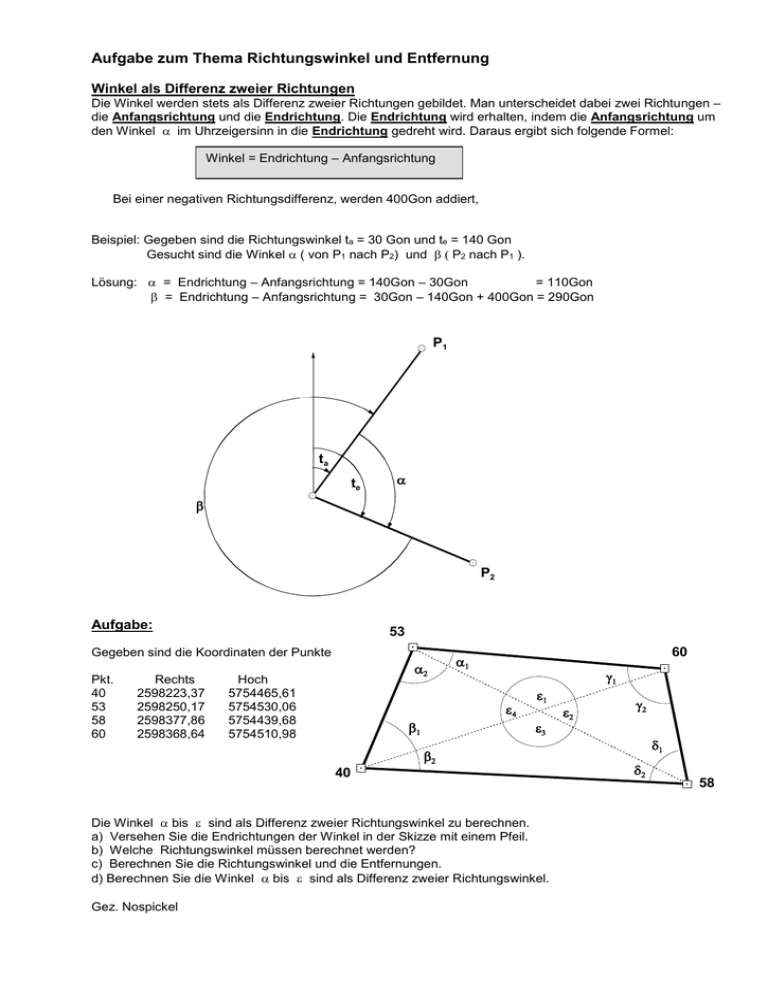
Aufgabe zum Thema Richtungswinkel und Entfernung
Winkel als Differenz zweier Richtungen
Die Winkel werden stets als Differenz zweier Richtungen gebildet. Man unterscheidet dabei zwei Richtungen –
die Anfangsrichtung und die Endrichtung. Die Endrichtung wird erhalten, indem die Anfangsrichtung um
den Winkel  im Uhrzeigersinn in die Endrichtung gedreht wird. Daraus ergibt sich folgende Formel:
Winkel = Endrichtung – Anfangsrichtung
Bei einer negativen Richtungsdifferenz, werden 400Gon addiert,
Beispiel: Gegeben sind die Richtungswinkel ta = 30 Gon und te = 140 Gon
Gesucht sind die Winkel  ( von P1 nach P2) und P2 nach P1 ).
Lösung:  = Endrichtung – Anfangsrichtung = 140Gon – 30Gon
= 110Gon
 = Endrichtung – Anfangsrichtung = 30Gon – 140Gon + 400Gon = 290Gon
P1
ta
te


P2
Aufgabe:
53
Gegeben sind die Koordinaten der Punkte
Pkt.
40
53
58
60
Rechts
2598223,37
2598250,17
2598377,86
2598368,64

Hoch
5754465,61
5754530,06
5754439,68
5754510,98
60







40
Die Winkel  bis  sind als Differenz zweier Richtungswinkel zu berechnen.
a) Versehen Sie die Endrichtungen der Winkel in der Skizze mit einem Pfeil.
b) Welche Richtungswinkel müssen berechnet werden?
c) Berechnen Sie die Richtungswinkel und die Entfernungen.
d) Berechnen Sie die Winkel  bis  sind als Differenz zweier Richtungswinkel.
Gez. Nospickel




58