5 Arbeitsblätter
Werbung
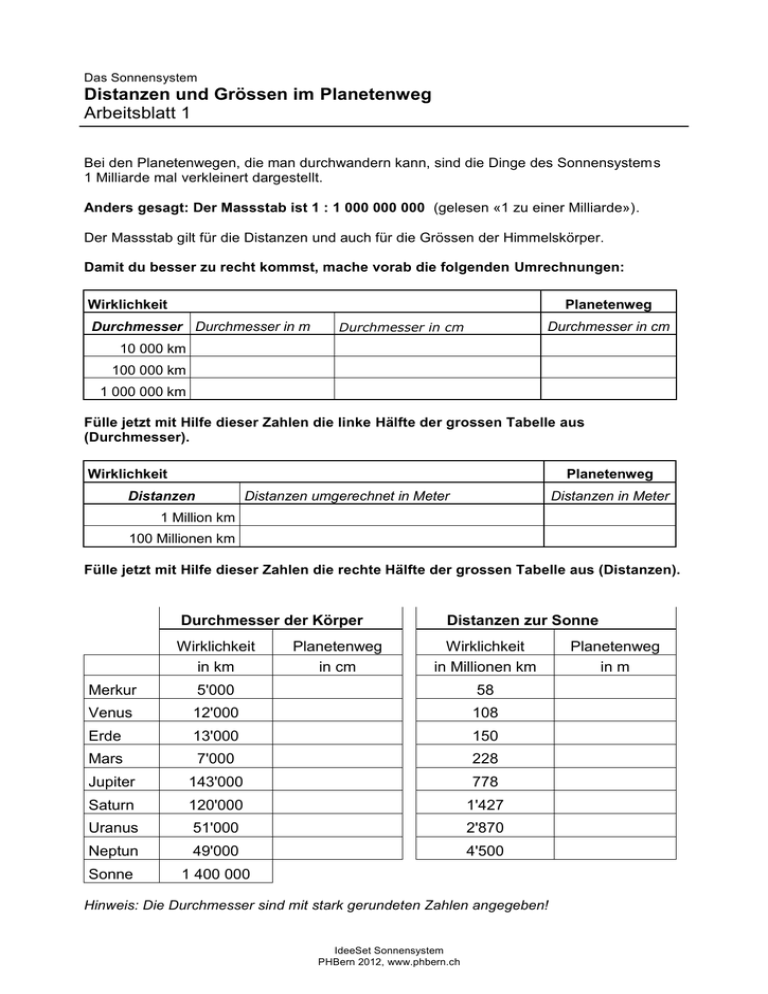
Das Sonnensystem Distanzen und Grössen im Planetenweg Arbeitsblatt 1 Bei den Planetenwegen, die man durchwandern kann, sind die Dinge des Sonnensystems 1 Milliarde mal verkleinert dargestellt. Anders gesagt: Der Massstab ist 1 : 1 000 000 000 (gelesen «1 zu einer Milliarde»). Der Massstab gilt für die Distanzen und auch für die Grössen der Himmelskörper. Damit du besser zu recht kommst, mache vorab die folgenden Umrechnungen: Wirklichkeit Planetenweg Durchmesser Durchmesser in m Durchmesser in cm Durchmesser in cm 10 000 km 100 000 km 1 000 000 km Fülle jetzt mit Hilfe dieser Zahlen die linke Hälfte der grossen Tabelle aus (Durchmesser). Wirklichkeit Planetenweg Distanzen Distanzen umgerechnet in Meter Distanzen in Meter 1 Million km 100 Millionen km Fülle jetzt mit Hilfe dieser Zahlen die rechte Hälfte der grossen Tabelle aus (Distanzen). Durchmesser der Körper Wirklichkeit in km Planetenweg in cm Distanzen zur Sonne Wirklichkeit in Millionen km Merkur 5'000 58 Venus 12'000 108 Erde 13'000 150 Mars 7'000 228 Jupiter 143'000 778 Saturn 120'000 1'427 Uranus 51'000 2'870 Neptun 49'000 4'500 Sonne 1 400 000 Hinweis: Die Durchmesser sind mit stark gerundeten Zahlen angegeben! IdeeSet Sonnensystem PHBern 2012, www.phbern.ch Planetenweg in m Das Sonnensystem Modell des Sonnensystems im Schulzimmer Arbeitsblatt 2 Bei den Planetenwegen, die man durchwandern kann, sind die Dinge des Sonnensystems 1 Milliarde mal verkleinert dargestellt. Die Tabelle unten auf dieser Seite enthält in den vorderen Kolonnen die Angaben zu einem solchen Planetenweg. Aufgabe: Plane ein Modell des Sonnensystems, welches an einer Wand in eurem Schulzimmer oder sonst irgendwo im Schulhaus Platz hat. Rechne für jeden Planeten aus, wie weit weg von der Sonne er in diesem Modell sein muss. Gehe so vor: 1. Miss, wie viel Platz für das Modell zur Verfügung steht. Schreibe diese Zahl in die Tabelle bei Neptun / Distanz zur Sonne (in der 4. Kolonne). 2. Rechne aus, wie oft mal kleiner diese Strecke ist als die entsprechende Distanz im Planetenweg (4500 m). Notiere hier: Das neue Modell wird ............................. mal kleiner als der Planetenweg. 3. Teile alle Distanzen des Planetenweges durch diese «Verkleinerungszahl», trage die Resultate in die 4. Kolonne der Tabelle ein. 4. Du kannst die Durchmesser von Sonne und Jupiter durch die «Verkleinerungszahl» teilen. Dabei wirst du sehr kleine Zahlen erhalten. Es ist nicht möglich, die Planeten so klein darzustellen. Man muss eine andere Möglichkeit suchen! Planetenweg Körper Modell im Klassenzimmer Durchmesser Distanz zur Sonne Distanz zur Sonne in cm in m in m Merkur 0.5 58 Venus 1.2 108 Erde 1.3 150 Mars 0.7 228 Jupiter 14 778 Saturn 12 1427 Uranus 5 2870 Neptun 5 4500 Sonne 140 l IdeeSet Sonnensystem PHBern 2012, www.phbern.ch Das Sonnensystem Die Geschwindigkeit der Planeten Arbeitsblatt 3 Die Planeten wandern ungefähr auf Kreisbahnen um die Sonne. Aufgabe 1: Rechne aus, wie gross die Geschwindigkeit der Planeten ist in Kilometer pro Sekunde. Beim Berechnen der fehlenden Zahlen in der Tabelle kommst du schrittweise zur Lösung. Schreibe stark gerundete Zahlen in die Tabelle (nicht alle Ziffern vom Taschenrechner)! Planet Distanz zur Sonne in Millionen km Bahnlänge Umlaufzeit in Millionen km in Tagen Merkur 58 88 Venus 108 225 Erde 150 365 Mars 228 687 Jupiter 778 4 333 Saturn 1 427 10 759 Uranus 2 870 30 685 Neptun 4 500 60 189 Strecke in 1 Tag Strecke in 1 Sek. Kontrolle: Die Geschwindigkeiten liegen zwischen 5 und 50 Kilometer / Sekunde. Jetzt kannst du folgende Frage beantworten: Weshalb haben die äusseren Planeten länger für einen Umlauf um die Sonne? (Es gibt zwei Gründe!) Aufgabe 2: Rechne für die Planeten Mars bis Neptun aus, wie viele Jahre und Tage ein Umlauf dauert. l IdeeSet Sonnensystem PHBern 2012, www.phbern.ch Das Sonnensystem Wie lang ist das Licht unterwegs? Arbeitsblatt 4 l– Damit wir die Gestirne sehen, muss Licht von ihnen ins Auge des Beobachters fallen. – Wir können angeben, wie lange das Licht von einem Stern bis zu uns unterwegs war. – Diese Zeit ist ein Mass für die Entfernung des Sterns. – Je weiter weg der Stern ist, desto länger ist das Licht unterwegs bis zu uns. Aus der Entfernung die Zeit berechnen oder umgekehrt Dies ist möglich, wenn man weiss, wie schnell ein Lichtstrahl läuft. Lichtgeschwindigkeit = 300 000 km/Sek. Aufgabe: Rechne, wie lange das Licht braucht von den Gestirnen bis zu uns. Rechne in Stunden und Minuten um, dort wo es sinnvoll ist. Objekt Entfernung Mond 384 000 km So lange braucht das Licht in Millionen km Sonne 150 Mars 55 Jupiter 600 Saturn 1'200 Uranus 2'600 Neptun 4'300 Für die Planeten sind die kleinsten Entfernungen angegeben, die möglich sind. Ausblick Die Himmelsobjekte ausserhalb unseres Sonnensystems sind unvorstellbar weit entfernt. Von ihnen braucht das Licht nicht einige Stunden, sondern viele Jahre, bis es bei uns ist. 1 Lichtjahr = Distanz, welche ein Lichtstrahl in einem Jahr zurücklegt Beispiele für Distanzen ausserhalb des Sonnensystems: Sirius, der hellste Stern 9 Lichtjahre Polarstern 400 Lichtjahre Stern Deneb im Schwan 3 000 Lichtjahre Andromeda-Galaxie 2 300 000 Lichtjahre IdeeSet Sonnensystem PHBern 2012, www.phbern.ch Das Sonnensystem Entfernungen der Planeten von der Sonne Arbeitsblatt 5 Zum Lösen dieser Aufgabe brauchst du Kenntnisse über Gleichungen und über Potenzen und Wurzeln. Der Astronom Johannes Kepler (1571-1630) hat in drei verschiedenen Gesetzen beschrieben, nach welchen Gesetzmässigkeiten die Planeten um die Sonne laufen. Das «3. Keplersche Gesetz» sagt: «Die Quadrate der Umlaufzeiten der Planeten verhalten sich wie die Kuben (3. Potenzen) ihrer mittleren Entfernungen zur Sonne». Anders formuliert: Teilt man das Quadrat der Umlaufzeit durch die 3. Potenz der Entfernung, erhält man bei jedem Planeten dasselbe Ergebnis. So wurde es damals möglich, aus den bekannten Umlaufzeiten die noch unbekannten Entfernungen der Planeten zu finden. Diese Berechnungen können wir hier – für alle Planeten – nachvollziehen. Man kann für die Distanz Erde-Sonne den Wert 1 einsetzen (1 Astronomische Einheit), so werden die Berechnungen erstaunlich einfach! Planet Umlaufzeit Quadrat der Distanz 3. Potenz Konstanter in Jahren Umlaufzeit in AE der Distanz Quotient T T2 R R3 T2 : R3 Merkur 0.241 Venus 0.615 Erde 1.000 Mars 1.881 Jupiter 11.860 Saturn 29.460 Uranus 84.012 Neptun 164.789 1 Gehe so vor: 1. Berechne vorab auf der Zeile «Erde» alle fehlenden Zahlen. 2. Fülle in der letzten Kolonne alle Felder aus. Nach dem 3. Keplergesetz muss hier überall dieselbe Zahl stehen! 3. Berechne den Wert T 2 für alle Planeten (3. Kolonne) 4. Berechne mit den Zahlen aus der 3. und 6. Kolonne die Werte für R 3. 5. Ziehe aus diesen Zahlen die Kubikwurzel, so erhältst du R für alle Planeten. 6. 1 Astronomische Einheit (1AE) = 149.6 Millionen km Kennt man diese Zahl, kann man leicht für alle anderen Planeten die Entfernung von der Sonne in Kilometern berechnen. IdeeSet Sonnensystem PHBern 2012, www.phbern.ch Das Sonnensystem Entfernungen der Planeten von der Sonne – Lösungen Arbeitsblatt 5 Lösungen Planet Umlaufzeit in Jahren Quadrat der Umlaufzeit Distanz in AE 3. Potenz Distanz Konstanter Quotient T T2 R R3 T2 : R3 Merkur 0.241 0.058081 0.387 0.058081 1 Venus 0.615 0.378225 0.723 0.378225 1 Erde 1.000 1 1.000 1 1 Mars 1.881 3.538161 1.524 3.538161 1 Jupiter 11.860 140.6596 5.201 140.6596 1 Saturn 29.460 867.8916 9.539 867.8916 1 Uranus 84.012 7058.016144 19.182 7058.016144 1 Neptun 164.789 27155.41452 30.057 27155.41452 1 Hinweis Die Distanz Erde-Sonne war noch recht ungenau bekannt, als Kepler seine Gesetze formulierte. Man hatte also zunächst für die Distanzen nur Verhältniszahlen – dafür aber sehr genaue! Viel später konnte man absolute Entfernungen – und damit auch die Grösse der AE – mit Hilfe von Radarmessungen (z.B. von der Erde zur Venus) sehr genau bestimmen. Heute gilt folgende Definition: 1 Astronomische Einheit ist der Radius einer kreisförmigen Umlaufbahn, auf der ein Objekt mit vernachlässigbarer Masse und frei von Störungen die Sonne in einem Jahr umläuft. Die AE beträgt 149.597.870.691 Meter. Die wahren Planetenbahnen In Wirklichkeit laufen die Planeten in elliptischen Bahnen um die Sonne (1. Keplergesetz), wobei die Bahn-Geschwindigkeit sich leicht ändert. Zur Vereinfachung haben wir auf allen Arbeitsblättern mit Kreisbahnen, mit einem mittleren Abstand von der Sonne und mit konstanten Umlaufgeschwindigkeiten gerechnet. IdeeSet Sonnensystem PHBern 2012, www.phbern.ch