Lichtgeschwindigkeit nach Römer

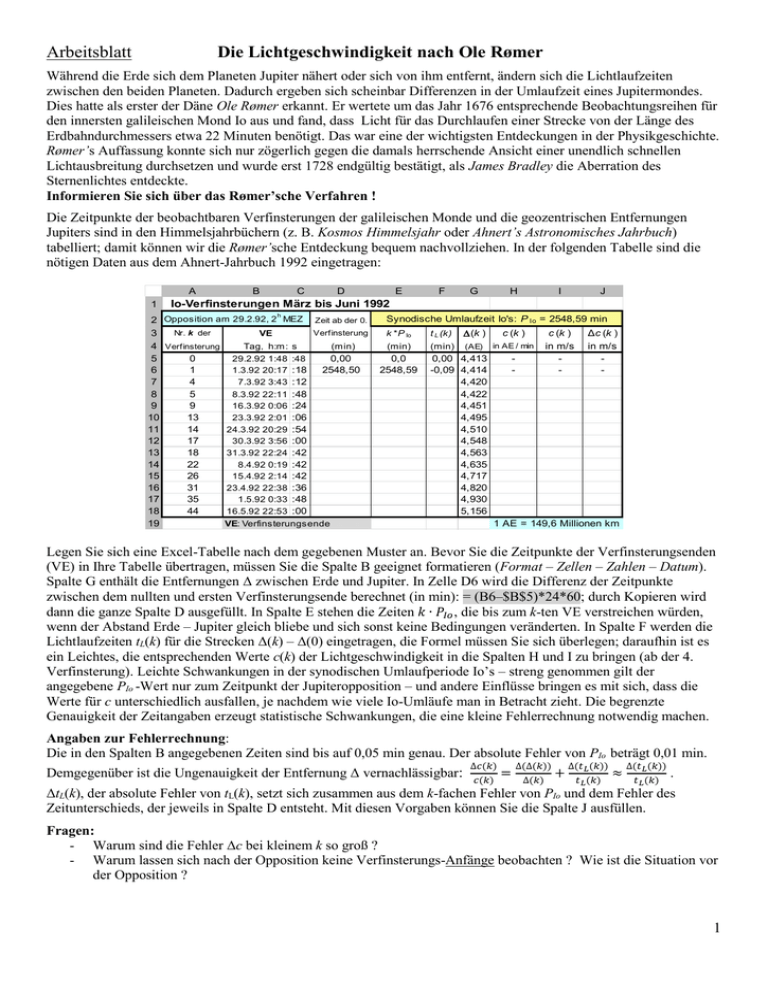
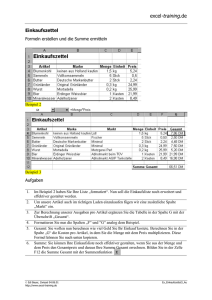
Arbeitsblatt
Die Lichtgeschwindigkeit nach Ole Rømer
Während die Erde sich dem Planeten Jupiter nähert oder sich von ihm entfernt, ändern sich die Lichtlaufzeiten
zwischen den beiden Planeten. Dadurch ergeben sich scheinbar Differenzen in der Umlaufzeit eines Jupitermondes.
Dies hatte als erster der Däne Ole Rømer erkannt. Er wertete um das Jahr 1676 entsprechende Beobachtungsreihen für
den innersten galileischen Mond Io aus und fand, dass Licht für das Durchlaufen einer Strecke von der Länge des
Erdbahndurchmessers etwa 22 Minuten benötigt. Das war eine der wichtigsten Entdeckungen in der Physikgeschichte.
Rømer’s Auffassung konnte sich nur zögerlich gegen die damals herrschende Ansicht einer unendlich schnellen
Lichtausbreitung durchsetzen und wurde erst 1728 endgültig bestätigt, als James Bradley die Aberration des
Sternenlichtes entdeckte.
Informieren Sie sich über das Rømer’sche Verfahren !
Die Zeitpunkte der beobachtbaren Verfinsterungen der galileischen Monde und die geozentrischen Entfernungen
Jupiters sind in den Himmelsjahrbüchern (z. B. Kosmos Himmelsjahr oder Ahnert’s Astronomisches Jahrbuch)
tabelliert; damit können wir die Rømer’sche Entdeckung bequem nachvollziehen. In der folgenden Tabelle sind die
nötigen Daten aus dem Ahnert-Jahrbuch 1992 eingetragen:
A
1
B
C
D
E
F
G
H
I
J
Io-Verfinsterungen März bis Juni 1992
h
2 Opposition am 29.2.92, 2 MEZ Zeit ab der 0.
Nr. k der
Verfinsterung
3
VE
4 Verfinsterung
Tag , h:m: s
(min)
5
0
29.2.92 1:48 :48
0,00
6
1
1.3.92 20:17 :18
2548,50
7
4
7.3.92 3:43 :12
8
5
8.3.92 22:11 :48
9
9
16.3.92 0:06 :24
10
13
23.3.92 2:01 :06
11
14
24.3.92 20:29 :54
12
17
30.3.92 3:56 :00
13
18
31.3.92 22:24 :42
14
22
8.4.92 0:19 :42
15
26
15.4.92 2:14 :42
16
31
23.4.92 22:38 :36
17
35
1.5.92 0:33 :48
18
44
16.5.92 22:53 :00
19
VE: Verfinsterungsende
Synodische Umlaufzeit Io's: P Io = 2548,59 min
k *P Io
t L (k)
D(k )
c (k )
(min)
(min)
(AE)
in AE / min
0,0
2548,59
0,00 4,413
-0,09 4,414
4,420
4,422
4,451
4,495
4,510
4,548
4,563
4,635
4,717
4,820
4,930
5,156
-
Δc (k )
in m/s
-
c (k )
in m/s
-
1 AE = 149,6 Millionen km
Legen Sie sich eine Excel-Tabelle nach dem gegebenen Muster an. Bevor Sie die Zeitpunkte der Verfinsterungsenden
(VE) in Ihre Tabelle übertragen, müssen Sie die Spalte B geeignet formatieren (Format – Zellen – Zahlen – Datum).
Spalte G enthält die Entfernungen Δ zwischen Erde und Jupiter. In Zelle D6 wird die Differenz der Zeitpunkte
zwischen dem nullten und ersten Verfinsterungsende berechnet (in min): = (B6‒$B$5)*24*60; durch Kopieren wird
dann die ganze Spalte D ausgefüllt. In Spalte E stehen die Zeiten 𝑘 ∙ 𝑃𝐼𝑜 , die bis zum k-ten VE verstreichen würden,
wenn der Abstand Erde ‒ Jupiter gleich bliebe und sich sonst keine Bedingungen veränderten. In Spalte F werden die
Lichtlaufzeiten tL(k) für die Strecken Δ(k) – Δ(0) eingetragen, die Formel müssen Sie sich überlegen; daraufhin ist es
ein Leichtes, die entsprechenden Werte c(k) der Lichtgeschwindigkeit in die Spalten H und I zu bringen (ab der 4.
Verfinsterung). Leichte Schwankungen in der synodischen Umlaufperiode Io’s – streng genommen gilt der
angegebene PIo -Wert nur zum Zeitpunkt der Jupiteropposition – und andere Einflüsse bringen es mit sich, dass die
Werte für c unterschiedlich ausfallen, je nachdem wie viele Io-Umläufe man in Betracht zieht. Die begrenzte
Genauigkeit der Zeitangaben erzeugt statistische Schwankungen, die eine kleine Fehlerrechnung notwendig machen.
Angaben zur Fehlerrechnung:
Die in den Spalten B angegebenen Zeiten sind bis auf 0,05 min genau. Der absolute Fehler von PIo beträgt 0,01 min.
∆𝑐(𝑘)
∆(∆(𝑘))
∆(𝑡 (𝑘))
∆(𝑡 (𝑘))
Demgegenüber ist die Ungenauigkeit der Entfernung Δ vernachlässigbar: 𝑐(𝑘) = ∆(𝑘) + 𝑡 𝐿(𝑘) ≈ 𝑡 𝐿(𝑘) .
𝐿
𝐿
ΔtL(k), der absolute Fehler von tL(k), setzt sich zusammen aus dem k-fachen Fehler von PIo und dem Fehler des
Zeitunterschieds, der jeweils in Spalte D entsteht. Mit diesen Vorgaben können Sie die Spalte J ausfüllen.
Fragen:
- Warum sind die Fehler Δc bei kleinem k so groß ?
- Warum lassen sich nach der Opposition keine Verfinsterungs-Anfänge beobachten ? Wie ist die Situation vor
der Opposition ?
1