Arbeitsblättern

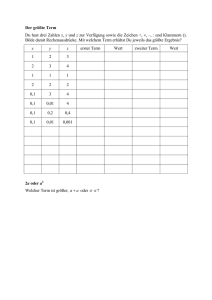
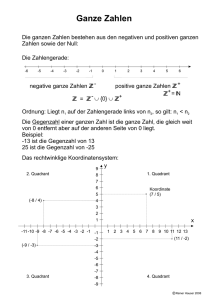
Leitidee Zahl: Umgehen mit Termen und Variablen
1. Wiederholung der Vorfahrtsregeln/Rechenreihenfolge bei Termen ohne VariableAufgabe
1: Berechne alle vier Terme schrittweise.
Terme/Rechenausdrücke werden
von links nach rechts berechnet!
a) 23 - 5 + 10
=
=
Klammern werden
zuerst berechnet!
Punkt- vor Strichrechnung!
b) 23 - (5 + 10)
=
=
c) 15 + 2 ∙ 5
=
=
d) 46 - 36 : 6
=
=
Aufgabe 2: Setze Klammern und Rechenzeichen so, dass das Ergebnis jedesmal 6 ist.
2
3
5
2
3
5
2
3
5
=
=
=
6
6
6
6
7
6
7
6
7
=
=
6
6
2. Wiederholung der Rechengesetze
Aufgabe 3: Berechne die Terme. Nutze die Rechenregeln zu deinem Vorteil bevor du rechnest.
Kommutativgesetz (Vertauschungsgesetz)
Asoziativgesetz (Verbindungsgesetz)
Distributivgesetz (Verteilungsgesetz)
=13 + 124 + 1050 + 37 + 76
= 4  ( 25 + 2222 )
=
=
=
=
=4  2  10  25  50
= 4  25 + 4  2222
=
=
=
=
Seite 1 von 5
Leitidee Zahl: Umgehen mit Termen und Variablen
3. Terme mit Variablen
Fachbegriffe:

Variable sind meist kleine Buchstaben (oder andere Symbole), die in Rechenausdrücken
stellvertretend für …………………………. stehen
Terme sind …………………………………………… mit Zahlen, Variablen und Rechenzeichen. Ersetzt
man die Variablen durch Zahlen, kann man den ………………………………… des Terms berechnen.
Terme sind äquivalent (gleichwertig), wenn ihre Werte bei jeder Ersetzung der
……………………… durch Zahlen gleich bleiben.


Aufgabe 4:
Setze in jeden Term für x = 2 und für y = 5 ein und berechne den Wert für jeden Term im Kopf.
Term
Wert
Term
Wert
Term
Wert
x+y
2x
x²
x-y
3y
y³
y +x
2x+3y
3∙ (x + y)
y-x
5xy
3x + 3y
Aufgabe 5:
Alexander behauptet: 3x + 4 = 7x
Überprüfe die Behauptung, indem du für x = 5 einsetzst.
Aufgabe 6:
Der Wert des folgenden Terms soll so nahe wie möglich bei 10 liegen.
Gib die natürliche Zahl an, die man dann für x einsetzen muss.
3 x 7
Aufgabe 7:
Ergebnis:
x = ...............
Kann man „Die Hälfte der Zahl a“ mit den folgenden Termen ausdrücken?
Setze für a eine gerade Zahl ein und überprüfe deine Entscheidungen.
a
2
a
1
2
ja
nein
ja
nein




a
ja
nein
0,5  a


1
a
2


a
2


a:
1
2


 Variable x die Zahl 3 einsetzt?
Aufgabe 8: Welcher Term erhält den Wert 50, wenn man für die
7  x 5
7  (x  5)
(7  x)  5
Seite 2 von 5
7 x  5
Leitidee Zahl: Umgehen mit Termen und Variablen
4. Einfache Sachsituationen und Terme mit Variablen einander zuordnen
Aufgabe 9: Gegeben sind die beiden Streckenlängen a und b.
a
b
a) Erstelle zu jeder Figur einen Term für die gesamte Streckenlänge.
a
a
a
b
a
a
a
b
b
a
b
b
Merke:
Eine Summe mit …………………………………………. Summanden,
schreibt man einfacher als ……………………………………………….
b) Erstelle zu jeder Figur einen Term für den Umfang.
b
a
a
a
a
u = …………
a
a
a
a
a
b
b
a
b
u = …………
u = …………
u = …………
c) Setze in die Terme, die du erstellt hast für die Variable a = 3 cm und für die Variable b = 5 cm ein
und berechne jeweils den Wert der Terme.
……………………………………
……………………………………
……………………………………
……………………………………
……………………………………
……………………………………
……………………………………
……………………………………
……………………………………
Seite 3 von 5
Leitidee Zahl: Umgehen mit Termen und Variablen
Aufgabe 10 :
Die drei Abbildungen zeigen kleine Pakete, große Pakete und Gewichte.
Die kleinen Pakete wiegen x kg, die großen y kg und die Gewichte 1 kg.
Erstelle jeweils einen Term für das abgebildete Gewicht.
y
x
x
x
x
y
x
1
x
1
x
x
1
x
Aufgabe 11 :
Erstelle einen Term für Gesamtlänge der Strecke.
4x
6y
8x
3y
Aufgabe 12:
Erstelle jeweils einen Term für den Umfang und den Flächeninhalt der Rechtecke.
2b
a
3a
a
3a + 5
3a + b
2b
a
2b
a
u=
u=
u=
A=
A=
A=
Aufgabe 13 :
In der Tabelle gehört zu jedem Text ein Term und umgekehrt. Erstelle zu jedem Text den
dazugehörigen Term und zu jedem Term den dazugehörigen Text.
Text
Das Doppelte einer Zahl
Term
5a
Der vierte Teil einer Zahl
a:2
Addiere 5 zu einer Zahl
b-5
Subtrahiere eine Zahl von 5
Addiere zum Dreifachen einer Zahl das Fünffache dieser Zahl
5x – 3x
Verdopple die Summe aus einer Zahl und 3
3∙(y+2)
Seite 4 von 5
y
Leitidee Zahl: Umgehen mit Termen und Variablen
Aufgabe 14: Erstelle mit Hilfe des Dreisatzprinzips zu jedem Text einen Term.
Text
Term
x
Preis für 1 kg Bananen
Preis für 5 kg Bananen
y
Preis für 50 Liter Benzin
Preis für 10 Liter Benzin
Preis für 1 Liter Benzin
Preis für 100 Liter Benzin
a
Alter von Peter
Karl ist 2 Jahre älter als Peter.
→ Alter von Karl
Maria ist 3 Jahre älter als Karl.
→ Alter von Maria
Ihre Mutter ist doppelt so alt wie Maria.
→ Alter der Mutter
Ihr Vater ist 4 Jahre älter wie die Mutter.
→ Alter des Vaters.
Die Oma ist so alt wie Vater und Mutter zusammen. →Alter der Oma.
Seite 5 von 5