EvolutionsstrategieN AngewandT AuF DeN MultI GravitY

Evolutionsstrategien für das
Multi Gravity Assist Problem
Ein Vergleich mehrerer Evolutionsstrategien angewandt
auf das Cassini-Problem des Multi Gravity Assist Problems
© 2009, Gruber Andy
TU Wien
Inhalt
•
EINLEITUNG
•
EVOLUTIONÄRE ALGORITHMEN
•
MULTI GRAVITIY ASSIST
•
ERGEBNISSE
Einleitung
[Abb 1]
Terminologie

Individuum
◦ Kandidatenlösung. Meist binär oder reell kodierter Vektor

Gen
◦ Eine Stelle des Vektors

Allel
◦ Ausprägung einer Stelle des Vektors

Population
◦ Menge von Individuen

Offspring
◦ Erzeugte Nachkommen
Evolutionäre Algorithmen
Metaheuristik
 Optimierungsverfahren
 Arbeitet mit Population von Kandidatenlösungen
 Relativ robustes Verfahren


Bestandteile eines EAs:
 Rekombination
 Mutation
 Selektion

Nicht bei allen EAs vorhanden
Drei Hauptvertreter:
 Evolutionäres Programmieren
 Genetische Algorithmen
 Evolutionsstrategien
Evolutionäre Algorithmen (2)

Formale Definition:
EA = (I ,Φ ,Ω , s ,ι ,μ ,λ)
◦ Suchraum
◦ Fitnessfunktion
◦ Genetische Operatoren
◦ Selektionsoperator
◦ Abbruchkriterium
◦ Parents
◦ Offsprings
Entnommen aus Evolutionary Algorithms in Theory and Practise, Thomas Bäck
Evolutionäre Algorithmen (3)

Formaler Ablauf:
initialisiere(Eltern);
werte_Aus(Eltern);
while(Abbruchkriterium nicht erfüllt)
rekombiniere(Eltern, Kinder);
mutiere(Kinder);
werte_Aus(Kinder);
selektiere(Kinder,Eltern);
do
Biologischer Hintergrund
1856 Charles Darwin - Evolutionstheorie
 1865 Gregor Mendel - Vererbung


DNA kodiert
Erbinformationen

Variationsfaktoren:
◦ Rekombination(Meiose)
◦ Mutation(Fehler bei Meiose)
[Abb 2]
Evolutionäres Programmieren

Lawrence J. Fogel 1960

Struktur eines EP nicht genau definiert

Jedes Individuum wird als eigene Spezies angesehen
◦ Daher (im Normalfall) keine Rekombination

Anfangs: Voraussagen von Bitfolgen mittels Endliche
Automaten, welche durch Mutation und Selektion optimiert
wurden.
Genetische Algorithmen
Holland und Goldberg um 1970
 DNA wird als [0,1]-Folge betrachtet
 Rekombination wichtiger als Mutation

◦ Mutation: Eine Stelle wird invertiert

Crossover erzeugt neue/zerstört alte Schemata
Gutes Schema
Individuum
Bevorzugter Crossoverpunkt
Suboptimaler Crossoverpunkt
Evolutionsstrategien

Rechenberg und Schwefel 1960

Individuen reell kodiert

Mutation primärer Operator
◦ Oft in Kombination mit Anpassung der Strategieparameter

Rekombination sekundär (teilw. weggelassen)
◦ (1+1)ES – keine Rekombination
ES vs. GA

GA
Int
Bin
Gray
◦ Binär kodiert
0
000
000
◦ Eher für kombinatorische Probleme geeignet
1
001
001
2
010
011
3
011
010
4
100
110
5
101
111
◦ Setzt auf Rekombination
◦ Hamming-Klippe → Gray Code

ES
◦ Reell kodiert
◦ Gut geeignet für kontinuierliche
Optimierungsprobleme
◦ Setzt auf Mutation
[Abb 3]
Rekombinationsarten

Crossover:
Genau ein Rekombinationsstelle wischen zwei
benachbarten Genen

Uniform Crossover:
Verallgemeinerte Version
des Standard Crossovers.
1 – (n-1) Rekombinationsstellen, wobei n die Anzahl
der Gene
Rekombinationsarten (2)

Panmictic discrete:
Ein Parent wird gehalten und zufällig dieser oder ein zufälliger anderer
Parent für jedes Gen ausgewählt

Intermediate:
Offspring besteht aus
Mittelwerten der einzelnen
Gene der Eltern
Rekombinationsarten (3)

Generalized intermediate:
Wie Intermediate, nur werden die Eltern zufällig gewichtet
Bsp:
O[i] = P1[i] * r + P2[i] * (1-r), r = U(0,1)

Panmictic generalized intermediate:
Ein Parent wird festgehalten und für jedes Gen wird zufällig ein zweiter
ausgewählt und von diesen beiden der gewichtete Durchschnitt
genommen.
Mutationsarten

U(0,σ)
 Auf jedes Allel eines Individuums wird eine uniform verteilte Zufallszahl
addiert/subtrahiert
 Konvergenzgeschwindigkeit nicht adäquat
 Zerstört häufig „gute“ Individuen bzw. „vergisst“ gute Bereiche
 „Breiter gefächerte“ Suchraumabdeckung

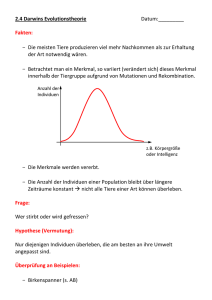
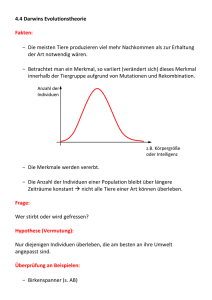
N(0,σ)
 Gute Individuen, sowie gute Bereiche werden beibehalten
 Wie in Natur → Kleinere Abweichungen häufiger als große
 Präzisere Suchraumabdeckung
 Tendiert eher dazu in lokalen Optima hängen zu bleiben
Strategieparameteranpassung

Schnellere und gezieltere Konvergenz in Richtung Optimum
[Abb 4]

1 Strategieparameter (σ)
 1/5 Regel (Rechenberg): Zu statisch und zu allgemein

n Strategieparameter
 Für jedes Gen eines Individuums wird ein σ mitgeführt

(n²+n) / 2 Strategieparameter - CMA-ES
 Pro Individuum wird eine (Korrelations-)Rotationsmatrix mitgeführt
Strategieparameteranpassung (2)

N Strategieparameter:
◦ Werden mit rekombiniert
◦ Schwefel empfiehlt folgende Werte:
τ α ( √(2 √(n) )-1
τʹ α ( √(2n) )-1
→
→
[0,1]
[0,1]
◦ In der Praxis werden meist für τ und τʹ = 1 eingesetzt
σi‘ = σi * exp( τ’ * N(0,1) + τ * Ni(0,1) )
xi‘ = xi + σi‘ * Ni(0,1)
◦ τ und τʹ Lernfaktoren
Strategieparameteranpassung (3)

CMA-ES
◦ N Strategieparameter + Rotationsmatrix pro Individuum
◦ Rotationsmatrix wird mit jeder Generation aktualisiert
◦ „Lernt“ die paarweisen Abhängigkeiten zwischen zwei Variablen
◦ Mutation wird nicht nur auf Achsenrichtungen beschränkt
◦ Gezielteres „abtasten“ des Suchraumes
Selektionsarten

Selektionsdruck
 Quotient aus (Anzahl Kinder)/(Anzahl Eltern)

ES(µ+λ)
 Nächste Generation wird durch λ besten Individuen aus Eltern und
Offspring gebildet. → Fitnesswerte monoton fallend.
 Spezialfall (1+1): Keine Rekombination
Selektionsarten (2)

ES(µ,λ)
 Nächste Generation wird durch λ besten Individuen aus Offspring
gebildet. → Fitnesswerte nicht unbedingt monoton fallend.
(Multi) Gravity Assist
[Abb 5]

Ausnutzen der Gravitation in Kombination
mit der Bewegung eines Planeten

Beschleunigung/Verlangsamung möglich

Energieerhaltungssatz → Raumsonde
behält Geschwindigkeit relativ zum
Planeten.

Mehrfaches Ausnutzen dieses Effektes
nennt man multi gravity assist
GTOP: Cassini/Huygens Problem

Flugbahn E-V-V-E-J-S
◦ Mittels gravity assists zu lösen
◦ Deep space maneuver wird
vernachlässigt

Minimieren des Δv
Budgets
◦ Summe des Aufwandes der
nötigen Impulse zur Änderung
der Geschwindigkeit
[Abb 6]
GTOP: Global Optimization
Trajectory Problems and Solutions

GTOPtoolbox:
◦ Auf der Homepage der ESA erhältlich
◦ „Wettbewerb“
◦ C++ Framework
◦ Enthält mehrere Problemstellungen, in denen es gilt Flugbahnen von
Raumsonden zu optimieren
◦ Darunter auch das Cassini-Problem
 double cassini1(const std::vector &x,
std::vector& rp)
rp1 > 6351.8 km
rp2 > 6351.8 km
rp3 > 6778.1 km
rp4 > 671492 km
Implementierung

OOP in C++
 Pro: Anpassung der Strategieparameter einfacher
 Kontra: Rechen/Laufzeit höher

Individuum
 Double Values[6]
 Double stdDev[6]
 Double Fitness



Verschiedene Rekombinationsarten
(µ,λ), sowie (µ + λ)
Variationsparameter können „zur Laufzeit“ verstellt
werden
Probleme

Lokale Optima
◦ Wie gelangt man wieder heraus?
◦ Ist es schon das globale Optimum?

Suchraumabdeckung
◦ Gezielte, minimal erforderliche Suchraumabdeckung erwünscht

Welche Strategie ist optimal für diese Problemstellung?
Messergebnisse

Parameter:
Strategie
Sel
Best
AVG
Dev
t/Gen[s]
◦ 20 Eltern
No recombination
,
5,68310
7,04252
2,57920
0,1
◦ 100 Kinder
No recombination
+
5,90280
6,98327
1,02741
0,17
◦ 1000
Generationen
Crossover
,
5,20242
5,33467
0,10400
1,795
Crossover
+
5,30392
5,46430
0,29342
1,767
◦ 30 Runs
Uniform Crossover
,
5,06380
6,02480
2,26461
0,659
◦ 10 Initiale
Uniform Crossover
+
5,18885
5,37967
0,19311
0,631
StdDev
Panmictic discrete
,
5,30571
6,01289
1,56185
1,785
Panmictic discrete
+
5,30480
5,92314
0,46828
1,746
Generalized Intermediate
,
5,31651
6,12639
1,34027
0,637
Generalized Intermediate
+
5,14089
5,83976
0,25157
0,616
Panmictic generalized intermediate
,
5,31560
10,9193
2,68076
0,650
Panmictic generalized intermediate
+
5,30850
5,44183
0,28221
0,643
Bestes Ergebnis

Reproduzierbar mit ES(1000,200) nach 800
Generationen:
◦ 4,9656
◦ {-789.229, 155.339, 449.385, 56.252, 1006.671, 4523.828}

Aktuell weltweit bester erreichter Wert:
◦ 4,9307
◦ {-789.812, 158.302, 449.385, 54.748, 1024.362, 4552.307}

Papanek Martin:
◦ PSO: 4.95223
◦ DE mit NM: 4.93071
Andere versuchte Ansätze

ES(µ,λ) zusammen mit k besten Eltern
 Keine signifikante Verbesserung
 Minimal bessere Konvergenz

N(0,µ), wobei µ = Elter[1].val – Elter[2].val
 Keine merkbare Verbesserung
 Werte in der „Mitte“ häufen sich im Verlauf der Generationen

ES(µ,λ) mit k besten Kindern
 Zusätzlich zu den λ-k besten Individuen aus dem Offspring werden die k
fittesten Individuen aus dem Offspring gewählt
Andere versuchte Ansätze (2)

Primitive lokale Optimierung nach EA
 Sehr rechenintensiv
 Schnellere Konvergenz
 Lokale Verbesserungen aber schlussendlich selbe Ergebnisse

% zufällig ausgewählte Kinder
 Keine feststellbare Verbesserung
 Größere Streuung der Fitnesswerte am Anfang
Weitere mögliche Ansätze

Hybrider Ansatz
◦ ES mit einer Lokalen Suchstrategie kombinieren

Linear ranking
◦ Individuen werden ihres Fitnesswerts nach geordnet
◦ Die Wahrscheinlichkeit der Selektion ist proportional zu dessen Rang

Nicht alle Individuen rekombinieren
◦ Nur einen großen Teil (zb. 80%) rekombinieren, Rest direkt
übernehmen
Weitere mögliche Ansätze (2)

Tournament selection
◦ K zufällige Individuen auswählen und das beste davon selektieren

Individuen überleben nur k Generationen
◦ Lebenszeit eines Individuums wird nach jeder Generation
dekrementiert

Search space pruning
◦ Individuen oder ganze Bereiche innerhalb des Suchraumes
ausschließen, da sie „unmöglich“ sind
Erkenntnisse

Populationsgröße nicht unwichtig, aber Anzahl von Generationen
wichtiger → Variationsfaktoren haben großen Einfluss auf die
Ergebnisse

Zu viele Einschränkungen können einen guten Algorithmus
verschlechtern → Z.B. Ständiges Überprüfen auf Duplikate
vernachlässigen.
Referenzen

[Abb 1] http://www.ngcsu.edu/academic/sciences/physics/jones/astr1010home/trajectory_lg.gif

[Abb 2] http://ocw.mit.edu/NR/rdonlyres/Biology/7-A12Fall-2005/D4134A30-F348-4615-8B0AD0CB5ED86081/0/chp_dna.jpg

[Abb 3] Folien Heuristische Optimierungsverfahren WS08, Raidl/Chwatal

[Abb 4] Evolutionary Programming in Theory and Practise, Thomas Bäck

[Abb 5] http://www.math.ubc.ca/~cass/courses/m308/projects/lim/images/Slingshot4.GIF

[Abb 6] http://www.raumfahrer.net/multimedia/4images/details.php?image_id=1792

Allgemein:

MGA – Cassini-Problem: http://www.esa.int/gsp/ACT/inf/op/globopt/evvejs.htm

Evolutionary Programming in Theory and Practise, Thomas Bäck

Folien Heuristische Optimierungsverfahren WS08, Raidl/Chwatal
Danke für die Aufmerksamkeit
Fragen oder Anregungen?