Power-Point Oberfläche Volumen
Werbung

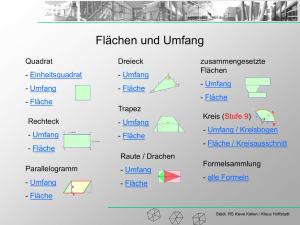
Körperberechnung Würfel Pyramide - Einheitswürfel - Oberfläche - Oberfläche - Volumen - Volumen Kegel Quader - Oberfläche - Oberfläche - Volumen - Volumen Kugel - zusammengesetzte Körper Prisma Zylinder -Oberfläche -Oberfläche -Volumen -Volumen - Oberfläche - Volumen Städt. RS Kleve Kellen / Klaus Hoffstadt Einheitswürfel Ein Einheitswürfel ist ein Würfel, bei dem jede Kante 1 cm lang ist. Sein Volumen ist definiert mit: 1 cm V = 1 [cm3] 1 cm 1 cm Bei der Volumenberechnung der folgenden Körper besteht die Idee immer darin, zu überprüfen, wie viele Einheitswürfel in den Körper passen. Beispiel: In einen Körper passen 35 Einheitswürfel. Dann gilt für sein Volumen: V = 35 · 1 [cm3] = 35 [cm3] Städt. RS Kleve Kellen / Klaus Hoffstadt Oberfläche Würfel Die Oberfläche eines Würfels besteht aus 6 Quadraten. Für die Fläche eines Quadrates gilt: A = a2 Also gilt für die Oberfläche des Würfels: O = 6 · a2 Städt. RS Kleve Kellen / Klaus Hoffstadt Volumen Würfel Wir überlegen, wie viele Einheitswürfel in einen Würfel mit einer Kantenlänge von a cm passen? Auf dem Boden des Würfels kann man „a – viele“ Würfel in eine Reihe legen. Von diesen Würfelreihen kann man „a – viele“ Reihen nebeneinander legen. Damit hat man „a2 – viele“ Einheitswürfel auf dem Boden liegen. Von den Würfelplatten passen „a – viele“ Platten übereinander. Also passen „a3 – viele“ Einheitswürfel in den großen Würfel. a cm a cm a cm Somit gilt: V = a3 Städt. RS Kleve Kellen / Klaus Hoffstadt Oberfläche Quader Die Oberfläche eines Quaders besteht aus 6 Rechtecken, von denen je zwei gleich groß sind. c cm b cm a cm Damit gilt für die Oberfläche: a cm O=2·a·b+2·a·c+2·b·c c cm bzw.: O = 2 · (a · b + a · c + b · c) b cm c cm b cm Städt. RS Kleve Kellen / Klaus Hoffstadt Volumen Quader Wir überlegen, wie viele Einheitswürfel in einen Quader mit den Kantenlängen a cm, b cm und c cm passen? Auf dem Boden des Quaders kann man „a – viele“ Würfel in eine Reihe legen. Von diesen Würfelreihen kann man „b – viele“ Reihen nebeneinander legen. Damit hat man „a · b – viele“ Einheitswürfel auf dem Boden liegen. Von den Würfelplatten passen „c – viele“ Platten übereinander. Also passen „a · b · c – viele“ Einheitswürfel in den großen Würfel. Somit gilt: V = a · b · c Städt. RS Kleve Kellen / Klaus Hoffstadt Zusammengesetzte Körper Um zusammengesetzte Körper zu berechnen, muss man sie in die einzelnen Teilkörper zerlegen und diese einzeln berechnen. Volumen: V1 Man addiert bzw. subtrahiert das Volumen der einzelnen Teilkörper und erhält so das Volumen des ganzen Körpers. V3 V = V1 + V2 bzw. V = V3 – V4 V2 Oberfläche: V4 Man addiert bzw. subtrahiert die Oberflächen der einzelnen Teilkörper. Achtung: Flächen, die sich überdecken dürfen nicht mit berechnet werden! Städt. RS Kleve Kellen / Klaus Hoffstadt Oberfläche Prisma Ein Prisma besteht aus zwei Grundflächen (hier Dreiecke) und einer Mantelfläche. Zerschneidet man ein Prisma und breitet es aus, entsteht ein sogenanntes Netz. Für die Darstellung eines solchen Netzes gibt es immer verschiedene Möglichkeiten (hier 9). In den Darstellungen 6 bis 9 erkennt man, dass die Mantelfläche ein Rechteck bildet. Städt. RS Kleve Kellen / Klaus Hoffstadt Oberfläche Prisma Die Breite der rechteckigen Mantelfläche entspricht der Höhe h des Prismas. Die Länge der Mantelfläche entspricht dem Umfang u der Grundfläche. Also gilt: h M = u · h und O = 2 · G + M Daraus folgt: O = 2 · G + u · h Städt. RS Kleve Kellen / Klaus Hoffstadt Volumen Prisma Um das Volumen zu bestimmen, füllen wir das Prisma wieder mit Einheitswürfeln. Dazu berechnet man zuerst, die Größe der Grundfläche G. Damit weiß man, wie viele Einheitswürfel auf die Grundfläche passen. h h In das Prisma passen „h – viele“ Würfelplatten übereinander. Somit kennt man die Anzahl aller Einheitswürfel, die in das Prisma passen. Es gilt also: V = G · h Städt. RS Kleve Kellen / Klaus Hoffstadt Oberfläche Zylinder Wenn man einen Zylinder mit der Höhe h zerlegt, erhält man zwei Kreise mit Radius r und eine Mantelfläche in Form eines Rechteck. Es gilt also: O = 2 · · r2 + M Das Rechteck hat die Höhe des Zylinders und seine Länge entspricht dem Umfang des Kreises. Folglich gilt: M = 2 · · r· h Daraus folgt durch Einsetzen: O = 2 · · r2 + 2 · · r · h bzw.: O = 2 · · r · (r + h) Städt. RS Kleve Kellen / Klaus Hoffstadt Volumen Zylinder Um das Volumen zu bestimmen, füllen wir den Zylinder wieder mit Einheitswürfeln. Die Grundfläche G eines Zylinders ist ein Kreis. Für sie gilt: G = · r2 Also kann man auf die Grundfläche „ · r2 – viele“ Einheitswürfel stellen. Von diesen Würfelplatten kann man „h – viele“ übereinander stapeln. Somit passen in den ganzen Zylinder „ · r2 · h – viele“ Einheitswürfel. Folglich gilt: V = · r2 · h Städt. RS Kleve Kellen / Klaus Hoffstadt Oberfläche der Pyramide Für jede Pyramide gilt: O = G + M Eine Pyramide mit quadratischer Grundfläche hat vier gleiche Dreiecke als Mantelfläche. Daher gilt hier: O = a2 + 4 · ½ · a · ha = a2 + 2 · a · ha ha Zwischen ha und G, s und G, und s und a liegen die Winkel , und . Sie können über die trigonometrischen Funktionen bestimmt werden. Die fehlenden Seiten berechnet man über den Pythagoras. Städt. RS Kleve Kellen / Klaus Hoffstadt Satz von Cavalieri (nach Bonaventura Cavalieri 1598 - 1647) Werden zwei Körper, die auf der selben Ebene stehen von allen dazu parallelen Ebenen in gleich großen Flächen geschnitten, so haben diese Körper das gleiche Volumen. Pyramiden mit gleich großer Grundfläche und gleicher Höhe haben gleiches Volumen. Städt. RS Kleve Kellen / Klaus Hoffstadt Volumen der Pyramide Baut man um eine Pyramide mit der Grundfläche G einen Quader mit der Höhe h, so gilt: VQ = G · h Nach Cavalieri sind beide Pyramiden gleich groß! Städt. RS Kleve Kellen / Klaus Hoffstadt Volumen der Pyramide Die neue Pyramide kann in zwei gleich große Pyramiden geteilt werden (nach Cavalieri). Städt. RS Kleve Kellen / Klaus Hoffstadt Volumen der Pyramide Unabhängig von der Höhe des Quaders sind alle drei Pyramiden gleich groß, da man sie alle in die beiden gleichen Teilpyramiden unterteilen kann. Städt. RS Kleve Kellen / Klaus Hoffstadt Volumen der Pyramide Das Volumen des Quaders ist also so groß, wie das Volumen von drei Pyramiden. Umgekehrt entspricht das Volumen einer Pyramide 1/3 des Volumens des Quaders. Damit gilt: V = 1/3 · G · h Städt. RS Kleve Kellen / Klaus Hoffstadt Oberfläche des Kegels Für die Oberfläche gilt wieder: O = G + M Die Grundfläche ist ein Kreis mit Radius r und die Mantelfläche ist ein Kreisausschnitt mit dem Winkel und dem Radius s. Der Umfang des Grundflächenkreises entspricht dem Kreisbogen der Mantelfläche. Daraus ergibt sich: O = · r 2 + · r · s Für gilt: = r/s · 360° Städt. RS Kleve Kellen / Klaus Hoffstadt Oberfläche des Kegels Warum gilt aber M = · r · s und warum gilt = r/s · 360° ??? M ist ein Kreisausschnitt. Für den ganzen Kreis gilt: M = · s 2 Für den Kreisausschnitt gilt also M = ( · s 2 · )/360° Für den Kreisbogen gilt b = (2 · · s · )/360° und b = 2 · · r Durch gleichsetzten ergibt sich 2 · · r = (2 · · s · )/360° Daraus folgt: = r/s · 360° Durch einsetzen in M = ( · s 2 · )/360° ergibt sich M = · r · s Städt. RS Kleve Kellen / Klaus Hoffstadt Volumen Kugel Jede Halbkugel besitzt einen umbeschriebenen Zylinder, dem wiederum ein Kegel einbeschrieben ist. Man kann nachweisen, dass nach Ausbohrung des Kegels aus dem Zylinder der Restkörper zur Halbkugel volumengleich ist. Nach Cavalieri muss dazu stets die Schnittfläche A1 des linken Körpers gleich der Schnittfläche A2 des rechten sein. Städt. RS Kleve Kellen / Klaus Hoffstadt Volumen Kugel Jeder Ring um den Zylinder soll die gleiche Fläche haben wie der entsprechende Kreis in der Halbkugel! Es muss also gelten: r2 - rz2 = rk2 Nach Strahlensatz gilt: rz/r = x/r x = rz x2 = rz2 | + r2 – x2 r2 = r2 - x2 + rz2 da gilt: rk2 = r2 - x2 r2 = rk2 + rz2 | - rz2 r2 - rz2 = rk2 |· (r2 - rz2) = rk2 q.e.d. Städt. RS Kleve Kellen / Klaus Hoffstadt Volumen Kugel Die Behauptung stimmt also und somit sind die jeweiligen Schnittflächen gleich. Da die Grundflächen und die Höhen ebenfalls gleich sind, sind nach Cavalieri auch die Volumen gleich. 2 · VH = 2 ·( · r3 – 1/3 · · r2 · r) 2 · VH = 2 ·(2/3 · · r3) V = 4/3 · · r3 Städt. RS Kleve Kellen / Klaus Hoffstadt Oberfläche Kugel Die Idee der Oberflächenberechnung besteht darin, die Kugel mit kleinen Pyramiden auszufüllen. Die Höhen der Pyramiden entsprechen dem Radius der Kugel. Je kleiner man die Pyramiden macht, um so genauer nähert sich die Grundflächen der Pyramiden der Oberfläche der Kugel an. Die Summe aller Grundflächen entspricht dann näherungsweise der Oberfläche der Kugel: (G1 + G2 + ... + Gn) = O Das Volumen der Kugel stimmt auch immer genauer mit dem Volumen aller Pyramiden überein. Städt. RS Kleve Kellen / Klaus Hoffstadt Oberfläche Kugel Für die Pyramiden gilt: V = 1/3 · G1 · r + 1/3 · G2 · r + ... + 1/3 · Gn · r V = 1/3 · r (G1 + G2 + ... + Gn) Für die Kugel gilt: V = 4/3 · · r3 Nach der Idee des „Annäherung“ der Grundflächen der Pyramiden an die Oberfläche der Kugel gilt folglich: 1/3 · r · (G1 + G2 + ... + Gn) = 4/3 · · r3 1/3 · r · O = 4/3 · · r3 |·3:r O = 4 · · r2 Städt. RS Kleve Kellen / Klaus Hoffstadt