Flächen- & Umfangformeln: Geometrie Spickzettel
Werbung
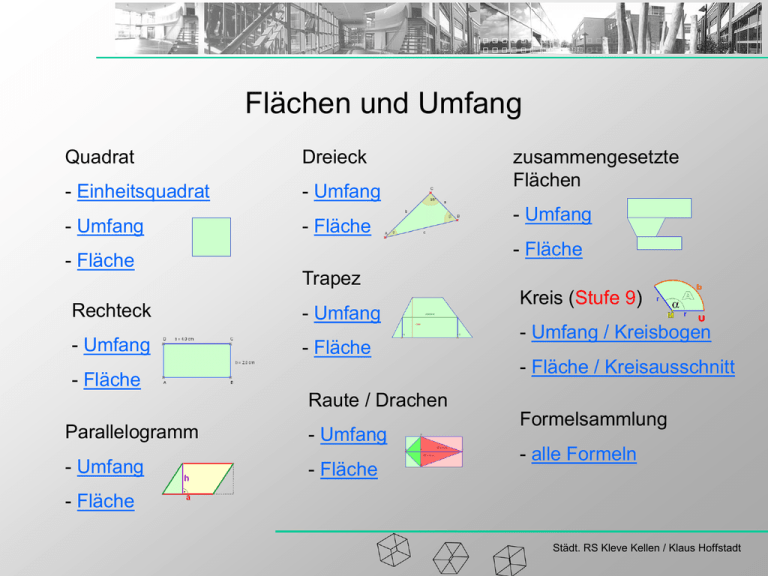
Flächen und Umfang Quadrat Dreieck - Einheitsquadrat - Umfang - Umfang - Fläche zusammengesetzte Flächen - Umfang - Fläche - Fläche Trapez Rechteck - Umfang - Umfang - Fläche Kreis (Stufe 9) - Umfang / Kreisbogen - Fläche / Kreisausschnitt - Fläche Raute / Drachen Parallelogramm - Umfang - Umfang - Fläche Formelsammlung - alle Formeln - Fläche Städt. RS Kleve Kellen / Klaus Hoffstadt Einheitsquadrate Ein Einheitsquadrat ist ein Quadrat, bei dem jede Kante 1 cm lang ist. Sein Fläche ist definiert mit: 1 cm A = 1 [cm2] 1 cm Bei der Flächenberechnung der folgenden Flächen besteht die Idee immer darin, zu überprüfen, wie viele Einheitsquadrate in die Fläche passen. Beispiel: In eine Fläche passen 35 Einheitsquadrate. Dann gilt für seine Fläche: A = 35 · 1 [cm2] = 35 [cm2] Städt. RS Kleve Kellen / Klaus Hoffstadt Umfang Quadrat a cm Bei einem Quadrat sind alle Seiten gleich lang und stehen im rechten Winkle zueinander. Da der Umfang die Summe aller Seitenlängen ist, gilt: a cm a cm a cm u = a + a + a + a bzw. u = 4 · a Städt. RS Kleve Kellen / Klaus Hoffstadt Fläche Quadrat Wir überlegen, wie viele Einheitsquadrate in ein Quadrat mit einer Seitenlänge von a cm passen. In einer Reihe kann man „a – viele“ Einheitsquadrate legen. Von diesen Reihen aus Einheitsquadraten kann man „a – viele“ Reihen übereinander legen. Also passen in das große Quadrat „a2 – viele“ Einheitsquadrate. a cm a cm Somit gilt: A = a2 Städt. RS Kleve Kellen / Klaus Hoffstadt Umfang Rechteck b cm Bei einem Rechteck sind die gegenüberliegenden Seiten gleich lang und parallel. Die Winkle sind rechtwinklig. Da der Umfang die Summe aller Seitenlängen ist, gilt: a cm a cm b cm u = a + b + a + b bzw. u = 2 · a + 2 · b bzw. u = 2 · (a + b) Städt. RS Kleve Kellen / Klaus Hoffstadt Fläche Rechteck Wir überlegen, wie viele Einheitsquadrate in ein Rechteck mit den Seitenlängen a cm und b cm passen. In einer Reihe kann man „a – viele“ Einheitsquadrate legen. Von diesen Reihen aus Einheitsquadraten kann man „b – viele“ Reihen übereinander legen. Also passen in das große Quadrat „a · b – viele“ Einheitsquadrate. b cm a cm Somit gilt: A = a · b Städt. RS Kleve Kellen / Klaus Hoffstadt Umfang Parallelogramm Beim Parallelogramm sind die gegenüberliegenden Seiten parallel und gleich lang. Die gegenüberliegenden Winkle sind gleich groß. Da der Umfang die Summe aller Seitenlängen ist, gilt: a cm b cm b cm a cm u = a + b + a + b bzw. u = 2 · a + 2 · b bzw. u = 2 · (a + b) Städt. RS Kleve Kellen / Klaus Hoffstadt Fläche Parallelogramm Ab jetzt überprüfen wir nicht mehr direkt, wie viele Einheitsquadrate in die Fläche passen, sondern formen die neue Fläche in bereits bekannte, gleich große Flächen um! Man kann ein Parallelogramm mit der Höhe h in ein Rechteck umformen. Man schneidet das „überstehende“ Dreieck ab und legt es an der gegenüberliegenden Seite des Parallelogramms wieder an. So entsteht ein Rechteck mit der Höhe des Parallelogramms. h a cm b cm Somit gilt: A = a · ha ; A = b · hb Städt. RS Kleve Kellen / Klaus Hoffstadt Umfang Dreieck Bezüglich der Winkel eines Dreiecks unterscheidet man zwischen rechtwinkligen, spitzwinkligen und stumpfen Dreiecken. Bezüglich der Seiten eines Dreiecks unterscheidet man zwischen gleichschenkligen und gleichseitigen Dreiecken. Für alle Dreiecke ist der Umfang gleich der Summe aller Seitenlängen. c cm b cm a cm Es gilt: u = a + b + c Städt. RS Kleve Kellen / Klaus Hoffstadt Fläche Dreieck Man kann mit jedem Dreieck ein Parallelogramm erstellen, welches doppelt so groß ist wie das Dreieck selber. c cm h Dazu kopiert man das Dreieck und dreht es um 180°. Dann kann man das kopierte und das ursprüngliche Dreieck zu einem Parallelogramm zusammenlegen. Die Fläche eines Dreiecks ist halb so groß, wie die Fläche des Parallelogramms. b cm a cm Es gilt: A = ½ · a · ha A = ½ · b · hb A = ½ · c · hc Städt. RS Kleve Kellen / Klaus Hoffstadt Umfang Trapez Bei einem Trapez sind zwei Seiten parallel. Der Abstand zwischen den parallelen Seiten wird als Höhe h bezeichnet. Der Umfang ist die Summe aller Seitenlängen. Es gilt: u = a + b + c + d c cm h d cm b cm a cm Städt. RS Kleve Kellen / Klaus Hoffstadt Fläche Trapez Es gibt verschiedene Möglichkeiten, ein Trapez in bereits bekannte Flächen umzuformen. Variante 1: Umformen in ein Rechteck c cm Man teilt das Trapez mit der Mittellinie m in zwei Hälften. Da m in der Mitte zwischen c und d liegt, teilt m auch d und b in der Mitte. h x cm Dreht man die durch die Höhen h abgeschnittenen Dreiecke um 180° erhält man ein Rechteck mit der Länge m und der Breite h. m d cm b cm h a cm y cm Folglich gilt: A = m · h da gilt: m = ½ · (a + c) 2 · m = (c + x + y) + (a – x - y)] gilt auch: A = ½ · (a + c) · h Städt. RS Kleve Kellen / Klaus Hoffstadt Fläche Trapez Es gibt verschiedene Möglichkeiten, ein Trapez in bereits bekannte Flächen umzuformen. Variante 2: Zerlegen in ein Dreieck und ein Parallelogramm Man zieht eine Hilfslinie parallel zur Seite b und erhält so ein Dreieck mit der Höhe h und ein Parallelogramm mit der gleichen Höhe h. c cm d cm b cm h Für das Dreieck gilt: A = ½ · (a – c) · h Für das Parallelogramm: A = c · h a-c c a cm Also gilt für das Trapez: A = ½ · (a – c) · h + c · h = ½ · a · h - ½ · c · h + c · h A = ½ · (a + c) · h Städt. RS Kleve Kellen / Klaus Hoffstadt Umfang Raute / Drachen Eine Raute ist zu beiden Diagonalen symmetrisch und alle vier Seiten sind gleich lang. a cm Ein Drachen ist nur zu einer Diagonalen Symmetrisch. Es sind je zwei Seiten gleich lang. a cm Für die Raute gilt: u = 4 · a a cm a cm a cm a cm Für den Drachen gilt: u = 2 · a + 2 · b bzw.: u = 2 · (a + b) b cm b cm Städt. RS Kleve Kellen / Klaus Hoffstadt Fläche Raute / Drachen Es gibt verschiedene Möglichkeiten eine Raute / Drachen in bereits bekannte Flächen umzuformen. Variante 1: Umwandeln in ein Rechteck b cm Die Diagonalen e und f teilen die Raute / den Drachen in vier Dreiecke. Diese kann man zu einem Rechteck zusammen legen. Das Rechteck hat die Länge f und die Breite ½ e. e f a cm Es gilt für die Raute und den Drachen: A = ½ · e · f Städt. RS Kleve Kellen / Klaus Hoffstadt Fläche Raute / Drachen Es gibt verschiedene Möglichkeiten eine Raute / Drachen in bereits bekannte Flächen umzuformen. Variante 2: Zerlegen in zwei Dreiecke Die beiden Diagonalen e und f teilen die Raute / den Drachen in zwei Dreiecke mit den Höhen h1 und h2. Die Summe der beiden Dreiecksflächen entspricht der Fläche der Raute / des Drachen. Es gilt: A = ½ · e · h1 + ½ · e · h2 a cm h1 e f h2 b cm bzw.: A = ½ · e · (h1 + h2) Und damit: A = ½ · e · f Städt. RS Kleve Kellen / Klaus Hoffstadt Umfang zusammengesetzter Flächen Bei zusammengesetzten Flächen ist der Umfang die Summe aller Seitenlängen der zusammengesetzten Fläche. 5 cm 3 cm 5 cm Achtung: Die Seiten der einzelnen Teilflächen können sich teilweise überdecken. Sie zählen nicht mit zum Umfang der zusammengesetzten Fläche. 1 cm 1 cm 2 cm 4 cm 4 cm u = 3 · 5 + 2 · 4 + 3 + 2 + 1 + 1 = 30 u = 30 cm Städt. RS Kleve Kellen / Klaus Hoffstadt Fläche zusammengesetzter Flächen Bei zusammengesetzten Flächen berechnet sich die Fläche aus der Summe bzw. der Differenz der Teilflächen. Im Beispiel berechnet sich die Fläche aus einem Quadrat, einem Dreieck und einem Trapez. 5 cm 3 cm 5 cm 2,5 cm 2 cm 4 cm A = 52 + ½ · 5 · 4 – ½ · (3 + 2) · 2,5 = 28,75 A = 28,75 cm2 Städt. RS Kleve Kellen / Klaus Hoffstadt Umfang / Kreisbogen Kreis Bei der Kreisberechnung reichen die Ideen der Einheitsquadrate und der Umformung in bekannte Flächen nicht mehr aus. Man braucht eine neue, weiter Idee. Diese besteht darin, den gesuchten Wert möglichst genau von oben und unten einzugrenzen. Um den Umfang eines Kreises zu bestimmen, kann man z. B. n-Ecke in und um den Kreis zeichnen. Der Umfang des Kreises liegt dann zwischen dem Umfang des inneren n-Ecks (blaues 8-Eck) und des äußeren n-Ecks (gelbes 8-Eck). Mit zunehmender Anzahl der Ecken wird der Umfang des Kreises immer genauer bestimmt. Es ergibt sich: u = 2 · · r bzw.: u = · d Zur Anschauung im Internet bitte hier klicken! Städt. RS Kleve Kellen / Klaus Hoffstadt Umfang / Kreisbogen Kreis Um die Länge eines Kreisbogens b in Abhängigkeit eines Winkels zu bestimmen, benutzt man den Dreisatz: Man teilt den ganzen Umfang in 360 gleich große Stücke (da ein Kreis bekanntlich in 360° unterteilt ist). Jetzt weiß man, wie groß der Kreisbogen von einem Grad ist. Um den Kreisbogen in Abhängigkeit von zu bestimmen, muss man ihn nur noch mit multiplizieren. Es gilt: b = u · / 360° bzw.: b = (2 · · r · ) / 360° Städt. RS Kleve Kellen / Klaus Hoffstadt Fläche / Kreisausschnitt Kreis Auch bei der Flächenberechnung kann man den genauen Wert beliebig nahe eingrenzen. Man kann einen Viertelkreis z. B. mit Säulen ausfüllen. Die Fläche der dunkleren Säulen ist kleiner als die Fläche des Viertelkreises und die Fläche der helleren Säulen ist größer als die Fläche des Viertelkreis. Mit zunehmender Säulenzahl wird der Wert immer exakter. Für den Kreis gilt: A = · r2 Zur Anschauung im Internet bitte hier klicken! Städt. RS Kleve Kellen / Klaus Hoffstadt Fläche / Kreisausschnitt Kreis Um die Fläche eines Kreisausschnitts A in Abhängigkeit eines Winkels zu bestimmen, benutzt man den Dreisatz: Man teilt die ganzen Kreisfläche in 360 gleich große Stücke (da ein Kreis bekanntlich in 360° unterteilt ist). Jetzt weiß man, wie groß die Kreisfläche von einem Grad ist. Um die Kreisfläche in Abhängigkeit von zu bestimmen, muss man sie nur noch mit multiplizieren. Es gilt: A = ( · r2 · ) / 360° Und weil: b = (2 · · r · ) / 360° gilt auch: A = b · r / 2 Städt. RS Kleve Kellen / Klaus Hoffstadt Formelsammlung Umfang Fläche Quadrat u=4·a A = a2 Rechteck u=2·a+2·b A=a·b Parallelogramm u=2·a+2·b A = a · ha ; A = b · hb Dreieck u=a+b+c A = ½ · a · ha ; A = ½ · b · hb ; A = ½ · c · hc Trapez u=a+b+c+d A = ½ · (a + c) · h ; A = m · h ; m = ½ · (a + c) Städt. RS Kleve Kellen / Klaus Hoffstadt Formelsammlung Umfang Fläche Raute u=4·a A=½·e·f Drachen u=2·a+2·b A=½·e·f Kreis u=2··r;u=·d A = · r2 Kreisausschnitt b = (2 · · r · ) / 360° A = ( · r2 · ) / 360° Städt. RS Kleve Kellen / Klaus Hoffstadt