8b. Bioelektrizitat2
Werbung

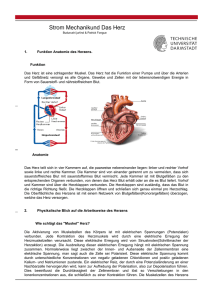
Elektrische und magnetische Phänomene in Lebensvorgängen II. Elektrodynamik Péter Maróti Professor für Biophysik, Universität von Szeged, Ungarn. Lehrbücher: Biophysik für Mediziner (Herausgeber S. Damjanovich, J. Fidy und J. Szöllősi) Medicina, Budapest, 2008. Fercher A.F. Medizinische Physik, Springer, Wien, New York 1992. Haas U. Physik für Pharmazeuten und Mediziner; Wissenschaftliche Verlagsgesellschaft mbH. Suttgart 2002. Jerrentrup A. Physik für Mediziner, Original-Prüfungsfragen mit Kommentar, Schwarze Reihe, 19. Auflage, Thieme Verlag Stuttgart 2009. Maróti P., Laczkó G.: Bevezetés a biofizikába, JATEPress, Szeged 1998 (Ungarisch) P. Maróti, L. Berkes, F. Tölgyesi: Biophysics Problems. A Textbook with Answers. Akadémiai Kiadó, Budapest 1998 (Englisch). Zeitliche Änderungen der elektrischen und magnetischen Erscheinungen ausgelöst durch Bewegung elektrischer Ladungen (Ströme) 0 Elektromagnetische Wellen Versorgungsnetz Gleichstrom Wechselstrom 50 Hz Mikrowellen kHz MHz log (Frequenz, ν) GHz Der elektrische Strom, Grundgesetze Der elektrischer Strom I ist die elektrische Ladungsmenge dQ, die, bezogen auf ein Zeitintervall dt, durch einen Leiter flieβt: dQ I oder Q I dt dt Das Ohmsches Gesetz: die Potentialdifferenz U an den Enden eines Leiter ist proportional zu dem durch den Leiter flieβenden elektrischen Strom I. Der Proportionalitätsfaktor R heiβt elektrischer Widerstand oder Resistanz des Leiters: U RI Der elektrische Widerstand R eines Leiters ist einerseits abhängig von dessen geometrischen Abmessungen, nämlich der Länge l und der Querschnittsfläche A, anderseits vom Leitermaterial. Die Materialabhängigkeit wird als Resistivität (früher: spezifischer Widerstand) ρ bezeichnet: R l A Die elektrische Leistung einer Spannungsquelle ist W U K2 2 P U0 I R I U K I t R U0 heißt eingeprägte Spannung, Urspannung oder elektromotorische Kraft (EMK), UK ist die Klemmenspannung. Die zwei Kirchhoffschen Regeln: 1. Die Knotenregel: An jedem Verzweigungspunkt ist die Summe der zufließenden Ströme gleich der Summe der abfließenden Ströme. Das Gesetz kommt von dem Erhaltungsgesetz der elektrischen Ladungen. Wenn wir dem zufließenden Strom ein positives Vorzeichen, dem abfließenden Strom ein negatives Vorzeichen geben, dann die Summe der Ströme sollte verschwinden an dem Verzweigspunkt. 2. Die Schleifenregel: In einer geschlossenen Stromschleife ist die Summe allerleier Spannungsabfälle entlang der Schleife ist Null, weil die Spannung ist ein Potential(Zustand)funktion. n I i 0 i 0 i 1 n U i 1 Die geschlossene Schleife besteht aus n Knoten (Abschnitten). Vorzeichenregel: die EMK der Spannungsquelle zeigt vom positiven zum negativen Pol und die Spannung an einem Widerstand hat die selbe Richtung wie der durchfließende Strom. n Parallelschaltung von Widerständen: Es folgt aus der Knotenregel, daß sich die reziproken Werte der einzelnen Widerstände zum reziproken Wert des Gesamtwiderstands RG addieren: Reihenschaltung von Widerständen: Es folgt aus der Schleifenregel, daß der Gesamtwiderstand RG einer Reihenschaltung gleich der Summe der Einzelwiderstände Ri ist: 1 RG i 1 1 Ri n RG R i i 1 Knotenregel Parallelschaltung von Widerständen n 1 RG Ii 0 i 1 n i 1 Schleifenregel Reihenschaltung von Widerständen n n U i 1 i 0 RG R i i 1 1 Ri Resistivitäten biologischer Substanzen Resistivität, ρ in Ω·m Stoff Kupfer 1,8·10-8 (guter Leiter) Bernstein > 1016 (Isolierstoff) Urin 0,3 Intrazellulärflüssigkeit 0,6 Plasma 0,63 Extrazellulärflüssigkeit 1 Blut 1,50 Zellmembran 106 bis 109 Herzmuskel 2,5 (longitudinal) 5,6 (transversal) Fettgewebe 25 Nerven grau Nerven weiβ 2,8 Mittelwert aus longitudinalem 6,8 und transversalem Wert. Knochen 166 Körpersubstanzen bei 37 oC und Frequenzen zwischen 20 Hz und 100 kHz. „Longitudinal” und „transversal” bezieht sich auf die Faserrichtung. Die Angaben sind keinesfalls exakte Werte, sondern nur Beispiele. - Es gibt eine erhebliche intraund interindividuelle Streuung. - Die Werte sind oft stark vom Meβverfahren abhängig: 1) Polarisation der Meβelektroden kann die Meβwerte stark verfälschen. 2) Postmortalen Veränderungen bei in-vitro Messungen; z.B. erhebliche Resistivitätsänderungen treten bei Leberzellen bereits nach einer halben Stunde auf. Elektrischer Strom in körperlichen Leitern In Leitern, bei welchen die Querschnittsabmessungen (r) im Vergleich zur Leiterlänge (l) klein sind (r << l), ist die Bewegungsbahn der Ladungen, also der verlauf der Stromlinien, weigehendst klar: sie folgen die geometrischen Form. In körperlichen Stromleitern, das sind Leiter mit Querabmessungen in der Gröβe der Längsabmessungen, ist der verlauf der Stromlinien nicht vorneherein bekannt. Mechanism der Stromleitung in metallischen und elektrolytischen Leitern. Die vom elektrischen Feld erzeugte Driftbewegung der Ladungen wird durch Kollisionen immer wieder unterbrochen. Die Ladungen werden hier vom elektrischen Feld immer wieder von Null aus erneut genau in Richtung des Felds beschleunigt. Die Stromlinien werden daher denselben Verlauf nehmen, wie die elektrischen Feldlinien. Unsere Aufgabe reduziert sich somit auf das Auffinden der elektrischen Feldlinien in körperlichen Leitern. In körperlichen elektrolytischen Leitern folgt der Strom den elektrischen Feldlinien. Spannungsabhängigkeit von Widerständen Unabhängig von der anliegenden Spannung: Ohmischer Widerstand R = 32 kΩ Die Schraffur deutet die Streuung, bedingt durch unterschiedlichen Körperbau und Funktionszustand, an. Menschlicher Körper von Hand zu Hand Körperwiderstand Mittelwert (durchgezogene Kurven) von linker Hand zu rechter Hand in Abhängigkeit von der anliegenden Spannung unmittelbar nach Beginn der Durchströmung (nach Freiberger, 1934). Hautwiderstand Streubereich (schaffiert) Innerer Körperwiderstand Der Hautwiderstand stellt nur innerhalb der ersten Sekunde einen gewissen Schutz dar: Bei 220 V, er sinkt innerhalb von 3 s auf 1/3 oder weniger seines Anfangswerts. Bei 500 V, RHaut<<RInnerer nach 3 s. Bei 5 kV bricht der Hautwiderstand nach 10 ms zusammen. Haut- und innerer Körperwiderstand Hautwiderstand: hängt von mehreren Parametern ab. - Er zeigt große Variabilität inter- und intraindividuell. Verantwortlich sind - die Stärke der Verhornung, - der Feuchtigkeitsgrad, - die Dichte der Schweißdrüsen und - die Durchblutung. - Größe der Berührungsspannung und - Einwirkungsdauer (er nimmt mit zunehmender Spannung als auch mit der Dauer der Einwirkung ab). Innerer Körperwiderstand: im Gegensatz zum Hautwiderstand, er ist – zumindest bei außen angelegten Elektroden – relativ stabil. Die angegebenen Prozentwerte beziehen sich auf einen Gesamtwert des Widerstands von der Hand zum Fuß von 1400 Ω, gemessen an der Leiche eines Erwachsenen (nach Freiberger, 1934) Strom im homogenen Raum (ρ ist Konst.) Metallelektroden im Gewebe Metallelektrode Gewebe Äquipotentialflächen Stromlinien Zwei gut leitende Elektroden in mäβig leitender Umgebung. Das Stromlinienbild ist durch die elektrischen Feldlinien gegeben (durchgezogene Linien). Die Äquipotentialflächen sind gestrichelt. Die Elektrodenoberflächen sind Äquipotentialflächen. Bei überall konstanter Resistivität ρ, haben das elektrische Feld und auch die Äquipotentiallinien bzw. –flächen dieselbe Forme wie im elektrostatischen Fall (siehe z.B. das Feldlinienbild eines elektrischen Dipols). Spezieller Fall: zwei gut leitende ausgedehnte Elektroden in vergleichsweise schlecht leitender Umgebung (z.B. Metallelektroden im Gewebe). Hier kann man die Potentialdifferenzen auf den Elektroden gegenüber jenen der Umgebung vernachlässigen. Dann sind die Elektrodenoberflächen Äquipotentialflächen, und das Problem ist gleich dem elektrostatischen Fall. Strom im inhomogenen Raum. Verlauf der Stromlinien an den Grenzflächen der Bereiche unterschiedlicher Resistivitäten. U I R I E i l l A für bessere Begründung E1|| E2|| Siehe die 3. Maxwell-Gleichung! (i1 1 )|| (i2 2 )|| i1 1 sin 1 i2 2 sin 2 I: Stromstärke, E: Feldstärke, ρ: Resistivität, i = I/A: Stromdichte I1 i1 A' cos 1 i2 A' cos 2 I 2 Bilden wir Quotienten! Ein vollständiger Umlauf einer Ladung entlang der Elektrische Feldstärken gestrichelten Bahn ändert E1 und E2 an der Grenze nicht die potentielle zweier Bereiche mit den Energie dieser Ladung, Resistivitäten ρ1 und ρ2. falls E 1|| = E 2||. Der zwischen zwei Stromlinien der Grenzfläche A’ zuflieβende Strom I1 muβ auch abflieβen I2. Normale auf GF Brechungsgesetz für Stromlinien Die Tangensfuktionen der Winkel, die die Feldlinien mit den Normalen auf die Grenzflächen einschlieβen, verhalten sich umgekehrt wie die Resistivitäten. Grenzfläche zwischen zwei Bereichen mit den Resistivitäten ρ1 und ρ2. Das Brechungsgesetz für elektrische Stromlinien in speziellen Fällen Der einfachste Fall ist wenn die Differenz der Resistivitäten zwischen den Medien sehr groβ ist: ρ2 >> ρ1. Das Brechungsgesetz ergibt für die Tangensfunktionen der Winkel tan α2 << tan α1. Die Stromlinien stehen vom guten Leiter her kommend, im schlechten Leiter praktisch normal auf die Grenzfläche. Entspechend bildet die Oberfläche des guten Leiters etwa eine Äquipotentialfläche. Stromlinien und Äquipotentiallinien (gestrichelt) in inhomogenen Körpern. Ein homogener Leiter mit mäβiger Resistivität ρ1 befindet sich zwischen zwei gut leitenden ebenen Elektroden. Ein zusätzlicher, sehr viel besserer Leiter mit ρ2 << ρ1 konzentriert die Stromlinien auf sich. Ein zusätzlicher, sehr viel schlechterer Leiter mit ρ2 >> ρ1 verdrängt die Stromlinien. Stromwärmeleistung; Erwärmung durch Strom Die Stromwärme-Leistungsdichte ist 2 P I R I i2 V Al A 2 und ist proportional zum Quadrat der Stromdichte i und zur Resistivität ρ. Die Stromwärmeleistung allein sagt aber noch nichts über die Temperaturerhöhung im stromdurchflossenen Körper aus, weil wir auch die Wärmekapazität des Körpers in Betracht nehmen müssen. Die Erwärmung ΔT (Temperaturzunahme) im Zeitintervall Δt ist nicht nur von der erzeugten Wärmeleistung P abhängig, sondern auch von der Wärmekapazität des stromdurchflossenen Bereichs. Da die Wärmekapazität das Produkt aus Massendichte d mal Volumen V mal spezifische Wärmekapazität c ist, es gibt – zumindest bei gleichem Stoff: P t c (d V ) T P t t T i2 V cd cd Die Erwärmung ΔT ist proportional zum Quadrat der Stromdichte i und zur Resistivität ρ des Stoffes. Stromwärmeleistung in quer durchströmten Gliedmaßen Maximale Stromwärmeleistung tritt hier in den Bereichen mit der größten Stromliniendichte auf, also an der linken Eintrittstelle und nahe am Knochen (oben und unten). U2 2 A P U I U R l U2 t A t 2 T U R d V c ldV c 2 t U T l dc 2 t T E dc Resistivität: ρ, Massendichte: d, spezifische Wärmekapazität: c, Δt : Zeitintervall der Erwärmung. Und wirklich, die Temperaturerhöhung ΔT hängt von dem Quadrat der elektrischen Feldstärke E (und deswegen von der Stromliniendichte) ab. Die im Körper erzeugten Stromdichten sind von der Elektrodengröße abhängig Verlauf von Strom- und Äquipotentiallinien (gestrichelt) bei punktförmigen Elektroden an der Oberfläche eines Körpers. Velauf der Stromlinien bei oberfächlich angelegten größeren Plattenelektroden im Körper. (Hoch)spannungsleiter Elektrounfall Geerdete Metallleiter Die Stromwärmeleistung ist nicht die entscheidende Gefahr, sondern die durch Stromfluß im Herzen verursachte Fibrillation des Herzmuskels. Ungefährer Verlauf von Stromlinien vom Stromleiter durch den Körper (auch durch das Herz) zu der Erde. Gefährdungsgrenzen durch Wechselstrom (50 Hz) für den Menschen a: 50% Wahrscheinlichkeit für Herzkammerflimmern b: Sicherheitsgrenze auf der Basis der Gefährdung durch I = 50 mA während 1 s (Brinkman und Schaufer, 1982). Aus Tierversuchen ein Wert von Ieff = 400 mA folgt für Kurzzeitdurchströmungen (< 0,1 s). Der Übergangsbereich zwischen 100 ms und 1 s ist mangels genauer Kenntnis der Determinanten der Flimmerschwellen nicht exakt festlegbar. Leistungsanpassung im Gleichstromkreis Bei welchem Lastwiderstand R wird die einer Spannungsquelle mit dem Innenwiderstand Ri entnehmbare elektrische Leistung maximal? Die Leistung im Lastwiderstand R ist 2 2 U U R PR I 2 R 2 R R R R i 4 Ri i R Der Nenner des letzten Ausdrucks wird minimal (und damit PR maximal), wenn R = Ri Dieses Ergebnis bedeutet übrigens, daß in der Stromquelle (an Ri) dieselbe elektrische Leistung in Wärmeleistung verwandelt wird, wie am Lastwiderstand R. Widerstandsmodell für Gliedmaβen bei Stromfluβ in Längsrichtung In Längsrichtung stromdurchflossene Gliedmaßen können als Parallelschaltung von Haut, Muskelgewebe, Blutgefäβen und Knochen betrachtet werden. U2 2 A P U I U R l U2 A P l Die größte Stromwärmeleistungsdichte entsteht im Gewebe der kleinsten Resistivität und grössten Querschnittfläche (Blut oder Skelettmuskel mit longitudinaler Faserrichtung: ρ = 1,5 Ω·m). Gleichstromresistivität von weichem Gewebe Diese wird wegen des hohen Membranwiderstands hauptsächlich von der Resistivität der interstitiellen Flüssigkeit bestimmt. Die Interstitialspalten von weichem Gewebe sind etwa 1 μm weit. Eine Abschätzung der Resistivität des Gewebes erhält man, wenn man es als Parallelschaltung von Interstitialraum und Zellen auffaßt. Bei einer Zellgröße von 10 μm beträgt die Fläche der Zelle: 10 μm · 10 μm = 100 (μm)2, die Fläche der Interstitialflüssigkeit: 4·10 μm·0,5 μm = 20 (μm)2, und der Flächenanteil der Interstitialflüssigkeit: 1/5. Vereinfachte Geometrie von Interstitialraum (schaffiert) und Zellen. Die Geweberesistivität ist daher etwa 5 mal größer als die Resistivität der interstitiellen Flüssigkeit, d.h. sie beträgt etwa 10 Ω·m. Diese Resistivität wird allerdings je nach Anteil des Interstitialraums in den verschiedenen Gewebearten auch erheblich andere Werte annehmen können. Impedanz-Kardiographie Blutvolumenänderungen bei durchbluteter Organe Laminar strömendes Blut hat kleinere Resistivität als ruhendes Blut Änderungen der elektrischen Impedanz der Brust Herzzeitvolumen KontraktionsSchweregrad bei geschwindigkeit und HerzklappenKontraktilität des insuffizienz Herzmuskels andere Funktionsparameter des Herzens Messungen bei Frequenzen von 10 kHz bis 100 kHz, weil bei diesen Frequenzen - Polarisationserscheinungen an den Elektroden sowie - Hautimpedanz vernachlässigbar sind und - die roten Blutkörperchen im Vergleich zum Plasma noch nichtleitend sind. Die Weglänge des elektrischen Stroms (gestrichelte Linie) durch das Plasma ist kürzer bei strömendem Blut als bei ruhendem Blut. Hochfrequenzchirurgie Die Basis dieses Verfahrens ist die bei Hochfrequenz ausschließlich wirksame Joulesche Stromwärme. Wir schätzen die in dem schaffierten Bereich (Dicke d, Fläche A) auftretende Temperaturerhöhung ΔT im Zeitintervall Δt ab. Die zugeführte Stromwärmeleistung ist 2 2 P I eff R I eff 2 T I eff d t c A2 d d A 2 ieff t c wo c ist die spezifische Wärmekapazität und ρ ist die Resistivität des Gewebes und i ist die Stromdichte I/A. Stromkreis in der (monopolaren) Elektrochirurgie. Die Neutralelektrode wird mittels Gummiband am Körperstamm befestigt. Die aktive Elektrode hat je nach Eingriff unterschiedliche Form. Die Temperaturzunahme wird also am Ort der größten Stromdichte, d.h. direkt an der Elektrode, am größten sein. Da A mit dem Quadrat des Abstands von der Elektrode zunimmt, nimmt ΔT mit der 4. Potenz des Abstands von der Elektrode ab. ΔT hängt ferner von der Verweildauer Δt bzw. der Führungsgeschwindigkeit der aktiven Elektrode ab. Monopolare Operationstechnik ohne Neutralelektrode für kleine Eingriffe Ein besonders kritischer Punkt ist der großflächige Sitz der Neutralelektrode. Löst sie sich, können an den verbleibenden Kontaktstellen hohe Stromdichten und damit verbunden Hautverbrennungen auftreten. Ebenso muß verhindert werden, dass sich der Stromkreis anders als über die Neutralelektrode schließt, weshalb er nicht geerdet werden darf. Das gilt nicht für die monopolare Operationstechnik ohne Neutralelektrode, bei der sich der Stromkreis über die Teilkapazitäten des Körpers zur Erde schließt. Da hier der Verlauf des Stromes unkontrolliert bleibt, ist dieses Verfahren von vornherein auf sehr kleine Leistungen beschränkt, etwa zum Kautern in der Zahnmedizin. Tödlicher kapazitiver Leckstrom bei defektem Schutzleiter Von Herzsonden und Herzkatheter gehen eine besondere Gefährdung aus, weil sie etwaige Fehlströme direkt zum Herz leiten. Es genügen daher schon die in gewöhnlichen Elektrogeräten auftretenden kapazitiven Leckströme, um tödliche Herzströme hervorzurufen. Besonders kritisch ist dies dann, wenn der Patient neben dem Katheter noch mit einem weiteren Elektrogerät, z.B. einem Elektrokardiographen, verbunden ist, dessen Schutzleiter (SL) unterbrochen (UB) ist. Es ist vollkommen unklar, wieviele Unfälle in Intensivstationen durch solche Leckströme bedingt sind („Plötzliches Tod des Herzens”). Der Stromkreis des kapazitiven Leckstroms schließt sich über die Kapazität C1 zwischen der Elektronik des Druckmeßgeräts und dem Druckwandler, die Katheterflüssigkeit, das Herz, die Kapazität C2 zwischen Körper und leitenden Teilen der Liege, sowie dem hierzu gehörigen Schutzleiter SL. Elektromagnetische Wellen im biologischen Gewebe: Eindringtiefe von Mikrowellen in Körpergeweben Die magnetische Permeabilität von Gewebe ist etwa gleich der von Vakuum. Die elektromagnetische Wellen wirken daher auf Gewebe praktisch nur durch die elektrische Feldstärke. Diese Feldstärke erzeugt über Polarisations- und Leitungsströme Joule-sche Stromwärme. Die im Gewebe entstehende Wärme ist sowohl von der elektrischen Feldstärke E als auch von der Dielektrizitätskonstanten ε und der Resistivität ρ des Gewebes abhängig. Bei sehr hohen Frequenzen ist in wasserhaltigen Substanzen wie biologischen Geweben die Orientierungspolarisation der Wassermoleküle der wichtigste dissipative Mechanismus. Die Eindringtiefe t nimmt mit zunehmender Frequenz ν ab (etwa proportional zu 1/√ν). Ferner wird t stark von der Konzentration gelöster Elektrolyte beeinflußt, weil diese der Strahlung durch Leitungsstrom Energie entziehen können. Gebundenes Wasser und größere Moleküle wie Proteine absorbieren stärker bei niedrigeren Frequenzen als freie Wassermoleküle. Eindringtiefe (t): Weglänge, bei der die Strahlungsintensität auf den Bruchteil 1/e2 abgesunken ist. Ab etwa 1 GHz beschränkt sich die Erwärmung zunehmend auf die Oberfläche. Magnetfeldtherapie einer Knochenfraktur: über Wärme hinausgehende Wirkung. Bioelektrischer Regelkreis, der die Knochenbildung steuern kann: 1) piezoelektrischer Effekt des Knochenkollagens und 2) elektrische Gewebereizung Äußere Spulen die von Wechselstrom durchgeflossen sind. Bei der operativen Frakturbehandlung wird eine Induktionsspule mittels zweier Elektroden an den Osteosyntheseschrauben befestigt. Das von der äußeren Spule erzeugte magnetische Wechselfeld B induziert in der an die Bruchstelle implantierten Spule eine Wechselspannung, die einen entsprechenden Strom und Wärme zur Folge hat. Prinzip der Defibrillation Kammerflimmern, egal welcher Ursache, bedeutet Kreislaufstillstand. Dauert dieser Zustand länger als 3 bis 4 Minuten, wird das Gehirn irreversibel geschädigt. Durch einen starken Elektroschock am Herzen, der alle Muskelfasern zur selben Zeit kontrahieren läßt, kann sich die Herzmuskeltätigkeit wieder synchronisieren . Direkt am Herzen, also bei (operativ) geöffnetem Thorax, sind dazu Spannungen um 1000 V und Ströme um 20 A für die Dauer von etwa 5 ms erforderlich. Der Kondensator C wird auf die erforderliche Spannung aufgeladen und liefert nach Umlegen des Schalters den Defibrillationsstromstoβ. Die Elektroden werden an gegenüberliegenden Enden der Herzachse angelegt. RC-Kreis zum Modellieren der Vorgänge, die sich in der Membran nahe dem Ruhepotential abspielen. Aktionsstrom der Reizprozesse Membran Transversaler Membranwiderstand Membrankapazität Aufladen eines parallel geschalteten RC-Kreises Strom t I R I 1 e RC IC I e I IR IC (U R ) R I R IC I·RC Ladung t RC Nach den Kirchhoffschen Gesetzen: t Q I RC 1 e RC dQ dt Drei Unbekannten (IR, IC und Q), drei Gleichungen: Q dQ RC dt dQ dt Q I RC t Q(t ) I RC 1 e RC I Spannung t U R U C IR 1 e RC Q ( U C ) C Zum Erreichen der Depolarisationsschwelle UDep ausgehend von dem Ruhepotential URuhe, ist entweder ein niedriger aber langdauernder Stromimpuls, oder ein kurzer aber starker Impuls erforderlich. Bis zum Erreichen der Depolarisationsschwelle ändert sich das Membranpotential wie die Exponentialkurve eines parallel geschalteten RC-Kreises (gemeinsamer Abschnitt der schwarzen und roten Kurven). Reizstromgesetz (nach Hoorweg und Weiss) Eine wichtige Methode der Reizstromdiagnostik ist die Bestimmung 1) der Rheobase (Schwellstromstärke Imin zur Auslösung einer Muskelzuckung) und 2) der Chronaxie (erforderliche Reizzeit T bei zweifacher Schwellstromstärke) der elektrischen Erregbarkeit. Ein Maß für die Schädigung eines Muskels. Um die Schwelle der Zelle zu erreichen, ist eine Potentialzunahme UDep – URuhe erforderlich, was bei einer Reizzeit T durch einen Reizstrom I erreicht ist T U Dep U Ruhe IR 1 e RC Der Minimalwert von I , die sogenannte Rheobase Imin ist Nach Einsetzen den Wert der Rheobase: I I min I min T RC 1 e oder U Dep U Ruhe R I T R C ln I I min Dies ist die Reizschwellengleichung. Sie gibt qualitativ die Abhängigkeit des Reizstroms von der Reizzeit wieder. Bemerkt sei, dass die bei klinischen Chronaxie-Bestimmungen benutzten konstanten Stromstärken in einem festen Verhältnis zu Imin stehen, welches durch die Quotientenbildung Imin/I herausfällt. Herzschrittmacher Wenn Medikamente nicht mehr zur Behandlung einer Herzrhytmusstörung ausreichen, und wenn die verschiedenen natürlichen Taktgeber des Herzens versagen, dann wird zum Anlegen eines Herzschrittmachers geraten. Er gibt elektrische Spannungsimpulse in der Größe zwischen 2,5 V und 5 V über Elektroden an den Herzmuskel und lösen dadurch Aktionspotentiale aus. Im prinzip besteht ein Schrittmacher aus einem Kondensator, der periodisch auf die Stimulationsspannung aufgeladen wird und sich über den Herzmuskel entlädt. Die Reizschwellengleichung kann man anstatt für Ströme auch für Spannungen schreiben: U U min 1 e T / Tc Die Chronaxiewerte für Stimulationselektroden mit etwa 10 mm2 Kontaktfläche liegen in der Größenordnung von Umin = 1 V und Tc = 0,45 ms. Sicherheit des Herzschrittmachers Bei Schrittmacher wird meist eine 100% Sicherheit gewählt, d.h. man verdoppelt die vom Schrittmacher bei der gewählten Stimulationszeit T mindestens erforderliche Reizspannung. Nehmen wir an, es steht eine Schrittmacher-Ausgangsspannung von 5 V zur Verfügung. Dann muß eine Stimulationszeit T gewählt werden, bei welcher bereits U = 2,5 V eine Reize auslöst, d.h. U T Tc ln U U min Das Magnetfeld, das von vielen Kopfhörern ausgeht, kann Herzschrittmacher aus dem Takt bringen. Umin = 1 V und Tc = 0,45 ms. U (V) T (ms) 2,5 0,23 5,0 0,10 Also, Sicherheit halber, man muß lieber T = 0,3 ms Anregungszeit einstellen um der Schrittmacher auch bei U = 2,5 V Spannung arbeiten zu können. Iontophorese Hier wird die elektrolytische Elektrizitätsleitung benutzt, um Medikamente mittels Gleichstroms durch die unverletzte Haut lokal in den Körper zu transportieren. Als Medikamente sind nur solche geeignet, die bei pH 4,5 bis 5,5 als Ionen vorliegen. Basen können über die Anode, Säuren über die Kathode appliziert werden, z.B. von der Anode her Adrenalin, Bienengift, Histamin, Procain u.a. Leduc-scher Kaninchenversuch mit positiv geladenem Strychnin. Die rot gezeichneten Elektroden enthalten Strychnin in der Unterlage. Das linke Kaninchen stirbt an Strychninvergiftung, das rechte bleibt unversehrt. Dazu wird die Elektrodenunterlage mit einer Lösung oder einem entsprechenden Gelpräparat getränkt. Da die Wanderungsgeschwindigkeit dieser relativ großen Moleküle sehr klein ist, bleibt ihre Eindringtiefe begrenzt. Sie werden in der Subkutis vom Blut- und Lymphstrom erfaßt und abtransportiert. Jedenfalls ist die Resorption deutlich besser als bei bloßer Einreibung des Medikaments. Da die Iontophorese elektronisch steuerbar ist, kann damit ein medikamentöses Regelsystem verwirklicht werden. IontophoresePflaster mit integrierter Elektronik und Batterie können tagesrhytmische oder symtombedingte Dosierungsschemata realisieren. Hall-Effekt Gleichgewicht ist zwischen der Lorentzkraft: FL Q v B und der Kraft des elektrischen Felds: FE Q E Qv BQ E Das Hall-Feld ist: E = v·B Die Hall-Spannung ist: oder A: Leiterquerschnittsfläche, n: Ladungsträgerdichte, e: elektrische Elementarladung, v: Ladungsträgergeschwindigkeit, B: magnetische Induktion, E: elektrische Feldstärke, Q: Ladung des Teilchens und d: Abstand zwischen den zwei HallElektroden. UH E d v B d I Bd UH ne A Die Bedeutung der Hall-Spannung ist die Bestimmung - der Magnetfeld Induktion, - die Natur (+ oder -) der Ladungsträger (aus der Polung der Hall-Spannung) - Ladungsträgerdichte des betreffenden Leiters. Elektromagnetische Blutflußmessung Das Blut bewegt sich im Magnetfeld. Die operativ freigelegte Blutgefäße werden zwischen die Pole eines Elektromagneten gebracht, dass das Blut senkrecht zum Magnetfeld B strömt. Dann mißt man an der Gefäβwand mit zwei Elektroden die HallSpannung: UH v B d aus der die Geschwindigkeit v berechnet werden kann. Um Polarisationseffekte zu vermeiden, wird mit einem magnetischen Wechselfeld von etwa 1 MHz gearbeitet. Hall-Spannungen treten auch dann auf, wenn die Blutgefäβe nicht freigelegt sind und der Mensch sich in einem starken Magnetfeld aufhält. Bis zu Feldstärken von B = 2 T treten nach den gegenwärtigen Einsichten hierbei keinerlei schädliche Störungen der physiologischen Vorgänge im Körper auf. Hall-Spannungen treten darüber hinaus auch an anderen bewegten Leitern im Körper auf, beispielweise am Herzmuskel. Hausaufgaben 1. Berechnen Sie den elektrischen Widerstand eines Muskelgewebestücks von 1 mm Durchmesser und 1 cm Länge. 2. Wie groß ist die Stromstärke einer 100 W Haushaltsglühlampe? 3. Wie groß ist die Kapazität eines Defibrillationskondenzators von 3 kV Spannung, wenn die Defibrillationsenergie 360 J sein muß? 4. Berechnen Sie den inneren Körperstroms von der rechten Hand zum Gesäβ bei einer Spannung von 220 V nach Zusammenbrechen des Hautwiderstands nach Angaben von Freiberger (1934). 5. Wie groß ist der effektive kapazitive Strom, der über Gehäuse und Nulleiter fließt bei Haushaltsgeräte? Typische Kapazität für Haushaltsgeräte liegt bei C = 10 nF. 6. Für die elektrolytische Wirkung von Strom ist die transportierte elektrische Ladung Q ausschlaggebend. Wie groß ist Q für eine Wechselstromperiode in dem elektrischen Nahversorgungsnetz (Ueff = 220 V, ν = 50 Hz)? Hausaufgaben 7. Wie groß ist die Kapazität eines Kondensators, der sich über einen 500 kΩ Widerstand mit einer Zeitkonstanten von 10 s entlädt? 8. In einem Zimmer sind (parallel geschaltet) eine Lampe von 100 W und ein Heizlüfter von 1 kW in Betrieb. Die Netzspannung beträgt 230 V. Wie groß ist die Gesamtstromstärke? 9. Eine mobile medizinische Notfallsituation mit einer Leistungsaufnahme von 2 kW wird durch eine Batterie von Bleiakkumulatoren mit 220 Ah „Kapazität” (verfügbarer Ladungsmenge) und 100 V Betriebsspannung versorgt. Die Versorgung würde zusammenbrechen, wenn die „Kapazität” auf 10% gesunken ist. Bis zu diesem Zeitpunkt bleibt die Spannung annähernd 100 V. Etwa wie lange kann die Station betrieben werden, wenn die Akkumulatoren zunächst voll aufgeladen sind und nicht ausgetauscht werden können? 10. Ein Elektroskalpell (zum „Schneiden” mit elektrischem Wechselstrom in der Chirurgie) wird als „monopolare” Elektrode verwendet. Die Gegenelektrode („Neutralelektrode”) am Rücken des Patienten hat eine Kontaktfläche von atwa 500 cm2. Der Strom zwischen den Elektroden hat eine Frequenz von etwa 500 kHz und eine Stromstärke von etwa 1 A. Die Ladungsträger treten senkrecht durch die Kontaktfläche. Wie groß ist die Stromdichte an der Gegenelektrode? Hausaufgaben 11. Welcher Strom fließt bei vollständigem Kurzschluß durch einen Akkumulator von 2 V und 0,05 Ω Innenwiderstand? 12. Wickelt man von einer Spule 10 m Draht ab, so erhöht sich bei derselben Spannung der Strom von 1,52 A auf 1,54 A. Wieviel Meter Draht enthält die volle Spule? 13. Die Klemmenspannung einer Baterie hat bei einem äußeren Widerstand 17 Ω den Betrag 4,4 V und bei 9 Ω den Betrag 4,3 V. Wie groß sind die elektromotorische Kraft (EMK) und der innere Widerstand der Batterie? 14. Von einem geraden Stück Draht der Länge l wird ein Stück x abgeschnitten und der Länge nach mit dem Rest verlötet. Wie lang mußdas Stück x sein, wenn der Widerstand nunmehr den halben Wert haben soll? 15. In welchem Verhältnis stehen zwei Widerstände zueinander, die bei gleicher Spannung in Parallelschaltung die 6-fache Leistung wie in Reihenschaltung verbrauchen?