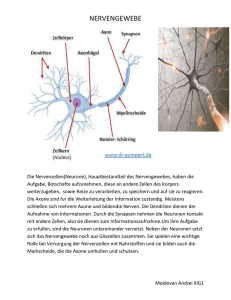
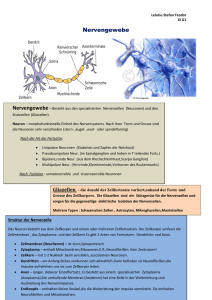
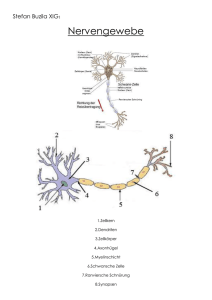
Neuronale Netze
Werbung

Künstliche Neuronale Netze Stefan Hartmann Forschungszentrum caesar Gehirn Computer Anz. Recheneinheiten 1011 109 Art Recheneinheiten Neuronen Transistoren Art der Berechnung Massiv parallel i.d.R. seriell Datenspeicherung assoziativ 10-3s adressbasiert 10-9s Theoretische Schaltvorgänge 1013s-1 1018s-1 Tatsächliche Schaltvorgänge 1012s-1 1010s-1 Schaltzeit Warum Neuronale Netze? • Neuronale Netze sind eine von der Natur inspirierte Methode, Computer lernfähig zu machen. • Sie können Vorgänge im menschlichen Gehirn simulieren. • Anwendungen Neuronaler Netze (u.a.): - Mustererkennung, z.B. Sprach- und Schrifterkennung - Optimierung von Vorgängen, etwa in der Industrie - Künstliche Intelligenz Ein einfaches Anwendungsbeispiel 1. 2. Das folgende Neuronale Netz soll Ziffern von 0 bis 9 erkennen. Dafür wird zunächst das Eingabefeld in 8x15 Elemente aufgeteilt: Die geschriebene Ziffer wird in eine Folge von Nullen und Einsen umgewandelt, wobei 0 für leere und 1 für übermalte Rasterpunkte steht: 3. Nach erfolgreichem Training schafft es das abgebildete Neuronale Netz, geschriebene Ziffern zu erkennen und diese als Output y auszugeben. Vorteile gegenüber klassischen Rechenmethoden: • Lernfähigkeit • Generalisierungsfähigkeit • Fehlertoleranz (etwa bei verrauschten Daten) • Parallelität Geschichtlicher Überblick Anfänge • • Renaissance Ernüchterung • 1943: Warren McCulloch und Walter Pitts beschreiben und definieren eine Art erster neuronaler Netzwerke. 1949: Formulierung der Hebb‘schen Lernregel (nach Donald O.Hebb) 1957-1958: Entwicklung des Perzeptrons durch Frank Rosenblatt • 1969: Marvin Minsky und Seymour Papert untersuchen das Perzeptron mathematisch und zeigen dessen Grenzen, etwa beim XOR-Problem, auf. • 1982: Beschreibung der ersten selbstorganisierenden Netze (nach biologischem Vorbild) durch Teuvo Kohonen und Publikation eines richtungweisenden Artikels von John Hopfield, indem die ersten Hopfield-Netze (nach physikalischen Vorbild) beschrieben werden 1986: Das Lernverfahren Backpropagation für mehrschichtige Perzeptrons wird entwickelt. • Donald O.Hebb John Hopfield Die Struktur Neuronaler Netze Ein Neuronales Netz kann mathematisch als gerichteter Graph aufgefasst werden, das bedeutet: • Es besteht aus einer Menge von Eckpunkten X, • die durch eine Menge von Kanten („Pfeile“) H verbunden sind, die je zwei Eckpunkte gerichtet verbinden. Input Output Die sog. Knoten des Graphen (Eckpunkte, in denen mind. ein Pfeil aufhört und ein Pfeil anfängt) bilden die Grundlage für die Neuronen. Netztopologien FeedForward-Netze: Gerichtete Verbindungen nur von niedrigen zu höheren Schichten FeedBack-Netze (rekurrente Netze): Verbindungen zwischen allen Schichten möglich FB-Netz mit Lateralverbindungen FF-Netz erster Ordnung FF-Netz zweiter Ordnung FB-Netz mit direkter Rückkopplung Das Neuron Biologisches Neuron Dendriten empfangen Reize, die als Potentiale aufsummiert werden. Überschreitet diese Summe ein Schwellenpotential, feuert das Neuron… ...und leitet über das Axon ein Aktionspotential weiter, das über Synapsen an benachbarte Zellen übertragen wird. Künstliches Neuron Die gewichteten Ausgaben anderer Neuronen werden empfangen (Input) und (in der Regel) aufsummiert. Es wird unter Berücksichtigung eines Schwellenwertes der Aktivierungszustand berechnet,… ...von dem wiederum die Ausgabe (Output) des Neurons abhängt. Die technische Realisierung des Neurons • i: Index des Neurons • e1,e2,...ek: Eingabewerte • • • • (Inputs) wi,j: Faktor, mit dem die Verbindung von Neuron i zu Neuron j gewichtet wird, wi=(w1i,…,wki) neti: Nettoinput des i-ten Neurons ai: Aktivierung des i-ten Neurons oi: Ausgabewert (Output) des i-ten Neurons, meist identisch zur Aktivierung Die Inputfunktion Die Input- oder Propagierungsfunktion berechnet aus dem Eingabevektor e e1 ,..., ek und dem Gewichtsvektor wi w1,i ,..., wk ,i den Nettoinput des i-ten Neurons. Es gibt folgende Inputfunktionen: • Summe: k neti f in wi , e w j ,i e j j 1 w j ,i e j • Maximalwert: neti fin wi , e max j • Produkt: • Minimalwert: neti fin wi , e min w j ,i e j j Die Aktivierungsfunktion Mit der Aktivierungsfunktion (auch: Transferfunktion) wird aus dem Nettoinput der Aktivierungszustand des Neurons berechnet. Folgende Aktivierungsfunktionen sind üblich: • Lineare Aktivierungsfunktion: ai f act neti ci neti Schwellenwert , häufig 0 1, falls neti i 0, sonst • Binäre Schwellenwertfunktion: ai f act neti • Fermi-Funktion (logistische Funktion): ai f act neti 1 1 e neti T e neti e neti 1 tanh neti • Tangens hyperbolicus: ai f act neti neti neti 2 e e Lineare Aktivierungsfunktion Schwellenwertfunktion Fermi-Funktion Tangens hyperbolicus Die Outputfunktion • Die Outputfunktion berechnet aus der Aktivierung ai den Wert, der als Ausgabe an die nächste Neuronenschicht weitergegeben wird. • In den meisten Fällen ist die Outputfunktion die Identität, d.h. oi=ai . • Für binäre Ausgaben wird manchmal auch eine Schwellenwertfunktion verwendet: 1, falls ai i , oi f out ai 0, sonst . Aufgabe 1 Neuron Aktivierungsfunktion des Neurons Gewichtsvektor 1 Linear; c=1 (1) 2 3 4 (1) SchwellenwertFunktion; 0 (1,-2) (-1,0) 5 (3,2) 6 (0,2) 7 Linear; c=1 (0,2,-3,1) 8 (1,-2,3,8) 9 (0,2,3,-4) Eingabewerte: x1=2; x2=1 Berechne den Output des gegebenen Neuronalen Netzes. (Die Nummerierung der Verbindungen gibt an, welche Komponente des Gewichtsvektors sie darstellen.) Welche Neuronen können parallel arbeiten, welche müssen aufeinander warten? Frage Wie könnte eurer Meinung nach ein Neuronales Netz trainiert werden? Welche Bestandteile des Netzes könnten im Lernprozess verändert werden? Lernmodi • In einer Trainingsphase werden Trainingsvektoren p p1 ,..., pk aus einer Trainingsmenge P vorgegeben, die das Netz lernt, indem es Gewichte und evtl. Schwellenwerte verändert. • In der Ausführungsphase wird das gelernte Wissen zur Lösung unbekannter Probleme eingesetzt. Frage Worauf muss man bei der Auswahl geeigneter Trainingsdaten achten? Das Panzerproblem der DARPA (Behörde des Verteidigungsministeriums der USA) Diese Fehler können bei einer ungeeigneten Trainingsmenge auftreten: Zu viele Trainingsbeispiele: Zu wenig Trainingsbeispiele: das Netz hat „auswendig gelernt“ keine richtige Klassifikation Die Trainingsmenge bei überwachtem Lernen Bei überwachtem Lernen wird die Trainingsmenge häufig aufgeteilt in • eine Trainingsmenge, mit der wirklich trainiert wird • und eine Testmenge, mit der die Lernfortschritte getestet werden. Erst wenn das Netz sowohl auf den Trainingswie auch auf den Testdaten gute Werte liefert, wird das Training beendet. Lernstrategien Überwachtes Lernen (supervised learning) Unüberwachtes Lernen (unsupervised learning) • Dem Netz werden beim Training Eingabe- und gewünschte Ausgabevektoren vorgegeben. • Dem Netz werden beim Training nur Eingabevektoren vorgegeben. • Das Netz lernt, bis dahin unbekannten Eingabevektoren plausible Ausgabevektoren zuzuordnen (Generalisierung). • Das Netz erkennt selbstständig Klassen in der Datenmenge und passt seine Parameter an diese an (Autoadaption). Die Hebb‘sche Lernregel „Wenn ein Axon der Zelle A [...] Zelle B erregt und wiederholt und dauerhaft zur Erzeugung von Aktionspotentialen in Zelle B beiträgt, so resultiert dies in Wachstumsprozessen oder metabolischen Veränderungen in einer oder in beiden Zellen, die bewirken, dass die Effizienz von Zelle A in Bezug auf die Erzeugung eines Aktionspotenzials in B größer wird.“ (Donald Olding Hebb, Psychologe, 1949) Das bedeutet: Je häufiger im Gehirn zwei Neuronen gleichzeitig aktiv sind, desto stärker wird die Verbindung (Synapse) zwischen ihnen. Die Hebb‘sche Lernregel 2 Bei künstlichen Neuronalen Netzen wird dieses Phänomen mathematisch mit folgender Formel simuliert: wi , j oi a j Gewichtsänderung von Neuron i nach j Lernrate Ein zweischichtiges Neuronales FeedForward-Netz, das nach der Hebb‘schen Lernregel arbeitet, wird auch linearer Assoziierer genannt. Satz Der lineare Assoziierer arbeitet auf den Trainingsdaten perfekt, falls die Eingabeneuronen ein orthonormales Vektorsystem bilden, d.h. falls sie die Länge 1 besitzen und senkrecht aufeinander stehen. Aufgabe 2 • Das Programm „LINASSOZ.C“ ist ein einfacher linearer Assoziierer mit zwei Neuronenschichten. Öffne das Programm und versuche, es nachzuvollziehen. • Die Unterprogramme lernen() und ausführen() fehlen noch. Ergänze sie so, dass das programmierte Neuronale Netz die Hebb‘sche Lernregel anwendet und beim Ausführen die korrekten Ausgabevektoren liefert! • Benutze danach das fertige Programm: Trainiere das Netz für n=2 und m=1 mit den folgenden Daten und lasse dir das Netz anzeigen. x (1) (0,0); y (1) 0 x ( 2 ) (1,0); y ( 2 ) 1 x ( 3) (0,1); y ( 3) 1 • Lasse das Netz mit denselben Daten im Ausführmodus arbeiten. • Setze nun das Training mit folgender Assoziation fort: 1 1 x ( 4 ) , ; y ( 4 ) 1 2 2 • Welche Ausgaben liefert das Netz im Ausführmodus zu den vier Trainingsvektoren? Warum? Die Fehlerfunktion Der spezifische Fehler für ein Trainingsbeispiel p ist wie folgt definiert: 1 2 Errp o o 2 O Mit werden Outputneuronen bezeichnet; mit O die Menge derselben Summiert man den spezifischen Fehler aller Trainingsbeispiele auf, ergibt sich der Gesamtfehler: Err Errp pP Die Delta-Regel Die Delta-Regel vergleicht den tatsächlichen Output eines Neurons und den Solloutput. Ziel ist es, durch mehrfache Anwendung die Netzausgabe in Richtung der erwarteten Ausgabe zu verschieben. wi , j oi o j o j Solloutput Fragen Warum kann die Delta-Regel nur auf FeedForward-Netze mit maximal 2 Neuronenschichten angewendet werden? Wie verändert sich das Gewicht in den folgenden Fällen? 1. Der beobachtete Output ist zu niedrig. 2. Der beobachtete Output ist zu hoch. 3. Der beobachtete Output ist genau richtig. wi , j oi o j o j Das (Singlelayer-)Perzeptron Ein Perzeptron ist ein zweischichtiges, überwacht lernendes Neuronales FeedForward-Netz. Der Aufbau des Perzeptrons Ein Perzeptron hat folgende Bestandteile: Retina • Die Retina- eine Neuronenschicht, die nur der Datenaufnahme dient und statische Gewichte zur nächsten Schicht hat, • Die Eingabeschicht- bestehend aus Eingabeneuronen die ihren Input als Ausgabe weitergeben (sogenannten Identitätsneuronen) • Im Lernprozess veränderbare Gewichte zwischen Ein- und Ausgabeschicht • Die Ausgabeschicht- bestehend aus sog. Informationsverarbeitenden Neuronen (d.h. die Aktivierungsfunktion ist nicht die Identität) Eingabeschicht Trainierbare Gewichte Ausgabeschicht Wie lernt ein Perzeptron? • Die Aktivierungsfunktion des Perzeptrons ist die binäre Schwellwertfunktion: 1, falls wi , j e j j oi ai 0, sonst Schwellenwert • Während des Lernprozesses werden alle Trainingsvektoren p p1 ,..., pk an das Netz angelegt, und die Ausgaben mit den erwartetem Solloutput verglichen • Die Gewichte werden nach der Delta-Regel modifiziert. • Bewiesen ist das „Perzeptron-Konvergenz-Theorem“: Der Algorithmus konvergiert – das Perzeptron kann in endlicher Zeit all das lernen, was es überhaupt theoretisch abbilden kann. Aufgabe 3 • Das Programm „PERCEPT1.C“ ist ein Perzeptron. Öffne das Programm und versuche, es nachzuvollziehen. • Die Unterprogramme lernen() und ausführen() sind unvollständig. Ergänze sie so, dass das Programm läuft (siehe Kommentare im Listing). • Benutze das fertige Programm: Trainiere das Netz für n=2 und m=1 mit den folgenden Daten und lasse dir das Netz anzeigen. x (1) (0,0); y (1) 0 x ( 2 ) (1,0); y ( 2 ) 1 x ( 3) (0,1); y ( 3) 1 • Teste das Netz im Ausführmodus. • Trainiere das Netz weitere Male mit den gleichen Daten, ohne die Gewichte zu ändern und teste es danach im Ausführmodus. Was fällt auf? Das XOR-Problem • XOR steht für „exclusive or“ und bedeutet soviel wie „entweder oder“ • Ein Perzeptron kann diese Funktion nicht simulieren! 0 entspricht „falsch“, 1 entspricht „wahr“ e1 e2 o 0 0 0 1 0 1 0 1 1 1 1 0 Beweis Angenommen, es gibt ein Perzeptron mit den Gewichten w1 und w2, welches die XOR-Funktion simuliert. Dann müsste gelten: e1 0, e2 0 w1e1 w2e2 0 e1 0, e2 1 w1e1 w2e2 w2 e1 1, e2 0 w1e1 w2e2 w1 e1 1, e2 1 w1e1 w2e2 w1 w2 Widerspruch! Lineare Separierbarkeit Bei dem Perzeptron (hier Eingabeneuronen i und j, Ausgabeneuron ) wird von einem Ausgabeneuron der Wert 1 ausgegeben, wenn gilt: net ei wi , e j w j , 1 ei ( e j w j , ) wi , (Für positives wi, Lineare Separierbarkeit 2 ei 1 0 0 1 ej Ein Single-Layer-Perzeptron kann nur linear separierbare Mengen klassifizieren. (bei n Eingabeneuronen nur Mengen, die durch eine (n-1)-dimensionale Hyperebene trennbar sind) Aufgabe 4 Wie sehen die beiden Perzeptrons aus, die die AND-Funktion (das logische „Und“) bzw. die OR-Funktion (das logische „Oder“) simulieren können? Mehrschichtige Perzeptrons • Die sogenannten Multilayer-Perzeptrons (MLP) mit einer oder mehreren verdeckten Schichten können das XOR-Problem lösen. • Allerdings können MLPs nicht mehr mit der einfachen Delta-Regel trainiert werden! Backpropagation (BP) • Der BackpropagationAlgorithmus arbeitet mit der erweiterten DeltaRegel • Zuerst wird die hinterste Gewichtsschicht verändert, dann arbeitet sich BP weiter nach vorn Die erweiterte Delta-Regel • Die erweiterte Delta-Regel ist auf drei- oder mehrschichtige Neuronale FeedForward-Netze anwendbar: wi , j oi j falls n j Ausgabeneu ron ist , f 'act net j o j o j , j f ' net w , sonst . k j ,k j act kK Gradientenabstieg Der Gradient stellt eine Verallgemeinerung der Ableitung für Funktionen mehrerer Variablen dar. Er ist ein Vektor, in dessen Komponenten die partiellen Ableitungen stehen, der in die Richtung des steilsten Anstieges zeigt und dessen Länge ein Maß für die Steilheit (Steigung) ist. Die Backpropagation ist ein Gradientenabstiegsverfahren, das entgegen der Richtung des Gradienten nach einem Minimum in der Fehlerfunktion sucht. Der BP-Algorithmus Die folgenden Schritte werden für jedes Trainingsmuster durchgeführt. Das Ganze wird wiederholt, bis der Gesamtfehler klein genug oder die maximal verfügbare Zeit überschritten ist: 1. 2. 3. Ein Trainingsmuster wird angelegt und der Output berechnet. Der Fehler für dieses Muster wird berechnet. Der Fehler wird von der Ausgabe- zur Eingabeschicht zurück propagiert und die Gewichte werden, beginnend mit der hintersten Schicht, nach der erweiterten Delta-Regel angepasst. Aufgabe 5 Nun geht es darum, ein Multilayer-Perzeptron mit einer versteckten Schicht zu trainieren. Öffne hierzu das Programm „BACKPROP1.C“. 1. Versuche, die Struktur nachzuvollziehen. 2. Trainiere das Netz für n=2, q=2, m=1, t=4, beta=1, lambda=0.5, s_max=1 und epsilon=0.0001 auf dem XORProblem. Lasse es dir danach anzeigen und führe es auf den XOR-Eingabevektoren aus. Beurteile die Resultate. 3. Wiederhole die obigen Schritte, diesmal aber mit s_max=10000. Was fällt auf? Wie konnte das passieren??? Probleme bei der Backpropagation Mögliche Fehler bei einem Gradientenabstieg: a) Finden schlechter Minima; b) Quasi-Stillstand bei kleinem Gradienten; c) Oszillation in Schluchten; d) Verlassen guter Minima Lösungsansatz 1: Der Momentum-Term wi , j t o j i wi , j t 1 0 1 Auf Plateaus wird beschleunigt, da der Gradient dort ständig das gleiche Vorzeichen hat. Auf zerklüfteten Flächen bremst der Momentum-Term den Gradientenabstieg, da sich das Vorzeichen der Gewichtsänderung ständig ändert. Lösungsansatz 2: Weight Decay Bei dieser von der Natur inspirierten Erweiterung des Fehlers werden zu große Gewichte bestraft: 1 ErrW D Err 2 w2 wW 0 0.02 Das Netz hält die Gewichte klein, sodass das Lernen kontrollierter wird und die Fehlerfunktion weniger stark schwankt. Anwendungsbeispiel: Farbkonstanz Als Farbkonstanz wird das Phänomen bezeichnet, dass die Farbe eines Objektes bei unterschiedlicher Beleuchtung immer gleich wahrgenommen wird, auch wenn die Wellenlänge des reflektierten Lichtes variiert. Diese Erdbeeren werden von uns z.B. als rot statt eigentlich orange oder violett wahrgenommen. Erklärungsansatz • Das menschliche Gehirn bekommt als Eingabe die Wellenlängen des vom Objekt reflektierten Lichts und des Hintergrundlichts. • Vernetzte Neuronen (im visuellen Areal V4 des Kortex) verarbeiten diese Informationen. • Als Ausgabe liefern die Neuronen dann die subjektiv wahrgenommene Farbe, die sich von der tatsächlichen unterscheiden kann. Im Jahre 2004 wurde dieser Prozess im Gehirn mit Hilfe eines Neuronalen Netzes simuliert. Netzaufbau Input-Schicht: Sechs Eingabeneuronen, die in zwei Farbkanäle zu je drei Zapfen aufgeteilt sind • R-Zapfen für langwelliges (rotes) Licht • G-Zapfen für mittelwelliges (grünes) Licht • B-Zapfen für kurzwelliges (blaues) Licht Erste Hidden-Schicht: Statische Gewichte zur Input-Schicht, pro Farbkanal drei Gegenfarbenzellen • R-G: Aktivierung durch rotes, Hemmung durch grünes Licht • B-G: Aktivierung durch gelbes (Wellenlänge zwischen rot und grün), Hemmung durch blaues Licht • S-W: Aktivierung durch weißes Licht (Mischung von rot und grün) Zweite Hidden-Schicht: Trainierbare Gewichte zur vorigen Schicht, Zusammenführung der Farbkanäle Output-Schicht: Ebenfalls trainierbare Gewichte, Ausgabe soll die subjektiv empfundene Wellenlänge sein Der obere Farbkanal verarbeitet die Wellenlänge der Hintergrundfarbe, der untere die der Objektfarbe. Training • Das Netz wurde auf Trainingsbeispielen mit 40 verschiedenen Objektfarben (Hintergrundfarbe konstant) und 9 Beleuchtungsarten trainiert. • Die erwarteten Outputwerte waren vorgegeben, es wurde nach der Backpropagation-Lernregel gelernt. Ergebnisse 1. Das trainierte Netz zeigte auch bei unbekannten Beispielen Farbkonstanz. 2. Die Lernleistung war bei hoher Farbsättigung besser. 3. Es gab eine große Ähnlichkeit zu der Farbwahrnehmung im menschlichen Gehirn. Neuronale Netze sind ein vielversprechender Ansatz, der z.B. auch bei der Entwicklung von Roboteraugen genutzt werden kann. ABER: Das menschliche Gehirn lernt, anders als das hier verwendete Netz, unüberwacht! Rückgekoppelte (rekurrente) Netze: • Rückgekoppelte Netze sind dynamisch, sie können, müssen aber nicht konvergieren. • Konvergiert das Netz nicht, können Periodika oder Attraktoren auftreten. Jordannetze Ein Jordannetz ist aufgebaut wie ein MultilayerPerzeptron, hat jedoch für die Neuronen der Ausgabeschicht zusätzliche Kontextneuronen k1,..,kk, die einen Output des Netzes zwischenspeichern (puffern) und im nächsten Zeitschritt wieder ins Netz einbringen: Kontextneuron Radiale Basisfunktionennetze • RBF-Netze sind dreischichtige FeedForward-Netze, deren Schichten vollständig miteinander verknüpft sind • Sie dienen wie die MLPs als Funktionsapproximatoren, d.h. sie können eine unbekannte Funktion nach dem Training simulieren Der Aufbau von RBF-Netzen Ein RBF-Netz besteht aus • Eingabeneuronen, diese sind wie beim Perzeptron Identitätsneuronen • Ungewichteten Verbindungen zwischen Eingabe- und versteckter Schicht • Informationsverarbeitenden Neuronen in der versteckten Schicht, sog. RBF-Neuronen h1,...,hk mit Zentren c1,...,ck • Einer zu trainierenden Gewichtsschicht • Einer Schicht Ausgabeneuronen 1,...,k, die als Inputfunktion die gewichtete Summe haben und diese identisch ausgeben Das RBF-Neuron Beim RBF-Neuron verwendet man den Euklidischen Abstand zwischen dem Eingabevektor e und dem Zentrum ch des RBF-Neurons h als Propagierungsfunktion: rh fin e e ch e c i h , i 2 iI Das RBF-Neuron 2 Dieser Abstand wird dann durch die Aktivierungsfunktion des RBF-Neurons, eine Gauß-Funktion, geschickt: f act rh e rh 2 2 2 h Das Training von RBF-Netzen Es wird die Delta-Regel angewendet (wobei keine Backpropagation nötig ist, da nur eine Gewichtsschicht trainiert wird). Die Funktionsapproximation Die Funktionsapproximation Trainierte RBF-Netze können durch das Aufsummieren von Gaußglocken eine Funktion annähern und simulieren. Vergleich: RBF-Netze und MLPs Ob ein Problem einfacher von einem RBF-Netz oder von einem MLP, das mit Backpropagation trainiert wird, gelöst werden kann, hängt von den zu klassifizierenden Clustern ab: Klassifikation durch ein Radiales Basisfunktionennetz Klassifikation durch ein Multilayer-Perzeptron Hopfieldnetze Hopfieldnetze sind unüberwacht lernende Neuronale Netze, die zur Mustererkennung eingesetzt werden. Sie sind physikalisch motiviert: • Elementarmagnete (Neuronen) beeinflussen sich gegenseitig • Sie drehen sich dabei auf der Suche nach dem energetisch günstigsten Zustand (Minimum der Energiefunktion) • Es werden zwei Drehwinkel, sog. Spins zugelassen Der Aufbau eines Hopfieldnetzes Ein Hopfieldnetz Die binäre Schwellenwertfunktion • Ein Hopfieldnetz besteht aus einer Menge K von Neuronen, die untereinander vollverknüpft sind. Es gibt keine Aufteilung in Neuronenschichten! • Die Aktivierungsfunktion der Neuronen ist die binäre Schwellenwertfunktion mit den Ausgaben 1 oder -1. • Die Verbindungen zwischen den Neuronen sind symmetrisch gewichtet, es gilt also wi,j=wj,i . • Der Zustand des Netzes ist die Gesamtheit der Aktivierungen aller Neuronen; er wird als Vektor (Binärstring) geschrieben: z 1,1K . Wie arbeitet ein Hopfieldnetz? • Die Initialisierung aller Neuronen durch K einen Vektor x 1,1 wird als Eingabe in das Netz bezeichnet. • Das Hopfieldnetz konvergiert immer (bewiesen). • Wenn das Netz seinen Zustand nicht mehr ändert, ist der neue Netzzustand K y 1 , 1 . die Ausgabe des Netzes: Zustandwechsel der Neuronen In jedem Zeitschritt wird zufällig das Neuron ausgewählt, das als nächstes seinen Zustand ändern soll. Der neue Zustand eines Neurons i wird wie folgt berechnet: xi t f act wi , j x j t 1 jK Binäre Schwellenwertfunktion: falls neti 0 1, f act neti 1, sonst Frage Welchen Einfluss hat das Vorzeichen des Gewichtes wi,j auf den Aktivierungszustand des Neurons i , abhängig vom Aktivierungszustand des Neurons j ? xi t f act wi , j x j t 1 jK Das Training von Hopfieldnetzen • Das Netz wird mit jedem Trainingsmuster p 1,1 genau einmal initialisiert • Sind zwei Neuronen i,j in dem gleichen Zustand, so wird 1 zu dem Gewicht wi,j addiert, andernfalls wird 1 subtrahiert. Die Lernregel lautet also K wi , j pi p j pP Ein hohes positives Gewicht bedeutet soviel wie: „In den Trainingsdaten haben Neuron i und j oft den gleichen Zustand.“ Leider kann ein Hopfieldnetz auf diese Art nur begrenzt P MAX 0.139 K viele Muster speichern, es gilt: Frage • Wie viele Neuronen braucht man etwa, um 10 Trainingsmuster in einem Hopfieldnetz abzuspeichern? • Was könnte passieren, wenn die Anzahl der maximal speicherbaren Trainingsmuster überschritten wird? Hopfieldnetze als Autoassoziatoren Ein Autoassoziator a hat folgende Eigenschaften: • Bei Eingabe eines bekannten Musters wird genau dieses wieder ausgegeben a p p Trainingsbeispiele mit je 10x12 binären Pixeln • Auch bei verrauschten Daten, die nahe an einem bekannten Muster liegen, erzeugt das Netz die gleiche Ausgabe a p p Konvergenz des Netzes bei Eingabe einer stark verrauschten 3 Aufgabe 6 Berechne die Gewichte wi,j für ein Hopfieldnetz mit 6 Neuronen unter Verwendung der folgenden Trainingsmenge: P 1,1,1,1,1,1 ; 1,1,1,1,1,1; 1,1,1,1,1,1 Trage die Gewichte in eine solche Tabelle (also eine Matrix) ein: 1 2 3 4 5 6 1 0 2 3 4 5 6 0 0 0 0 0 Self Organizing Maps (SOMs) SOMs, auch Kohonenkarten genannt (nach Teuvo Kohonen), sind unüberwacht lernende Neuronale Netze, die biologische Eigenschaften des Gehirns realisieren: • Das Gehirn reagiert auf Reize (Inputs) mit Zustandsänderungen. • Es interessiert oft nicht, wie stark ein Neuron feuert, sondern lediglich welches Neuron aktiv ist. • Bei ähnlichen Reizen werden Neuronen benachbarter Regionen aktiviert. • Hochdimensionale Eingabewerte müssen auf weniger Dimensionen abgebildet werden. Das Konzept der selbstorganisiernden Karten SOMs arbeiten in zwei Datenräumen: • Dem N-dimensionalen Eingaberaum • und dem G-dimensionalen Gitter, auf dem die Neuronen liegen. Ziel ist es, den höherdimensionalen Eingaberaum auf Bereiche in dem Gitter abzubilden, man sagt auch: eine Karte von ihm zu zeichnen. Dazu erhält die SOM Punkte aus dem Eingaberaum und versucht, diese Punkte abzudecken, indem jedem Neuron ein Bereich aus dem Eingaberaum zugeordnet wird. Der Aufbau von SOMs • Eine SOM besteht aus einer Menge von Neuronen k1,…,kk • Jedes SOM-Neuron hat ein Zentrum ck im Eingaberaum, das beim Training angepasst wird • Diese Neuronen haben untereinander Nachbarschaftsbeziehungen, die durch sogenannte Topologiefunktionen definiert sind. Beispieltopologien Die Arbeitsweise einer SOM Eine fertig trainierte SOM arbeitet in diesen Schritten: 1. 2. 3. ! Eingabe eines beliebigen Wertes x aus dem Eingaberaum Abstandsberechnung von jedem Neuron k zu x: x ck Aktivierung des Neurons i (Gewinnerneuron) mit dem geringsten Abstand (auch Winner-takes-all-Schema genannt) Die Ausgabe, die uns interessiert ist nicht, wie hoch die Aktivierung dieses Neurons ist, sondern nur welches Neuron aktiv ist ! Das Training von SOMs 1. 1. 2. 3. Initialisierung: Die Neuronenzentren ck werden zufällig gewählt Anlegen eines Eingangsmusters: Ein Punkt aus dem Eingaberaum wird in das Netz eingegeben Abstandsmessung: Es wird für jedes Neuron k der Abstand p ck bestimmt. „Winner-takes-all“: Das Gewinnerneuron i wird ermittelt, für das gilt: p ci p ck 4. p k i Adaption der Zentren: Die Zentren werden nach der SOM-Lernregel angepasst… Ein eindimensionales Gitter (rechts dargestellt) in einem zweidimensionalen Eingaberaum: Die Zentren des Gewinnerneurons 3 und seiner Nachbarn 2 und 4 werden in Richtung der Eingabe p verschoben. Beispielhaftes Verhalten einer SOM mit eindimensionaler Topologie und zweidimensionalem Eingaberaum: 0 Eingabemuster 300 Eingabemuster 100 Eingabemuster 500 Eingabemuster 5000 Eingabemuster 70000 Eingabemuster 50000 Eingabemuster 80000 Eingabemuster Reinforcement Learning Beim Reinforcement Learning (bestärkenden Lernen) handelt es sich um einen Mittelweg zwischen überwachtem und unüberwachtem Lernen. Die Idee: • Ein Agent wechselwirkt mit einem Umweltsystem, das ihm positive oder negative Rückmeldungen (Rewards) liefert • Ziel: Das Finden einer Strategie (Policy), die zu jeder Situation die Summe der erwarteten zukünftigen Rewards maximiert. Lernen durch Ausprobieren und durch „Zuckerbrot und Peitsche“ Ein Beispiel • Agent: sich in vier mögliche Richtungen im Gitter bewegender Punkt • Umweltsystem: diskrete Gitterwelt (Gridworld) mit 5x7 Feldern • Die dunklen Felder sind nicht begehbar. • Das blaue Feld ist eine Tür, die zufällig entweder offen oder geschlossen ist: das System ist nicht deterministisch. • Zustände/ Situationen: die 30 (bzw. bei geschlossener Tür 29) Felder, die der Agent belegen kann • Aktionen: Der Agent geht je ein Feld nach oben, unten, rechts oder links. • Ziel: Der Agent erreicht den Ausgang (hellblau). Standard-Reward-Vergaben • Pure Delayed Reward: Die Belohnung wird erst am Schluss vergeben rt 0 t bei Gewinn : r 1 bei Verlust : r 1 • Pure Negative Reward: „Je schneller, desto besser“, jede Aktion wird bestraft rt 1 t • Avoidance Strategy: Schädlichen Situationen wird ausgewichen: 1, bei schädliche n Situatione n , rt 0, sonst . Frage Welche Arten der Reward-Vergabe sind für die folgenden Aufgaben am besten geeignet? 1. Der Agent soll in der Gitterwelt möglichst schnell aus einem Labyrinth herausfinden. 2. Der Agent soll ein Spiel, beispielsweise „Tic Tac Toe“, erlernen. 3. Der Agent soll in der Gitterwelt den Hindernissen ausweichen. Der Return Die aufsummierten Rewards werden als Return Rt bezeichnet. Rt rt 1 rt 2 ... r Bei unendlich langen Folgen werden weit in der Zukunft liegende Rewards schwächer gewichtet: Rt rt 1 1rt 11 2 rt 1 2 ... k rt k (0 1) x 0 Der optimale Return in der Beispiel-Gridworld (unter Verwendung des pure negative Rewards) Die optimale Policy Die optimale Policy soll den Return langfristig maximieren. Um zu einer optimalen Policy zu gelangen, muss der Agent seine Situation und seine Aktionen beurteilen können. Es gibt daher -die State-Value-Funktion zur Situationsbewertung -und die Action-Value-Funktion zur Aktionsbewertung. Die State-Value-Funktion Die State-Value-Funktion bewertet eine Situation, indem sie den Erwartungswert des Returns liefert. Einfaches Beispiel Tür auf Tür öffnet mit Wahrscheinlichkeit 1/2 Die Action-Value-Funktion • Die Action-Value-Funktion bewertet eine bestimmte Aktion unter einer bestimmten Situation. Beispielhafte Action-ValueWerte in unserer Gridworld …und was hat Reinforcement Learning mit Neuronalen Netzen zu tun? • Die State-Value-Funktion und die Action-Value-Funktion sind oft so komplex (bei einem Backgammon-Spiel 1020 mögliche Situationen), dass sie angenähert werden müssen • Zur Approximation dieser Funktionen werden überwacht lernende Neuronale Netzealso MLPs oder RBF-Netzeeingesetzt Java-Applets Auf dieser Seite findet ihr Programme von InformatikStudenten der Universität Bonn zu den verschiedenen Arten künstlicher Neuronaler Netze: http://www.nero.uni-bonn.de/course/courseframe.html Viel Spaß beim Ausprobieren! „Wenn das Gehirn so einfach wäre, dass wir es verstehen könnten, wären wir zu dumm, um es zu begreifen.“ (Jostein Gaarder)