Kein Folientitel
Werbung

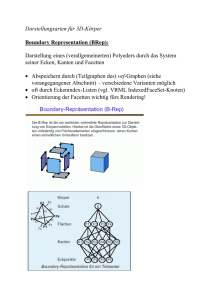
Graphische Datenverarbeitung III Dr. Markus Heitz Modellierung Geometrie • Beschreibt die räumliche Position der Elemente im Raum (ohne den Zusammenhang zwischen den Elementen zu registrieren). Topologie • Beschreibt die Gemeinsamkeiten zwischen Elementen, die einen Körper beschreiben. • Es gibt topologische Regeln, die immer erfüllt sein müssen, damit ein Volumen „richtig“ ist, • Beispiel: Es können nicht mehr als 2 Flächen oder Körper an eine Kante stoßen. (Würfel: 3 Nachbarpunkte, 3 Nachbarkanten, 3 Nachbarflächen) Geometrische Grundelemente • Die kleinsten, unteilbaren graphischen Objekte werden graphische Primitive genannt: • Punkt, Gerade, Kreis, • Kreisbogen, Ellipsenbogen, • Freiformkurven • Buchstaben, Text, Bemaßung, Symbole, • Linienzug (Rechteck, Dreieck, Polygon), • Punktmengen (pixel array), • Ebene, Fläche • Kugel, Zylinder, Quader, etc. Geometrische Grundelemente II • Graphische Objekte werden aus Primitiven zusammengesetzt. • Basisdatentyp für alle graphischen Primitive ist der Punkt in einem 2D- oder 3D-Koordinatensystem. • Die Beschreibungen eines Objektes durch Primitive ist nicht eindeutig; die Wahl der Primitive orientiert sich an der graphischen Anwendung. Die wichtigsten Randbedingungen sind Rechenzeit und Speicherbedarf. • Bei der graphischen Ausgabe wird in den meisten Fällen eine Abbildung auf niedrigere Strukturen erfolgen: Kreis als Folge von Geraden, Gerade als Folge von Punkten (Pixeln). Datenstrukturen • Die Datenstrukturen sind abhängig von der Funktionalität – passiv – interaktiv – 2D – 3D • Anforderungen des Anwendungsprogramms – Genauigkeit – Art der Ausgabe – Geschwindigkeit • Häufig sind mehrere Datenstrukturen vorhanden, um den unterschiedlichen Anforderungen zu entsprechen: – Datenstruktur des Anwendungssystems – Datenstruktur des Graphiksystems – Datenstruktur der graphischen Ein- / Ausgabegeräte Struktur der Speicherbelegung • • • • • • Betriebssystem Graphik-Bibliothek Anwendungs-Programm (z.B. CAD) Makro-Programm Modell-Datenstruktur Display-Datenstruktur Mod ell-Daten struktur Feedback Selektion Dis play-Datenstru ktur Feedback Bildschirm Modell-Datenstruktur • 2D- Modelle: – lineare Modelle: Bilder aus Punkten, Linien, Kreise zusammengesetzt – areale Modelle: Bild aus Bildpunkten und kleinen Flächen zusammengesetzt • 3D- Modelle: – Draht-/Kantenmodelle: wie lineare 2D-Modelle – Flächenmodell: Ebenen, kugelförmige (elliptische) Flächen, Torus, Freiformflächen. Wichtig: Die Berandung einer Fläche entsteht durch Schnitte mit anderen Flächen. Ein Objekt wird also durch die Gleichungen der Flächen und durch deren Berandungslinien definiert. – Volumenmodelle: Boundary-Representation (B-Rep), Constructive Solid Geometry (CSG), Zellenzerlegung (3D-Pixel: Voxel) Datenverwaltung • Direktzugriff: Adresse bekannt oder berechenbar (z. B. Feld, Hash-Tabelle) • sequentiell • mit Zeigerlisten • Hierarchie: Hierarchische Struktur eines Tetraeders Für das dynamische Verändern von graphischen Daten sind verkettete Listen gut geeignet Quadtrees und Octrees • Quadtrees und Octrees: Eine wichtige Methode für die Speicherung graphischer Objekte. • 2D: Quadtrees • 3D: Octrees. • Verallgemeinerung von Binärbäumen. • Die Abbildungsebene wird in Quadranten unterteilt. • Liegt in einem der vier Quadranten ein Objekt, so wird am Referenzpunkt des Objekts beginnend eine weitere Unterteilung des Quadranten in wiederum vier rechteckige Teile vorgenommen. • Es ergibt sich automatisch eine hierarchische Struktur (Beispiel in der PP-Präsentation). Speicherung von Punkten in einer Quadtree-Liste P 2 P 3 P 4 P 1 P1 P P 2 3 P 4 • Liegt ein Punkt auf einer Achse, so wird er dem Quadranten zugeordnet, der der nächste im Uhrzeigersinn ist. Schnitte bei Draht-, Flächen- und Volumenmodelle Drahtmodell Volumenmodell Flächenmodell Kanten-/Drahtmodelle (wire frame) • Das graphische Objekt wird ausschließlich durch seine Eckpunkte und deren Verbindung untereinander als ein Netzwerk von Knoten und Kanten repräsentiert. • Niedrige Datenhaltung • Schnelle Antwortzeiten • Verwendung in CAD-Systemen für Eingabe, schnelle Darstellung. • Nachteile: – fehlende Unterscheidungsmöglichkeit zwischen dem Inneren und dem Äußeren des Objektes. – Flächen und Volumen des Objektes nicht definiert. – Schnitte durch den Körper sind nicht möglich. – Bei komplexen Objekten unübersichtlich. Flächenmodelle • Flächen sind in der Regel relativ einfach analytisch zu beschreiben, z.B. rotationssymmetrische Körper, die beim Drehen entstehen. • Flächen, die nicht analytisch beschrieben werden können (Freiformflächen), lassen sich durch Flächensegmente approximieren. • Geringerer Rechenaufwand im Vergleich zu volumenorientierten Systemen geringerer Rechenaufwand. • Zusätzlich zur Flächenbeschreibung ist noch die Information notwendig, auf welcher Seite sich das Volumen anschließt (in OpenGl durch Drehsinn) Volumenmodelle • Drei unterschiedliche Verfahren – flächenorientiertes Modell: boundary representation model (BREP), – volumenorientiertes Modell: constructive solid geometry (CSG) – Raumzerlegung: spatial occupancy enumeration (SOE), 'Voxel'-Modelle, 'Octree'-Modelle Constructive Solid Geometry (CSG) • Erstes System: PADL-Modellierer von Anstides Requicha, Universität von Rochester. • Definition des Modells durch Objekt-Primitive (Zylinder, Würfel, Torus) • Operationen zum Kombinieren von Primitiven. • Die Modelldaten: Aufzeichnung der jeweils gewählten Primitiven und der damit vorgenommenen Operationen. • während sämtlicher Konstruktionsphasen im nicht-ausgewerteten Zustand. • Immer wenn eine bildliche Darstellung des Modells benötigt wird, müssen die aktuellen Ränder neu berechnet werden. Boundary Representation Model (BREP) • Ian Braid, Universität Cambridge. • Definition des Modells ebenfalls durch Kombination von Primitiven. • Datenmodell: Beschreibung der Oberflächengeometrie. • Zu jedem Zeitpunkt ist ein ausgewertetes Modell verfügbar. • CSG und BREP unterscheiden sich durch das Datenmodell, gleiche Art der Eingabe. Spatial Occupancy Enumeration (SOE) • Wird auch als "Spatial Subdivision"-Verfahren, Zellenzerlegungsmodell oder als „Octree“-Methode bezeichnet. • Das Modell wird durch "Voxel" (3D-Pixel) unterschiedlicher Größe repräsentiert • Octree-Datenstruktur • Geringere Genauigkeit, daher nicht geeignet für MaschinenbauAnwendungen. • Für Visualisierungen geeignet • Hoher Speicherbedarf: Verfahren wird wegen billigerem Speicher immer wichtiger. Boolsche Operationen mit Primitiven Vereinigung RD Differenz R-D Durchschnitt RD Erstellen eines Volumenmodells mit CSG Datenstruktur des Modells CSG • Nachteil: Aufwendige Eingabe der absoluten Koordinaten und Vektoren, die die Positionen der Primitiven vorgeben. • Daher meist komfortablere Eingabemethoden: – Es werden zweidimensionale Profile definiert und diese mit Hilfe von Pseudo-Booleschen Operationen wie z. B. "Extrudieren", "Fräsen" oder "Stanzen", in ein dreidimensionales Gebilde transformiert. – Die Eingabe wird in internes CSG-Datenmodell umgewandelt. BREP • Die Umrandung eines Festkörpers besteht aus drei Elementen: Flächen, Kanten und Ecken. • Topologie: Beschreibung der Verknüpfungen dieser Elemente. • Beispiel Pyramide: 5 Ecken, davon eine mit mit 4 Kanten und 4 mit drei Kanten. • Beispiel Würfel: 8 Ecken mit jeweils 3 Kanten. • Topologische Beschreibung besagt nichts über die räumliche Anordnung der einzelnen Elemente, zusätzliche geometrische Informationen für vollständige Beschreibung notwendig. • Beispiel: Topologische Regeln: Euler • Euler (1707 bis 1783), Regeln für konvexe Polyeder: E + F - K = 2 mit E = Anzahl der Ecken (Punkten) F = Anzahl der Flächen K = Anzahl der Kanten • Beispiele: – Quader: 8 + 6 -12 = 2 – Bei Zylinder, Kegel und Kugel wird eine Hilfslinie zur Definition von Punkten und Kanten benutzt. – Zylinder: 2 + 3 - 3 = 2 – Kegel: 2+2-2=2 – Kugel: 1+2-1=2 Topologische Regeln: Poincaré • Poincaré (1854 bis 1912), Erweiterung auf Objekte mit Löchern, internen Höhlungen und Durchbrüchen (Durchbohrungen), zusammengesetzte Körper: E + F - K = 2 (1 + H - D ) + L L = Anzahl der Löcher D = Anzahl der Durchbrüche H = Anzahl der Höhlungen Loch Durchbruch Höhlung Topologische Regeln • Loch: eine Schleife von Kanten, die nicht mit der Hauptschleife verbunden ist. • Wenn ein modelliertes Objekt nicht dieser Regel entspricht, bedeutet dies, daß es auch nicht herstellbar ist. • Umgekehrt folgt aus der Tatsache, daß ein modelliertes Objekt dieser Regel entspricht, nicht notwendigerweise, daß es auch herstellbar ist. – Regel nicht erfüllt -> Körper falsch ! – Regel erfüllt -> Körper kann richtig oder falsch sein ! • BREP-Modellierer führen zusätzliche Tests durch: – nicht mehr als zwei Flächen grenzen an eine Kante – jede Kante wird durch genau zwei Ecken begrenzt – jede Fläche wird durch einen geschlossenen Kantenzug begrenzt SOE: Das Octree - Modell • Der Objektraum wird in 8 gleichgroße Quader unterteilt. Jeder Quader wird untersucht, ob er leer, ganz gefüllt oder partiell gefüllt ist. Alle partiell gefüllten werden wiederum in 8 gleichgroße Quader unterteilt, usw.. Es entsteht ein Octree. • Vorteile: – räumlich adressierbar – räumlich eindeutig – bei ausreichendem Speicher sehr schnelle Visualisierung möglich • Nachteile: – – – – keine expliziten Relationen zwischen den Teilen eines Objekts keine Attribute für Flächen, Kanten angebbar extrem speicherintensiv Information über die Art der Flächen (planar, gekrümmt) fehlt, deshalb für Bearbeitungsvorgänge nicht brauchbar. Vergleich zwischen CSG und BREP I • "Größe" der Datenstruktur: CSG-Datenstrukturen sind "kompakter" als BREP-Datenstrukturen. • Validität des Modells: CSG-Modelle werden grundsätzlich nur durch gültige Operationen aus gültigen Primitiven erzeugt. • Rückverfolgbarkeit der Entstehungsgeschichte: – Eine CSG-Datenstruktur repräsentiert die gesamte Entstehungsgeschichte des Modells. Editieren einzelner Entwurfsschritte möglich. – Bei BREP wird immer die im Augenblick vorliegende Datenstruktur modifiziert. Vergleich zwischen CSG und BREP II • Verarbeitungszeit: CSG-Systeme erfordern ständige Neuauswertung. Aber: auch bei bei BREP-Modellierern steigt die Verarbeitungszeit mit zunehmender Komplexität der topologischen Struktur. • Entwurfsmodifikation auf höherer Ebene: Anwender benutzt Boolesche Operationen nicht direkt. Bei BREP-Modellierern kann die Geometrie eines Objekts in einfacher Weise verändert werden, sofern die Topologie dabei erhalten bleibt. Mehrdeutigkeiten bei CSG-Darstellungen Bearbeiten von Flächen • Ein BREP-Modellierer stellt die Körperumrandung intern so dar, wie der Benutzer des Systems sie sieht. Alle Kanten, Flächen und Ecken lassen sich direkt bearbeiten. • Toleranzen oder Oberflächen-Finish lassen sich leicht hinzufügen. • CSG: Hinzufügen durch weitere boolsche Operationen möglich. Geometrische Genauigkeit • Real-Zahlen doppelter Genauigkeit (64 Bit): 14 signifikante Dezimalstellen. • Nach numerischen Fehlern: ca. 11 oder 12 Stellen, je nach Algorithmus. • Beispiel: Mechanische Bauteile müssen wenigstens auf 0,01 mm genau definiert werden. Bei einem Gesamtobjekt in der Größenordnung 10 m werden 6 Stellen benötigt. Realistische Darstellung (Rendering) • Liniengraphik – schnell, Echtzeit – für CAD und Modellierer – Verdeckunsalgorithmen zur besseren Übersichtlichkeit • Schattierte Flächendarstellung – langsamer, keine Echtzeit – Ziel: photorealistische Darstellung – Methoden: Shading, Ray Tracing, Radiosity Shading und Lighting: Beleuchtungsmodelle • Geometrischen Abhängigkeiten zwischen Objekt, Lichtquelle und Betrachter. • Beispiel: Einfallswinkel des Lichtes auf eine Körperoberfläche beeinflußt die Helligkeit. • Schattierungsverfahren: Bestimmung der Intensitäten der einzelnen Pixel innerhalb eines Bildes durch Anwendung eines Beleuchtungsmodells (z.B. bei mehreren Lichtquellen). – Lokales Beleuchtungsmodell: lokaler Lichteinfall bezüglich eines Objekts – Globales Beleuchtungsmodell: lokaler Lichteinfall und Interreflexionen zwischen mehreren Objekten. Lichteinfall und Helligkeit • Helligkeit einer Fläche: I = ka Ia + kd Id + ks Is • Ia: Ambiente Beleuchtung (Hintergrundlicht), damit im Schatten liegende Flächen nicht völlig schwarz sind (in der Regel 10% Helligkeit) • Id: Diffuse Reflexion (Streuung) einer Lichtquelle, bestimmt die Farbe des Objekts. • Is: Spekulare Reflexion einer Lichtquelle (Glanzlichter) • Vereinfachtes Reflexionsmodell simuliert physikalischen Vorgang. Diffuse Reflexion • Beleuchtet eine Lichtquelle der Lichtstärke Ip eine Fläche im Abstand r unter dem Winkel f (bezüglich der Flächennormalen), so ergibt sich folgende Beleuchtungsstärke auf der Fläche (Lambertscher Cosinus): Id Ip r2 cos F • Für andere F ist I = 0 • Hängt nicht vom Betrachtungswinkel ab mit -p/2 < F < p/2 Spekulare Reflexion • Ideale Reflexion: Einfallswinkel = Ausfallswinkel • Spekulare Reflexion: Is Ip r 2 cos W n W: Winkel zwischen Blickrichtung und Spiegelrichtung. n: Materialeigenschaft Spiegelnde Streuung Ideale Reflexion Diffuse Streuung Schattierung, Gouraud- und Phong-Shading • Jede Fläche wird durch polygonale Flächenstücke approximiert, für die die Shadingfunktion einmal errechnet wird. Dadurch entsteht ein facettenartiges Aussehen. • Der Facettengenerator baut inkrementell eine facettierte Darstellung der Geometrie für jeden Konstruktionsschritt auf und legt die Daten im Facettengeometriemodell ab. • Die Feinheit der Facettierung wird aus Rechenzeitgründen durch den Benutzer nach Bedarf eingestellt. • Durch Interpolation der Intensitäten über die Facette kann der optische Eindruck bei nur leicht ansteigender Rechenzeit stark verbessert: Gouraud Shading • Interpolation der Flächennormalen: Phong Shading Shading Gouraud Shading • Berechnung der Intensitäten an den Eckpunkten anhand der Flächennormalen • Lineare Interpolation der Intensitäten in der Fläche der Facette • Spiegelnde Reflexion kaum simulierbar (Glanzlichter werden nicht korrekt dargestellt) Phong Shading • Interpolation der Flächennormalen und nicht der Intensitäten • Bessere Darstellung von Reflexion • Höhere Rechenzeit Teekessel von Utah Flat Shading Gouroud Shading Phong Shading Effiziente Visualisierung • Culling: Verfahren zur Unterdrückung von Geometrien für die Grafikpipeline. • Backface Culling: Rückseiten von Flächen werden nicht gezeichnet. • Viewfrustrum-Culling: Flächen außerhalb des sichtbaren Pyramidenstumpfs (oder Quaders) werden nicht gezeichnet. • Occlusion Culling: Verdeckte Geometrien werden entfernt. Besonders wichtig bei CAD-Modellen (z.B. Details im Innern eines Modells entfernen bei Außenansicht) • Tessilierung: Verringern der Anzahl der Dreiecke ohne die optische Qualität wesentlich zu verschlechtern. Tessilierung I • Sehnenfehler (die Höhe zwischen einem Bogen und einer Sehne) als Steuervariable für die Tesselierung. Beispiele: RossignacSimplify- und der Successive-Relaxation-Algorithmus (SRA). • Geometrien werden nach verschiedenen Kriterien zusammengefasst. • Alternative: Ansichtsabhängige Reduktion. Tessilierung II • Ein Level-of-Detail- (LOD-)Knoten wählt eine Darstellungsvariante danach aus, wie weit das zu visualisierende Objekt vom Kamerapunkt entfernt ist. Je größer der Abstand, desto weniger Details sind zu sehen. Effiziente Visualisierung: Tri-Fans, Tri-Strips • TriFans oder TriTrips sorgen für eine optimale Darstellung zusammenhängender Dreiecke. • Es wird wird mit Ausnahme des ersten Dreiecks nur ein Koordinatenpunkt in Bildschirmebene transformiert. • n Dreiecke: n+2 Transformationen • Optimale Nutzung der Grafik-Pipeline • Alle Flächengeometrien in TriFans oder TriStrips umgwandeln. Funktionen moderner 3D-Graphikeinheiten I • Alpha Blending: Darstellung von Transparenz durch zusätzlichen Alpha-Kanal zu RGB hinzugefügt: RGBA. In Spielen wird häufig RGBA 4444 verwendet. • Bilineares Filtern: Tiefpaßfilter, der scharfe Übergänge verwischt: Weichzeichner. Sinnvoll, wenn Texturen stark vergrößert werden. Die zusätzlichen Bildpunkte werden nicht einfach kopiert sondern interpoliert. • Bump-Mapping: Die glatte Oberfläche wird mit „Bumps“ verziert, d.h. sie erscheint nicht mehr geometrisch perfekt und damit wie im richtigen Leben. • Color-Key: Eine bestimmte Farbe wird als transparent definiert und ersetzt das Alpha-Blending. Hintergrund kommt zum Vorschein. Schneller als Alpha-Blending. Funktionen moderner 3D-Graphikeinheiten II • Environment Mapping: „bildet die Umwelt“ ab und simuliert dadurch reflektierende Oberflächen. Beispiel: Im Fenster eines fahrenden Autos spiegeln sich Wolken und vorüberziehende Häuser. • Fogging: der Hintergrund verschwindet im Dunst, weit entfernte Objekte müssen nicht mehr dargestellt werden. Verstärkt den Tiefeneindruck einer 3D-Szene. • Lens Flaring: Nachahmung von Lichtreflexen durch Photoobjektiv, Frontscheibe eines Autos etc... Funktionen moderner 3D-Graphikeinheiten III • Mip-Mapping: Mip = ‚multum in parvo‘ = ‚vieles im Kleinen‘ Texturen werden in verschiedenen Auflösungen verwendet. Weniger Fehler, störende Muster entfallen weitgehend. • Perspektivische Korrektur: Texturen wirken auf Gegenständen, die sich vom Vorder- in den Hintergrund erstrecken, unrealistisch. Die rechenaufwendige perspektivische Korrektur skaliert die Texturen: vorne groß, hinten klein. • Schattenbildung: Simulation eines Schattens durch Projektion von Objekten auf ebene Flächen. In Shading-Modellen kommt sonst kein Schatten vor.