PowerPoint-Präsentation
Werbung

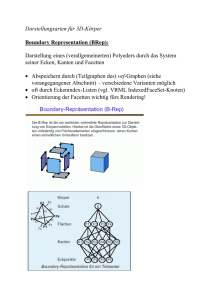
Seminar zur Geoinformation Implementation von 3D Objekten Referent: Betreuer: Alexander Linke Dr. rer. nat. Thomas H. Kolbe Motivation Anwendungen für die Implementation 3 dimensionaler Objekte: 1. Robotertechnik 2. Simulation physikalischer Mechanismen 3. Immersive Systeme 4. CAD 5. GIS Anforderungen an Objekte Vorraussetzungen: 1. Unterscheidung zwischen Innen und Aussen 2. Oberflächeninformationen Darstellungsmöglichkeiten Eine geeignete Repräsentationsmethode muss den folgenden Kriterien genügen: 1. Diversität Es müssen viele Klassen von Objekten dargestellt werden können 2. Eindeutigkeit Eine Darstellung darf nur auf einen Körper führen 3. Genauigkeit Vermeidung von Approximationen 4. Sicherheit Keine Möglichkeit sogenannte invalid solids zu konstruieren Darstellungsmöglichkeiten 5. Kompaktheit und Effizienz 6. Algorithmen Implementierung effizienter Algorithmen soll ermöglicht sein Erzeugung eines Modells, welche alle diese Eigenschaften in Sich vereinigt, ist nicht möglich. Kompromiss erforderlich Arbeiten mit dreidimensionalen Objekten Operatoren – Regularized Boolean Set Operations - Dienen zur Erstellung neuer solids aus bereits vorhandenen - 3D Eqivalent zur Mengenlehre - Regularized Boolean Set Operators liefern als Ergebnis immer einen valid solid - 3 Operationen: -Vereinigung (Union) -Differenz (Difference) -Schnittmenge (Intersection) Modelling Systems Primitive Instancing Sweep Representations Boundary Representations Constructive Solid Geometry Modelling Systems Primitive Instancing Funktionsweise: Modelliert wird mit Hilfe einfacher 3D Formen - Primitives Komplexere Körper werden mit Hilfe von Parametern realisiert Bsp.: Zahnrad Primitives: Zylinderscheibe Parameter: Dicke Durchmesser Durchmesser Drehpunkt Drehpunkt Anzahl der Zähne Modelling Systems Sweep Representations Funktionsweise: Eine 2 dimensionale Fläche wird entlang einer Trajektorie geführt. Der Überstrichene Raum ergibt den Körper Bsp.: Rechteck Lineare Bewegung in Richtung der Flächennormalen ergibt einen Quader Rotation um eine Kante der Ebene ergibt einen Zylinder Modelling Systems Boundary Representations Funktionsweise: B-Reps beschreiben Objekte über ihre Oberflächengrenzen. Die Primitive sind dabei: • Punkte (vertices) • Kanten (edeges) • Flächen (surfaces) Modelling Systems z Kante (P6,P7) y Fläche (P1,P2,P3,P4) X Punkt (x,y,z) Modelling Systems Möglichkeit der Speicherung Flächen und Kanten werden als Funktion ihrer Punkte abgelegt. Um Wiederholung der Punktkoordinaten zu vermeiden, werden diese in einer Liste abgelegt und die Punkte entsprechend indiziert. Modelling Systems Constructive Solid Geometry Funktionsweise: Modellierung von Körpern mit Hilfe von Primitives Die Primitives sind valid solids, geometrisch einfache Körper, Welche über Parameter für: Translation Rotation Ausdehnung Skalierung In eine erwünschte Form gebracht werden. Modelling Systems Manche Systeme erlauben auch Halbräume neben valid solids. Vorteil: Vermeidung von redundanten Informationen Nachteil: Das sich ergebende Objekt muss nicht mehr unbedingt ein valid solid sein Möglichkeit der Speicherung Objekt wird in einem sogenannten CSG-Tree abgespeichert Innere Knoten: Regularized Boolean Set Operators, Form-Parameter Blätter: simple primitives Ausgabe des Objekts Kombination der Eigenschaften der Blätter führt auf die EigenSchaften der Wurzel Vergleich zwischen CSG und B - Rep Kriterien für eine geeignete Repräsentationsmethode 1. Diversität 2. Eindeutigkeit 3. Genauigkeit 4. Sicherheit 5. Kompaktheit und Effizienz 6. Algorithmen Vergleich zwischen CSG und B - Rep 1. 2. Diversität a) B-Reps können eine weite Auswahl von Objekten darstellen. Die Auswahl kann jedoch durch Ausschliessen von curved surfaces erheblich reduziert werden b) CSG kann eine grosse Bandbreite Objekten darstellen Eindeutigkeit a) B-Reps teilen Objekte in einzelne Tiles auf. Daher sind sie nicht eindeutig b) CSG ermöglicht ebenfalls keine eindeutige Darstellung. Es gibt immer mehrere Wege, ein Objekt zusammenzusetzen Vergleich zwischen CSG und B - Rep 3. Genauigkeit a) B-Reps können geschwungene Oberflächen (curved surfaces) nur approximieren. b) 4. Genaue Darstellung erfordert hohen Rechenaufwand CSG ermöglicht eine akkurate Darstellung Sicherheit a) B-Reps sind für eine Validierung denkbar schlecht geeignet. b) Inkonsistenz der Datenstruktur der Punkte, Kanten und Flächen Flächen und Kannten können sich schneiden CSG ist einfach zu validieren Vergleich zwischen CSG und B - Rep 4. Sicherheit a) b) B-Reps sind für eine Validierung denkbar schlecht geeignet. Mögliche Inkonsistenz der Datenstruktur der Punkte, Kanten und Flächen Flächen und Kannten können sich schneiden CSG ist einfach zu validieren primitives sin valid solids regularized boolean set operators erzeugen nur valid solids nur die Syntax des CSG-Trees muss überprüft werden Vergleich zwischen CSG und B - Rep 5. Kompaktheit und Effizienz Unterscheidung zwischen berechneten (B-Rep) und nicht berechneten (CSG)Modellen. Unberechnete Modelle enthalten noch auszuwertende Informationen Berechnung vor der Durchführung einer Operation Berechnete Modelle sind bereits nach Durchführung einer Operation voll ausgewertet a) B-Reps können können sofort auf alle Informationen zugreifen Manche Operationen dauern jedoch erheblich länger (Bsp.: Punkt innerhalb Körper ?) b) Bei CSG muss der gesamte Tree bei jeder Berechnnung voll durchlaufen und ausgewertet werden. Boolean Operations und Transformationen können schnell aufgenommen werden Vergleich zwischen CSG und B - Rep 6. Algorithmen Sowohl für B-Reps als auch für CSG existieren effiziente Algorithmen um eine Darstellung von so kodierten Objekten zu erzeugen. Überführung der Modelle Constructive Solid Geometry Nicht möglich ! Boundary Representations Überführung der Modelle Umwandlung eines CSG Objekts in ein B-Rep Objekt Umwandlung erfolgt über die sukzessive Umwandlung der in den Blättern des CSG-Trees gespeicherten Primitives in Polyheder. Koordinaten der Punkte für das B-Rep Objekt sind in Form der die Primitives definierenden Parameter gespeichert. Man erhält dann die Punkte, Kannten und Flächen. Umwandlung eines B-Reps in ein CSG Objekt ist nicht möglich. CSG ist nicht eindeutig, ein Algorithmus hat keine Möglichkeit festzustellen, welche Anordnung die Richtige ist Überführung der Modelle Beispiel für die mangelnde Eindeutigkeit eines CSG Modells Berechnung von Boolean Set Operations 1. Hintergrund Ray Tracing Normalerweise angewandt für visible surface Operationen Vorgehenseise: -Wählen eines Projektionszentrums -zwischen Bild und P-Zentrum wird ein Gitter geschoben, Anzahl Maschen entspricht Anzahl Pixel Für jedes Pixel wird nun eine Gerade in Parameterform vom P-Zentrum in und durch das Bild gestreckt. Wird ein Objekt geschnitten, wird der Wert des Faktors t der Geradengleichung registriert. Man erhält 3D Informationen in 1D Schreibweise (entlang der Geraden) Berechnung von Boolean Set Operations Berechnung von Boolean Set Operations mittels Ray Tracing Methode Zum ersten Mal eingesetzt von Goldstein und Nagel Funktionsweise: -Aus einfachen Objekten per Boolean Set Operative produzierte Kombinationen werden ray traced. -Man erhält für jedes Objekt Werte für t für den Ein- und Austritt des Strahls. Jeder t Wert definiert den Beginn einer Strecke, in der der Strahl entweder innerhalb oder ausserhalb des Objekts ist. -Für jeden Strahl erfolgt einzeln die Berechnung der Boolean Set Operatives auf dem 1 D Strahl. -Eine Kombination von Objekten kann so in eine Überlagerung der Strecken umgewandelt werden, die der Strahl im Inneren der Objekte durchläuft Berechnung von Boolean Set Operations Kombination von Ray – Objekt Streckenlisten: Links Rechts t t L vereinigt mit R t t t t Berechnung von Boolean Set Operations Der Algorithmus durchwandert die CSG Hierarchie für jeden Strahl und wertet dabei die Schnittpunkt Knoten aus (ergeben sich aus den für t registrierten Werten) Funktion CSG Combine: -zwei Schnittpunktlisten, die nach aufsteigenden Werten für t geordnet sind -merging der Listen indem der Schnittpunktknoten mit dem nächst grösseren Wert für t herausgenommen wird. -der Status des Strahls wird (innen – aussen) wird durch Flags gesetzt -ob die Strecke an dem Schnittpunkt in dem combined Object verläuft wird durch eine Verknüpfungstabelle bestimmt. Berechnung von Boolean Set Operations Verknüpfungstabelle Links Innen Innen aussen aussen Rechts innen aussen innen aussen innen innen innen aussen innen aussen aussen aussen aussen innen aussen aussen Danke für ihre Aufmerksamkeit