ppt Version
Werbung

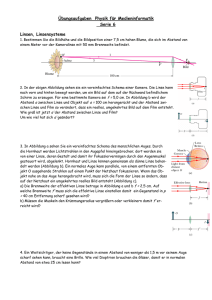
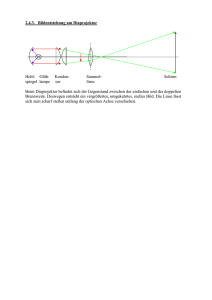
Linsenformen Sphärische sind von Kugelhauben begrenzt Konvexlinsen sammeln die Lichtbündel (Sammellinsen) Konkavlinsen zerstreuen die Lichtbündel (Zerstreuungslinsen) Hauptstrahlen durch eine Konvexlinse Beim Weg eines Lichtstrahls durch eine Linse finden zwei Brechungen statt. Mittelpunktstrahlen verlaufen durch dünne Linsen ohne Richtungsänderung Parallelstrahlen verlaufen nach der Brechung durch den Brennpunkt Brennpunktstrahlen werden nach der Brechung zu achsenparallelen Strahlen Hauptstrahlen durch eine Konkavlinse Beim Weg eines Lichtstrahls durch eine Linse finden zwei Brechungen statt. Mittelpunktstrahlen ändern beim Linsendurchgang ihre Richtung nicht Parallelstrahlen verlassen die Konkavlinse als divergente Strahlen. Brennpunktstrahlen: Auf den jenseitigen Brennpunkt gerichtete Strahlen verlaufen nach der Brechung achsenparallel Konvexe und konkave Linsen konvexe Linse konkave Linse Reelle und virtuelle Bilder Fall 1: Der Gegenstand ist außerhalb der doppelten Brennweite g 2 f Das Bild liegt bei f b 2 f Es ist umgekehrt, reell und verkleinert Fall 2: Der Gegenstand liegt zwischen der einfachen und der doppelten Brennweite f g 2 f Das Bild liegt bei b 2 f Es ist umgekehrt, reell und vergrößert Fall 3: Der Gegenstand ist bei oder innerhalb der einfachen Brennweite g f Das Bild liegt bei b<0 Es ist aufrecht, virtuell und vergrößert Vergrößerung Steht die Kerze zwischen Brennpunkt und Linse, kann man kein reelles Bild mehr auffangen. Schaut man jedoch von der rechten Seite her in die Linse, kann man ein aufrechtes vergrößertes Bild neben der Kerze sehen Brennweite Der Abstand der Brennpunkte F bzw. F’ nennt man die Brennweite f bzw. f’ Brechkraft/Brechwert: 1 D f Einheit der Brechkraft ist Dioptrien 1dpt=1/m Vergrößerungsgleichung Das Verhältnis von den beiden Entfernungen, bzw. Von der Bild- zur Gegenstandsgröße nennt man Abbildungsmaßstab : B b G g Abbildungsgleichung Die Herleitung der Abbildungsgleichung verläuft mit Hilfe ähnlicher Dreiecke (blau bzw. rot) und des Strahlensatzes. Für die blauen Dreiecke gilt: G/B=x/f Für die roten Dreiecke gilt: G/B=f’/x’ Will man die Brennweite f=f’ bestimmen, so benutzt man 1 1 1 f g b Fragen zu optischen Linsen 1. 2. Der Starfire-Refraktor der Sternwarte Eriskirch hat eine Brennweite von f=1802mm. Der Mond hat einen Durchmesser von G=3476km, seine Entfernung von der Erde beträgt g=384403km. a) In welcher Entfernung vom Objektiv entsteht das Bild? b) Welcher Durchmesser hat das Mondbild? Berechnen Sie für eine Linse mit der Brennweite f die Gegenstandsweite g, so daß die Bilder im Vergleich zum Gegenstand die Größen 1/100, 1/5, 1, 2, 5 und 100 haben.